【动手学深度学习v2】学习笔记03：线性回归、基础优化算法、线性回归实现

前文回顾：线性代数、矩阵计算、自动求导

文章目录

• 一、线性回归
• • 1.1 线性模型
  • 1.2 流程
  • • 1.2.1 损失函数
    • 1.2.2 训练数据
    • 1.2.3 参数学习
    • 1.2.4 显式解
  • 1.3 总结
• 二、基础优化算法
• • 2.1 梯度下降
  • 2.2 小批量随机梯度下降
  • 2.3 总结
• 三、线性回归的从零开始实现
• • 3.1 导入的库
  • 3.2 数据集
  • • 3.2.1 构造数据集
    • 3.2.2 展示数据集
  • 3.3 从零开始实现
  • • 3.3.1 生成小批量
    • 3.3.2 模型和初始化模型参数
    • 3.3.3 定义损失函数
    • 3.3.4 定义优化方法
    • 3.3.5 训练过程
    • 3.3.6 分析
• 四、线性回归的简洁实现
• • 4.1 用到的函数
  • 4.2 导入库并生成数据集
  • 4.3 读取数据
  • 4.4 模型的定义
  • 4.5 损失函数
  • 4.6 优化方法
  • 4.7 训练过程

一、线性回归

1.1 线性模型

给定n维输入 x ⃗ = [ x 1 , x 2 , ⋯   , w n ] T \vec{x}=[x_1, x_2, \cdots, w_n]^T x=[x1,x2,⋯,wn]T
线性模型有一个n维权重和一个标准偏差
w ⃗ = [ w 1 , w 2 , ⋯   , w n ] T , b \vec{w} = [w_1, w_2, \cdots, w_n]^T, \qquad b w=[w1,w2,⋯,wn]T,b输出时输入的加权和
y = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b y = w_1 x_1 + w_2 x_2 + \cdots + w_n x_n + b y=w1x1+w2x2+⋯+wnxn+b向量版本： y = ⟨ w ⃗ , x ⃗ ⟩ + b y=\langle \vec{w}, \vec{x} \rangle + b y=⟨w,x⟩+b

线性模型可以看做是单层神经网络。因为只有输入层和权重相关。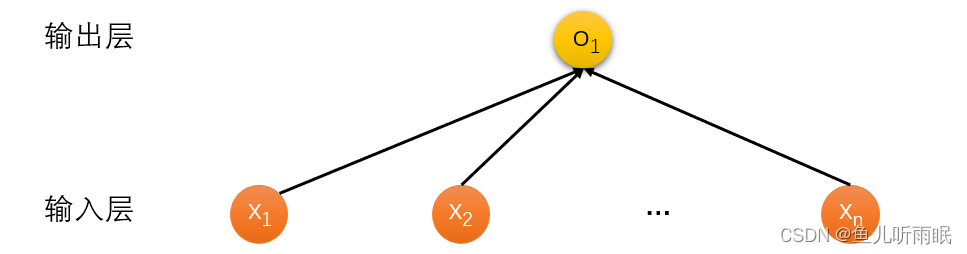

1.2 流程

1.2.1 损失函数

我们需要比较真实值和预估值，例如房屋售价和估价。
假设 y y y是真实值， y ^ \hat{y} y^是估计值，我们可以比较平方损失：
l ( y , y ^ ) = 1 2 ( y − y ^ ) 2 l(y, \hat{y})=\frac{1}{2}(y-\hat{y})^2 l(y,y^)=21(y−y^)2

1.2.2 训练数据

收集一些数据点来决定参数值（权重和偏差），例如过去6个月卖的房子。这些数据点称为训练数据，通常越多越好。
假设我们有n个样本，记
X = [ x 1 ⃗ , x 2 ⃗ , ⋯   , x n ⃗ ] T y ⃗ = [ y 1 , y 2 , ⋯   , y n ] T X = [\vec{x_1}, \vec{x_2}, \cdots, \vec{x_n}]^T \qquad \vec{y} = [y_1, y_2, \cdots , y_n]^T X=[x1,x2,⋯,xn]Ty=[y1,y2,⋯,yn]T

1.2.3 参数学习

训练损失
l ( X , y ⃗ , w ⃗ , b ) = 1 2 n ∑ i = 1 n ( y i − ⟨ x i ⃗ , w ⃗ ⟩ − b ) 2 = 1 2 n ∣ ∣ y ⃗ − X w ⃗ − b ∣ ∣ 2 l(X, \vec{y}, \vec{w}, b) = \frac{1}{2n}\sum_{i=1}^{n}(y_i-\langle \vec{x_i}, \vec{w} \rangle - b)^2 = \frac{1}{2n}||\vec{y} - X \vec{w} - b||^2 l(X,y,w,b)=2n1i=1∑n(yi−⟨xi,w⟩−b)2=2n1∣∣y−Xw−b∣∣2上式就是我们的损失函数了，我们的目标是找到值 w ⃗ , b \vec{w},b w,b 使损失函数值最小。
最小化损失来学习参数
w ⃗ ∗ , b ⃗ ∗ = a r g    m i n w ⃗ , b    l ( X , y ⃗ , w ⃗ , b ) \vec{w}^*, \vec{b}^* = arg\;\mathop{min}\limits_{\vec{w}, b}\;l(X, \vec{y}, \vec{w}, b) w∗,b∗=argw,bminl(X,y,w,b)

1.2.4 显式解

由于是线性模型，所以会有显式解。这也是唯一一个有最优解的模型，之后的所有模型都不会有最优解了。

首先，将偏差加入权重
X ← [ W , 1 ⃗ ] w ⃗ ← [ w ⃗ b ] X \leftarrow \begin{bmatrix}W, \vec{1}\end{bmatrix} \qquad \vec{w} \leftarrow \begin{bmatrix}\vec{w} \\ b\end{bmatrix} X←[W,1]w←[wb]将偏差加入权重之后，我们的预测就等于 X w ⃗ X\vec{w} Xw，即 y ^ = X w ⃗ \hat{y}=X\vec{w} y^=Xw。
l ( X , y ⃗ , w ⃗ ) = 1 2 n ∣ ∣ y ⃗ − X w ⃗ ∣ ∣ 2 l(X, \vec{y}, \vec{w}) = \frac{1}{2n}||\vec{y}-X\vec{w}||^2 l(X,y,w)=2n1∣∣y−Xw∣∣2 ∂ ∂ w ⃗ l ( X , y ⃗ , w ⃗ ) = 1 n ( y ⃗ − X w ⃗ ) T X \frac{\partial}{\partial \vec{w}}l(X, \vec{y}, \vec{w}) = \frac{1}{n}(\vec{y}-X\vec{w})^TX ∂w∂l(X,y,w)=n1(y−Xw)TX
损失是凸函数，在梯度等于0时取最优解，所以最优解满足：
∂ ∂ w ⃗ l ( X , y ⃗ , w ⃗ ) = 0 \frac{\partial}{\partial \vec{w}}l(X, \vec{y}, \vec{w})=0 ∂w∂l(X,y,w)=0 ⇔ 1 n ( y ⃗ − X w ⃗ ) T X = 0 \Leftrightarrow \frac{1}{n}(\vec{y}-X\vec{w})^TX=0 ⇔n1(y−Xw)TX=0 ⇔ w ⃗ ∗ = ( X T X ) − 1 X y ⃗ \Leftrightarrow \vec{w}^*=(X^TX)^{-1}X\vec{y} ⇔w∗=(XTX)−1Xy

1.3 总结

• 线性回归是对n维输入的加权，外加偏差。
• 使用平方损失来衡量预测值和真实值的差异。
• 线性回归有显式解。
• 线性回归可以看做是单层神经网络。

二、基础优化算法

2.1 梯度下降

挑选一个初始值 W ⃗ 0 \vec{W}_0 W0，之后不断更新 W ⃗ 0 \vec{W}_0 W0，使其接近最优解。
设置重复迭代参数 t = 1 , 2 , 3 ⋯ t=1, 2, 3 \cdots t=1,2,3⋯
W ⃗ t = W ⃗ t − 1 − η ∂ l ∂ W ⃗ t − 1 \vec{W}_t = \vec{W}_{t-1} - \eta \frac{\partial l}{\partial \vec{W}_{t-1}} Wt=Wt−1−η∂Wt−1∂l

• ∂ l ∂ W ⃗ t − 1 \frac{\partial l}{\partial \vec{W}_{t-1}} ∂Wt−1∂l：损失函数关于 ∂ W ⃗ t − 1 \partial \vec{W}_{t-1} ∂Wt−1的梯度，沿梯度方向将增加损失函数值。
• η \eta η：学习率，即步长的超参数，表示沿着负梯度方向上一次走的距离。
• 通过 ∂ l ∂ W ⃗ t − 1 \frac{\partial l}{\partial \vec{W}_{t-1}} ∂Wt−1∂l和 η \eta η，我们可以沿着梯度下降最快的方向，一步步地得到最小的梯度值。
  

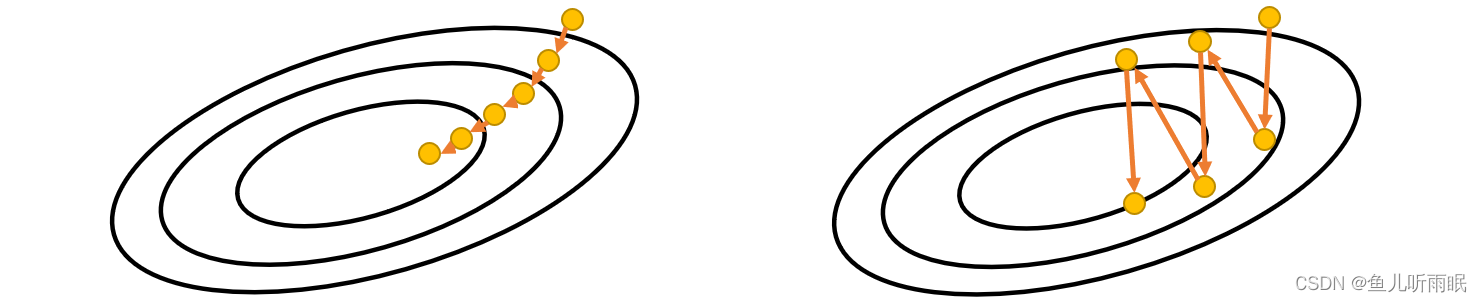
选择学习率不能太大，也不能太小。

• 如果学习率太小，每一次的步长将会很小，梯度下降的速度会大幅下降。
• 如果学习率太大，梯度可能会一直在震荡，并没有真正的下降。
  

2.2 小批量随机梯度下降

在深度学习中，我们很少直接使用梯度下降，通常会采用小批量梯度下降。
这是因为在整个训练集上算梯度的时间成本太高，一个深度神经网络模型可能需要数分钟至数小时。
我们可以随机采样b个样本 i 1 , i 2 , ⋯   , i b i_1, i_2, \cdots, i_b i1,i2,⋯,ib来计算近似损失：
1 b ∑ i ∈ I b l ( x ⃗ i , y i , w ⃗ ) \frac{1}{b} \sum_{i \in I_b}l(\vec{x}_i, y_i, \vec{w}) b1i∈Ib∑l(xi,yi,w)其中，b是批量大小，是深度学习中的另一个重要的超参数。
同样地，批量大小不能太小，也不能太大。

• 如果批量大小太小，每次计算量太小，不适合并行来最大利用计算资源。
• 如果批量大小太大，则内存消耗增加；浪费计算，例如：如果所有样本都是相同的。

2.3 总结

• 梯度下降通过不断沿着反梯度方向更新参数求解。
• 小批量随机梯度下降是深度学习默认的求解算法。
• 两个重要的超参数是批量大小和学习率。

三、线性回归的从零开始实现

我们将从零开始实现整个方法，包括数据流水线、模型、损失函数和小批量随机梯度下降优化器。

3.1 导入的库

本文使用的编辑器为PyCharm，文中代码已针对PyCharm和jupyter的区别进行了修改。下面的代码中，jupyter可以使用%matplotlib inline来内嵌绘图；在PyCharm中使用这句代码则会报错，本文通过plt.show()来展示绘图。

# %matplotlib inline
import torch
import matplotlib.pyplot as plt
import random
from d2l import torch as d2l

3.2 数据集

3.2.1 构造数据集

这里我们采用自己构造的一个简单数据集。根据带有噪声的线性模型构造一个人造数据集。我们使用线性模型参数 w ⃗ = [ 2 − 3.4 ] T \vec{w}=\begin{bmatrix}2 & -3.4\end{bmatrix}^T w=[2−3.4]T、 b = 4.2 b=4.2 b=4.2和噪声项 ε \varepsilon ε生成数据集及其标签：
y ⃗ = X w ⃗ + b + ε \vec{y}=X\vec{w}+b+\varepsilon y=Xw+b+ε

# 生成数据集函数
def synthetic_data(w, b, num_examples):
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))    # 将二维张量转化成一维列向量
# 生成人工数据集
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

3.2.2 展示数据集

features中的每一行都包含一个二维数据样本，labels中的每一行都包含一个一维标签值（一个标量）
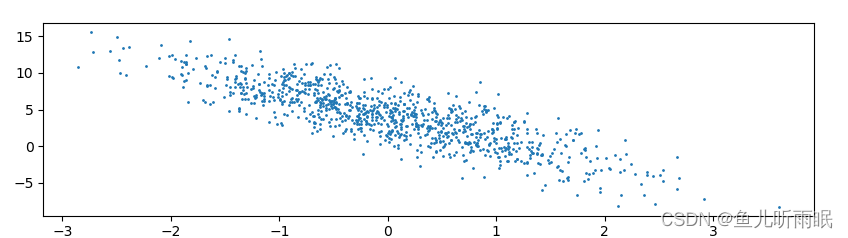
我们可以通过绘图来形象地看到我们的训练样本。

# 展示数据集
print('features: ', features[0], '\nlabels: ', labels[0])
d2l.set_figsize()
d2l.plt.scatter(features[:, (1)].detach().numpy(), labels.detach().numpy(), 1)
plt.show()

3.3 从零开始实现

3.3.1 生成小批量

定义一个data_iter函数，该函数接受批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量。

# 生成小批量函数
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices) # 随机打乱
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(indices[i:min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]
# 生成小批量
batch_size = 10
for x, y in data_iter(batch_size, features, labels):
    print(x, '\n', y)
    break

3.3.2 模型和初始化模型参数

读取了数据集之后，我们要定义初始化模型参数和模型。
我们将权重w随机初始化成均值为0、方差为0.01的正态分布。同时，因为我们要计算梯度，故设置参数requires_grad=True。

# 定义初始化模型参数
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# 定义模型
def linreg(X, w, b):
    """ 线性回归模型 """
    return torch.matmul(X, w) + b

3.3.3 定义损失函数

我们采用均方损失函数。因为y和y_hat可能是行向量或者列向量，所以我们用reshape()方法将它们修改成同样的形状。

# 定义损失函数
def squard_loss(y_hat, y):
    """ 均方损失 """
    return (y_hat - y.reshape(y_hat.shape))**2 / 2

3.3.4 定义优化方法

我们采用SGD优化方法。SGD优化方法的输入需要给定所有的参数（包括w和b）、学习率和批量大小。

# 定义优化方法
def sgd(params, lr, batch_size):
    """ 小批量随机梯度下降 """
    with torch.no_grad():   # 更新的时候，不要进行梯度计算
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

3.3.5 训练过程

# 训练过程
lr = 0.03           # 学习率
num_epochs = 3      # 整个数据扫3遍
net = linreg        # 模型
loss = squard_loss  # 损失函数采用均方损失
for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)   # X和y的小批量损失
        # 因为l的形状是(batch_size, 1)，而不是一个标量。l中所有元素被加到一起。
        # 并以此计算关于(w, b)的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)
    with torch.no_grad():   # 评价进度
        train_1 = loss(net(features, w, b), labels)
        print(f'epoch {
      epoch + 1}, loss {
      float(train_1.mean()):f}')

3.3.6 分析

由于我们使用的是自己构造的数据集，可以看到真实的参数，故我们可以比较真实参数和通过训练学到的参数来评估训练的成功程度。

# 比较真实参数和通过训练学到的参数来评估训练的成功程度
print(f'w的估计误差：{
      true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差：{
      true_b - b}')

四、线性回归的简洁实现

我们可以通过使用深度学习框架来简洁地实现线性回归模型、生成数据集。

4.1 用到的函数

4.2 导入库并生成数据集

import numpy as np
import torch
from torch import nn
from torch.utils import data
from d2l import torch as d2l
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

4.3 读取数据

我们可以调用框架中现有的API来读取数据。

def load_array(data_arrays, batch_size, is_train=True):
    """ 构造一个PyTorch数据迭代器 """
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)
# 调用框架中现有的API来读取数据
batch_size = 10
data_iter = load_array((features, labels), batch_size)
next(iter(data_iter))

4.4 模型的定义

使用框架的预定义好的层，并初始化模型参数。
我们使用nn.Linear()方法来构造一个线性层，并把这个层放到nn.Sequential()容器中。
之后，我们可以通过net[0]来访问到这个层，通过net[0].weight来访问这个层的权重w，因此可以通过net[0].weight.data.normal_(0, 0.01)来将线性层的权重的值替换为正态分布的值。
而net[0].bias则是线性层的偏差，我们通过net[0].bias.data.fill_(0)将这个线性层的偏差设置为0。

# 使用框架的预定义好的层
net = nn.Sequential(nn.Linear(2, 1))
# 初始化模型参数
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

4.5 损失函数

我们的损失函数依然采用均方误差，使用MSELoss类。均方误差也成为平方范数（ L 2 L_2 L2范数）。

loss = nn.MSELoss()

4.6 优化方法

实例化SGD实例。

# SGD
trainer = torch.optim.SGD(net.parameters(), lr=0.03)

4.7 训练过程

# 训练过程
num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X), y)    # 损失函数
        trainer.zero_grad()    # 优化器清零梯度
        l.backward()        # 计算梯度
        trainer.step()      # 模型更新
    l = loss(net(features), labels)
    print(f'epoch {
      epoch + 1}, loss {
      l:f}')

下一篇：【动手学深度学习v2李沐】学习笔记04：Softmax回归、损失函数、图片分类数据集、详细代码实现