Pytorch深度学习(二)-手动实现线性回归
上一讲中我们介绍了梯度下降,下面我们用PyTorch中的Autograd自动求导实现线性回归。
归纳而言,这篇会相对简单,主要包含以下几点:
- PyTorch Autograd 概念介绍
- 利用 Autograd 替代手动求解导数
- 实现 Autograd 方式的线性回归模型
一、PyTorch Autograd 概念介绍
具体查看官网:https://pytorch.org/tutorials/beginner/blitz/autograd_tutorial.html
原理虽然简单,但其中有不少细节需要注意:
首先需要这个函数链是可导的
1.一个 backward 对应一个 grad计算值,所以重复 backward 以及中间环节执行 backward 都会导致 grad 值变化
2.一个 grad 使用完之后,需要记得 设置为 0 ,再次 backward 才能得到正确的值
二、重点代码介绍
1.利用 Autograd 替代手动求解导数
# 设置 requires_grad=True ,告诉PyTorch需要记录params上所有的操作params = torch.tensor([1.0, 0.0], requires_grad=True)# 目前为止 params.grad is None# 执行 backward 后, params.grad 就保存了微分值loss = loss_fn(model(t_u, *params), t_c)loss.backward()# grad 使用完之后,需要记得 设置为 0if params.grad is not None:params.grad.zero_()
2.实现 Autograd 方式的线性回归模型
def training_loop(n_epochs, learning_rate, params, t_u, t_c):for epoch in range(1, n_epochs + 1):if params.grad is not None:params.grad.zero_()t_p = model(t_u, *params)loss = loss_fn(t_p, t_c)loss.backward()params = (params - learning_rate * params.grad).detach().requires_grad_()# print('Epoch %d, Loss %f' % (epoch, float(loss)))# print('Params', params)if epoch % 500 == 0:print('Epoch %d, Loss %f' % (epoch, float(loss)))return params
需要着重解释的是 detach().requires_grad_()
这里的作用就是使 params 脱离之前的函数链,PyTorch重新记录新的函数链
三、完整代码
"""PyTorch 基础入门二: PyTorch 自动求导线性模型实现线性回归参数估计问题: 华氏温度转换"""import torch# 定义输入数据t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]t_c = torch.tensor(t_c)t_u = torch.tensor(t_u)# 对应的线性模型为# t_c = w * t_u + bdef model(t_u, w, b):return w*t_u + b# 定义损失函数# t_p 为模型估计值# t_c 为实验数据def loss_fn(t_p, t_c):squared_diffs = (t_p - t_c)**2return squared_diffs.mean()# 以上跟第一篇保持一致########################################################################## 设置 requires_grad=True ,告诉PyTorch需要记录params上所有的操作params = torch.tensor([1.0, 0.0], requires_grad=True)# 目前为止 params.grad is None# 执行 backward 后, params.grad 就保存了微分值# loss = loss_fn(model(t_u, *params), t_c)# loss.backward()if params.grad is not None:params.grad.zero_()def training_loop(n_epochs, learning_rate, params, t_u, t_c):for epoch in range(1, n_epochs + 1):if params.grad is not None:params.grad.zero_()t_p = model(t_u, *params)loss = loss_fn(t_p, t_c)loss.backward()#params = (params - learning_rate * params.grad).detach().requires_grad_()# print('Epoch %d, Loss %f' % (epoch, float(loss)))# print('Params', params)if epoch % 500 == 0:print('Epoch %d, Loss %f' % (epoch, float(loss)))return params# 特征缩放处理t_un = 0.1 * t_uparams = training_loop(n_epochs = 5000,learning_rate = 1e-2,params = torch.tensor([1.0, 0.0], requires_grad=True),t_u = t_un,t_c = t_c)# 画出图示import matplotlib.pyplot as pltt_p = model(t_un, *params)fig = plt.figure()plt.title(u"PyTorch linear model")plt.xlabel("Fahrenheit")plt.ylabel("Celsius")plt.plot(t_u.numpy(), t_p.detach().numpy())plt.plot(t_u.numpy(), t_c.numpy(), 'o')plt.show()
四、结果展示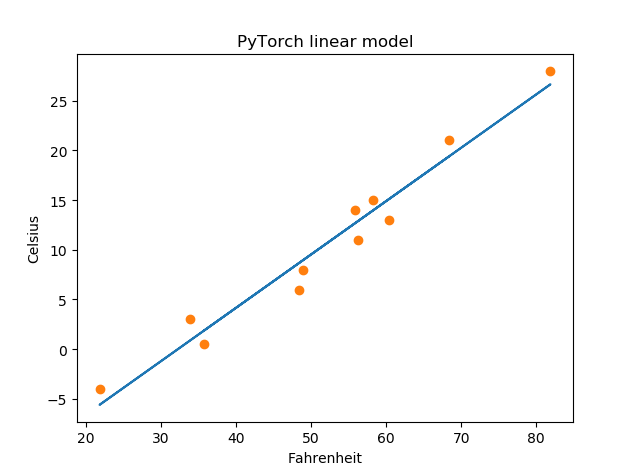



































还没有评论,来说两句吧...