python实现二叉树的遍历-蒲公英云

python实现二叉树的遍历

1 问题

何利用python进行二叉树的遍历。

2 方法**：**

通过创建节点与构建树。
通过借助队列来实现层遍历，再实现后序的遍历

代码清单 1

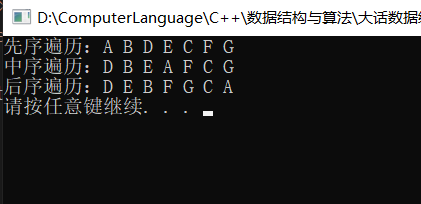
#每个节点有两个后继节点，分别为左子节点和右子节点
class Node():
def init(self, item):
self.elem = item
self.lchild = None
self.rchild = None
#每个树有个根节点
class Tree():
def init(self):
self.root = None
#树具有一个层次结构，从根节点最高层到最低层，每层从左向右遍历。需要借助队列实现
def leveltravel(self):
if self.root == None:
return
queue = [self.root]
while queue:
cur = node = queue.pop(0)
print(cur.elem, end=” “)
if cur.lchild != None:
queue.append(cur.lchild)
if cur.rchild != None:
queue.append(cur.rchild)
#树具有一个层次结构，我们在每层按照从左至右的方向添加节点
def add(self, item):
node = Node(item)
# 如果节点为空
if self.root == None:
self.root = node
return
queue = [self.root]
while queue:
cur = queue.pop(0)
if cur.lchild == None:
cur.lchild = node
return
else:
queue.append(cur.lchild)
if cur.rchild == None:
cur.rchild = node
return
else:
queue.append(cur.rchild)
#先序遍历是先遍历根节点，再遍历左子树，最后遍历右子树。
def preordertravel(self, node):
# 如果节点为空
if node == None:
return
print(node.elem， end=” “)
self.preordertravel(node.lchild)
self.preordertravel(node.rchild)
#中序遍历则先遍历左子树，再遍历根节点，最后遍历右子树。
def inorder_travel(self, node):
# 如果节点为空
if node == None:
return
self.inorder_travel(node.lchild)
print(node.elem, end=” “)
self.inorder_travel(node.rchild)
#后续遍历先遍历左子树，再遍历右子树，最后遍历根节点。
def postorder_travel(self, node):
# 如果节点为空
if node == None:
return
self.postorder_travel(node.lchild)
self.postorder_travel(node.rchild)
print(node.elem, end=” “)
#测试
if __name == “__main“:
t = Tree()
t.add(0)
t.add(1)
t.add(2)
t.add(3)
t.add(4)
t.add(5)
t.add(6)
t.add(7)
t.add(8)
t.add(9)
t.level_travel()
print()
t.preorder_travel(t.root)
print()
t.inorder_travel(t.root)
print()
t.postorder_travel(t.root)
print()

3 结语

在链表中，一个节点只能有一个后继节点和前驱节点。而在树中，一个节点可以有多个后继节点，但只能有一个前驱节点。节点的度表示有几个后继节点，树的度是最大的节点的度。二叉树是度为 2 的树。

在树中，没有前驱节点的节点称为根节点，没有后继节点的节点称为叶子节点。前驱节点也称为父节点，后继节点也称为子节点。具有相同父节点的节点称为兄弟节点。

需要借助队列实现层遍历，而进而的前序中序后序遍历的实现都类似层遍历。