python实现二叉树的遍历

绝地灬酷狼 2022-11-13 09:26 251阅读 0赞

遍历二叉树就是以一定的规则将二叉树中的结点排列成一个线性序列，从而得到二叉树节点的各种遍历序列。其实质就是对一个非线性结构进行线性操作，使在这个序列中，除了第一个和最后一个结点，每个结点都有一个直接前驱和直接后继。
先序遍历
如果二叉树为空，则什么也不做；
否则：
1.访问根节点
2.先序遍历左子树
3.先序遍历右子树

中序遍历
如果二叉树为空，则什么也不做；
否则：
1.中序遍历左子树
2.访问根节点
3.中序遍历右子树
后序遍历
如果二叉树为空，则什么也不做；
否则：
1.后序遍历左子树
2.后序遍历右子树
3.访问根节点

层次遍历：
要进行层次遍历需要借助一个队列。先将二叉树根结点入队，然后出队，访问该结点，如果它有左子树，则将左子树根结点入队；如果它有右子树，则将右子树根结点入队。然后出队，对出队结点访问，如此反复，直到队列为空。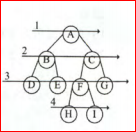
在这里插入图片描述
代码如下：

  1. # 二叉树类
  2. class BTree(object):
  3.     # 初始化
  4.     def __init__(self, data=None, left=None, right=None):
  5.         self.data = data    # 数据域
  6.         self.left = left    # 左子树
  7.         self.right = right  # 右子树
  10.     # 前序遍历:中->左->右
  11.     def preorder(self):
  12.         if self.data:
  13.             print(self.data, end=' ')
  14.         if self.left:
  15.             self.left.preorder()
  16.         if self.right:
  17.             self.right.preorder()
  19.     # 中序遍历：左->中->右
  20.     def inorder(self):
  21.         if self.left :
  22.             self.left.inorder()
  23.         if self.data :
  24.             print(self.data, end=' ')
  25.         if self.right :
  26.             self.right.inorder()
  28.     # 后序遍历：左->右->中
  29.     def postorder(self):
  30.         if self.left :
  31.             self.left.postorder()
  32.         if self.right :
  33.             self.right.postorder()
  34.         if self.data :
  35.             print(self.data, end=' ')
  37.     # 层序遍历：
  38.     def levelorder(self):
  39.         # 返回某个节点的左孩子
  40.         def LChild_Of_Node(node):
  41.             return node.left if node.left  else None
  42.         # 返回某个节点的右孩子
  43.         def RChild_Of_Node(node):
  44.             return node.right if node.right  else None
  46.         # 层序遍历列表
  47.         level_order = []
  48.         # 传入的self为根结点，添加根节点中的数据到level_order,即：二叉树的根节点入队
  49.         if self.data :
  50.             print("self:",self.data)
  51.             level_order.append([self])
  53.         # 二叉树的高度
  54.         height = self.height()
  55.         if height >= 1:
  56.             # 对第二层及其以后的层数进行操作, 在level_order中添加节点而不是数据
  57.             for _ in range(2, height + 1):
  58.                 level = []  # 该层的节点
  59.                 for node in level_order[-1]:
  60.                     # 如果它有左子树，则将左子树节点入队
  61.                     if LChild_Of_Node(node):
  62.                         level.append(LChild_Of_Node(node))
  63.                     # 如果它有右子树，则将右子树结点入队
  64.                     if RChild_Of_Node(node):
  65.                         level.append(RChild_Of_Node(node))
  66.                 if level: # 如果该层非空，则添加该层
  67.                     level_order.append(level)
  69.             # 取出每层中的数据
  70.             for i in range(0, height):  # 层数
  71.                 for index in range(len(level_order[i])):
  72.                     level_order[i][index] = level_order[i][index].data
  73.         return level_order
  76.     # 二叉树的高度
  77.     def height(self):
  78.         # 空的树高度为0, 只有root节点的树高度为1
  79.         if self.data is None:
  80.             return 0
  81.         #左右子树都为空，则当前结点为叶子结点
  82.         elif self.left is None and self.right is None:
  83.             return 1
  84.         elif self.left is None and self.right :
  85.             return 1 + self.right.height()
  86.         elif self.left  and self.right is None:
  87.             return 1 + self.left.height()
  88.         else:
  89.             return 1 + max(self.left.height(), self.right.height())
  91.     # 二叉树的叶子节点
  92.     def leaves(self):
  93.         if self.data is None:
  94.             return None
  95.         elif self.left is None and self.right is None:
  96.             print(self.data, end=' ')
  97.         elif self.left is None and self.right :
  98.             self.right.leaves()
  99.         elif self.right is None and self.left :
  100.             self.left.leaves()
  101.         else:
  102.             self.left.leaves()
  103.             self.right.leaves()
  106. if __name__ == '__main__':
  108.     right_tree = BTree(6)
  109.     right_tree.left = BTree(2)
  110.     right_tree.right = BTree(4)
  112.     left_tree = BTree(5)
  113.     left_tree.left = BTree(1)
  114.     left_tree.right = BTree(3)
  116.     tree = BTree(11)
  117.     tree.left = left_tree
  118.     tree.right = right_tree
  120.     left_tree = BTree(7)
  121.     left_tree.left = BTree(3)
  122.     left_tree.right = BTree(4)
  124.     right_tree = tree # 增加新的变量
  125.     tree = BTree(18)
  126.     tree.left = left_tree
  127.     tree.right = right_tree
  129.     print('先序遍历为:')
  130.     tree.preorder()
  131.     print()
  133.     print('中序遍历为:')
  134.     tree.inorder()
  135.     print()
  137.     print('后序遍历为:')
  138.     tree.postorder()
  139.     print()
  141.     print('层序遍历为:')
  142.     level_order = tree.levelorder()
  143.     print(level_order)
  144.     print()
  146.     height = tree.height()
  147.     print('树的高度为%s.' % height)
  149.     print('叶子节点为：')
  150.     tree.leaves()
  151.     print()
  152. # 先序遍历为:
  153. # 18 7 3 4 11 5 1 3 6 2 4
  154. # 中序遍历为:
  155. # 3 7 4 18 1 5 3 11 2 6 4
  156. # 后序遍历为:
  157. # 3 4 7 1 3 5 2 4 6 11 18
  158. # 层序遍历为:
  159. # self: 18
  160. # [[18], [7, 11], [3, 4, 5, 6], [1, 3, 2, 4]]
  161. #
  162. # 树的高度为4.
  163. # 叶子节点为：
  164. # 3 4 1 3 2 4

也可以换一种方式构造二叉树，利用层序遍历的原理逐层创建，代码如下：

  1. # 二叉树类
  2. class BTree(object):
  3.     # 初始化
  4.     def __init__(self, data=None, left=None, right=None):
  5.         self.data = data    # 数据域
  6.         self.left = left    # 左子树
  7.         self.right = right  # 右子树
  10.     # 前序遍历:中->左->右
  11.     def preorder(self):
  12.         if self.data:
  13.             print(self.data, end=' ')
  14.         if self.left:
  15.             self.left.preorder()
  16.         if self.right:
  17.             self.right.preorder()
  19.     # 中序遍历：左->中->右
  20.     def inorder(self):
  21.         if self.left :
  22.             self.left.inorder()
  23.         if self.data :
  24.             print(self.data, end=' ')
  25.         if self.right :
  26.             self.right.inorder()
  28.     # 后序遍历：左->右->中
  29.     def postorder(self):
  30.         if self.left :
  31.             self.left.postorder()
  32.         if self.right :
  33.             self.right.postorder()
  34.         if self.data :
  35.             print(self.data, end=' ')
  37.     # 层序遍历：
  38.     def levelorder(self):
  39.         # 返回某个节点的左孩子
  40.         def LChild_Of_Node(node):
  41.             return node.left if node.left  else None
  42.         # 返回某个节点的右孩子
  43.         def RChild_Of_Node(node):
  44.             return node.right if node.right  else None
  46.         # 层序遍历列表
  47.         level_order = []
  48.         # 传入的self为根结点，添加根节点中的数据到level_order,即：二叉树的根节点入队
  49.         if self.data :
  50.             print("self:",self.data)
  51.             level_order.append([self])
  53.         # 二叉树的高度
  54.         height = self.height()
  55.         if height >= 1:
  56.             # 对第二层及其以后的层数进行操作, 在level_order中添加节点而不是数据
  57.             for _ in range(2, height + 1):
  58.                 level = []  # 该层的节点
  59.                 for node in level_order[-1]:
  60.                     # 如果它有左子树，则将左子树节点入队
  61.                     if LChild_Of_Node(node):
  62.                         level.append(LChild_Of_Node(node))
  63.                     # 如果它有右子树，则将右子树结点入队
  64.                     if RChild_Of_Node(node):
  65.                         level.append(RChild_Of_Node(node))
  66.                 if level: # 如果该层非空，则添加该层
  67.                     level_order.append(level)
  69.             # 取出每层中的数据
  70.             for i in range(0, height):  # 层数
  71.                 for index in range(len(level_order[i])):
  72.                     level_order[i][index] = level_order[i][index].data
  73.         return level_order
  76.     # 二叉树的高度
  77.     def height(self):
  78.         # 空的树高度为0, 只有root节点的树高度为1
  79.         if self.data is None:
  80.             return 0
  81.         #左右子树都为空，则当前结点为叶子结点
  82.         elif self.left is None and self.right is None:
  83.             return 1
  84.         elif self.left is None and self.right :
  85.             return 1 + self.right.height()
  86.         elif self.left  and self.right is None:
  87.             return 1 + self.left.height()
  88.         else:
  89.             return 1 + max(self.left.height(), self.right.height())
  91.     # 二叉树的叶子节点
  92.     def leaves(self):
  93.         if self.data is None:
  94.             return None
  95.         elif self.left is None and self.right is None:
  96.             print(self.data, end=' ')
  97.         elif self.left is None and self.right :
  98.             self.right.leaves()
  99.         elif self.right is None and self.left :
  100.             self.left.leaves()
  101.         else:
  102.             self.left.leaves()
  103.             self.right.leaves()
  111. # 利用列表构造二叉树
  112. # 列表中至少有一个元素
  113. def create_BTree_By_List(array):
  115.     i = 1
  116.     # 将原数组拆成层次遍历的数组，每一项都储存这一层所有的节点的数据
  117.     level_order = []
  118.     sum = 1
  119.     #二叉树每层元素数目为pow(2,n-1),索引为i-1:i*2-1
  120.     while sum < len(array):
  121.         level_order.append(array[i-1:2*i-1])
  122.         i *= 2
  123.         sum += i
  124.     level_order.append(array[i-1:])#如果不是满二叉树，则剩余的放到最后一层
  126.     # BTree_list: 这一层所有的节点组成的列表
  127.     # forword_level: 上一层节点的数据组成的列表
  128.     def Create_BTree_One_Step_Up(BTree_list, forword_level):
  129.         new_BTree_list = []#最终得到一层有左右子树的结点
  130.         i = 0
  131.         for elem in forword_level:#这是父节点的集合，给结点分配左右子树
  132.             root = BTree(elem)
  133.             if 2*i < len(BTree_list):#左子树
  134.                 root.left = BTree_list[2*i]
  135.             if 2*i+1 < len(BTree_list):#右子树
  136.                 root.right = BTree_list[2*i+1]
  137.             new_BTree_list.append(root)
  138.             i += 1
  139.         return new_BTree_list
  141.     # 只有一层：即只有一个节点
  142.     if len(level_order) == 1:
  143.         return BTree(level_order[0][0])
  144.     else: # 二叉树的层数大于1
  145.         # 创建最后一层的节点列表
  146.         BTree_list = [BTree(elem) for elem in level_order[-1]]
  147.         # 从下往上，逐层创建二叉树:BTree_list是每一层的节点集合
  148.         for i in range(len(level_order)-2, -1, -1):
  149.             BTree_list = Create_BTree_One_Step_Up(BTree_list, level_order[i])
  150.         return BTree_list[0]
  154. if __name__ == '__main__':
  156.     array = [chr(x) for x in range(65,91)]
  157.     tree = create_BTree_By_List(array)
  159.     print('先序遍历为:')
  160.     tree.preorder()
  161.     height = tree.height()
  162.     print('树的高度为%s.'%height)
  163.     print('层序遍历为:')
  164.     level_order = tree.levelorder()
  165.     print(level_order)
  166.     print('叶子节点为：')
  167.     tree.leaves()
  169. # 先序遍历为:
  170. # A B D H P Q I R S E J T U K V W C F L X Y M Z G N O 树的高度为5.
  171. # 层序遍历为:
  172. # self: A
  173. # [['A'], ['B', 'C'], ['D', 'E', 'F', 'G'], ['H', 'I', 'J', 'K', 'L', 'M', 'N', 'O'], ['P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']]
  174. # 叶子节点为：
  175. # P Q R S T U V W X Y Z N O

发表评论

表情：
评论列表 （有 0 条评论，251人围观）

还没有评论，来说两句吧...

相关阅读

    相关 python实现二叉树的遍历

    遍历二叉树就是以一定的规则将二叉树中的结点排列成一个线性序列，从而得到二叉树节点的各种遍历序列。其实质就是对一个非线性结构进行线性操作，使在这个序列中，除了第一个和最后一个结点

    绝地灬酷狼绝地灬酷狼/ 0 赞/ 252 阅读

    相关 二叉树遍历c++实现

    //自己还真是个菜鸡，大一学了一年c++，现在还在基础的语法上转圈，还没有意识到c++真正的 //的强大之处在于它的多变，封装，等算法告一段落了在考虑是往Jav

    谁践踏了优雅谁践踏了优雅/ 0 赞/ 261 阅读

    相关 二叉树的遍历 python

    从二叉树的根节点出发，节点的遍历分为三个主要步骤：对当前节点进行操作（称为“访问”节点，或者根节点）、遍历左边子节点、遍历右边子节点。访问节点顺序的不同也就形成了不同的遍历方式

    红太狼红太狼/ 0 赞/ 226 阅读