动态规划算法-蒲公英云

动态规划算法

动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解，创立了解决这类过程优化问题的新方法——动态规划。

动态规划的基本思想
将原问题划分为子问题，以自底向上的方式求解问题对所有已经求解的子问题，动态规划法将子问题的解记录到表格中，求解较大的子问题时，一旦要用到已求解的较小子问题的解，就返回表格中已常数时间查询较小子问题的解并直接使用。
动态规划法的基本要素
最优子结构性质与子问题重叠性质。
动态规划法的基本步骤
1）分析问题的最优解性质，刻画最优解的结构特征。
2）建立最优值的递归定义。
3）以自底向上的方式计算出最优值。
4）构造问题的最优解。
分类与举例
动态规划一般可分为线性动规，区域动规，树形动规，背包动规四类。
举例：
线性动规：拦截导弹，合唱队形，挖地雷，建学校，剑客决斗等；
区域动规：石子合并，加分二叉树，统计单词个数，炮兵布阵等；
树形动规：贪吃的九头龙，二分查找树，聚会的欢乐，数字三角形等；
背包问题：01背包问题，完全背包问题，分组背包问题，二维背包，装箱问题，挤牛奶（同济ACM第1132题）等；
应用实例：
最短路径问题，项目管理，网络流优化等；
举例：最长公共子序列
递归定义最优解：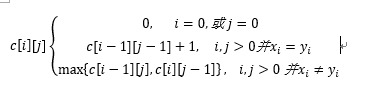

代码实现：

public static int lcsLength(char[] x,char[] y,int[][] b) {
        //构造矩阵大小
        int m = x.length+1;
        int n = y.length+1;
        int[][] c = new int[m][n];
        //初始化边界
        for(int i=0;i<m;i++)
            c[i][0] = 0;
        for(int i=0;i<n;i++)
            c[0][i] = 0;
        for(int i=1;i<m;i++) {
            for(int j=1;j<n;j++) {
                if(x[i-1] == y[j-1]) {
                    c[i][j] = c[i-1][j-1] + 1;
                    b[i][j] = 1;
                }
                else {
                    if(c[i-1][j] > c[i][j-1]) {
                        c[i][j] = c[i-1][j];
                        b[i][j] = 2;
                    }
                    else {
                        c[i][j] = c[i][j-1];
                        b[i][j] = 3;
                    }
                }
            }
        }
        return c[m-1][n-1];
    }
    public static void lcs(int i,int j,char[] x,int[][] b) {
        if(i==0||j==0)
            return;
        if(b[i][j] == 1) {
            lcs(i-1,j-1,x,b);
            System.out.println(x[i-1]);
        }
        else if(b[i][j] == 2)
            lcs(i-1,j,x,b);
        else
            lcs(i,j-1,x,b);
    }