常用数据结构之Heap(堆)

- 日理万妓 2022-12-10 05:58 158阅读 0赞

# 1.简介 #

接着上一篇 [数组和链表][Link 1]，我们今天来聊一聊堆。我们都知道在操作系统中有堆栈这一概念，学过java的同学都知道java虚拟机中也有堆栈这么一说。栈负责管理函数的上下文以及一些基本类型变量，这一块由系统管理。堆存放新建的对象，并且会将其地址指向栈中的一个引用变量。如果没有任何引用，对象就成为垃圾对象，最后由垃圾回收器回收。但是我这里要聊的并不是内存中的堆，内存一般使用链表的形式来管理。但数据结构中堆的概念，相当于一种优先队列。

# 2.堆的定义和性质 #

## 1.定义 ##

堆就是一棵**完全二叉树**，所谓的完全二叉树指的是树中的每一个节点位置和**满二叉树**中的位置相同，所谓的满二叉树指的是每一层树的节点都达到最大值(也就是树的每一层都被填满了)；

**最大堆**：一个堆中父节点的值总是比子节点要大(优先队列)

**最小堆**：父节点的值总是比子节点要小

![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2dhb2JpbmcxOTkz_size_16_color_FFFFFF_t_70][]

## 2.性质一节点位置关系 ##

1.已知父节点位置是i,其左子节点的位置是 2i+1,右子节点的位置是2i+2

2.已知子节点的位置是i,其父节点的位置是 (i-1)/2

## 3.性质二高度 ##

堆的高度是根节点到最远叶节点所需要走的步数，等于堆的层数减一。假设一共有n个节点，那么这n个节点组成的堆的高度为![floor(logn)][floor_logn],此处对数以二为底。

如果堆的最下面一层被填满，则最小面一层的节点数量为![2^\{h\}][2_h],前面所有层的节点总和为![2^\{h\}-1][2_h_-1],那么这个堆这种全部的节点数为![2^\{h+1\}-1][2_h_1_-1]

## 4.堆构建的过程 ##

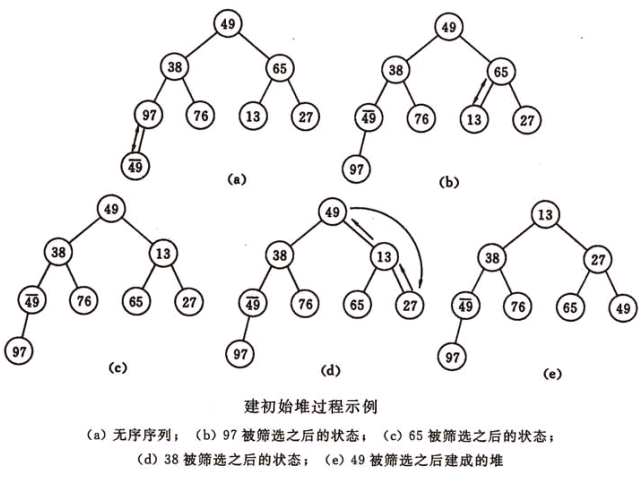
如图所示我们构建一个最小堆，实现的过程就是将每一个元素插入到堆的最后一位，然后不断的向上执行 堆化操作。下面的代码实现会更清晰的体现出来这一点。

![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2dhb2JpbmcxOTkz_size_16_color_FFFFFF_t_70 1][]

# 3.基本功能代码实现 #

基本的功能包括三点：

1.添加新元素到堆中，先将元素插入到最后一位，再不断和父节点比较，直到位置不再变换

2.弹出堆顶元素，弹出后将最后一位放入第一位，不断和子节点进行比较，直到位置不再变换。

3.优先队列：将一个数组变成堆，其实就是将每一个元素插入到一个空堆里面，按照优先级排序。

#-*- coding:utf-8 -*-
    #实现一个最大堆
    #1.使用数组来存放元素
    #2.两个核心 方法 shift_up(将元素和父节点比较，如果顺序不对就更换位置) 
    #shift_down (将元素和子节点比较，如果顺序不对就更换位置)
    #3.添加元素 加入到最后面  然后进行 shift_up(-1)进行堆顺序调整
    #4.取出元素 弹出第一个  将最后一个放在第一的位置  然后shift_down(0)进行堆顺序调整
    class MaxHeap(object):
        #双下划线表示私有 外部不可以访问 子类也不可以
        # 单下划线表示半私有 外部可以访问 子类可以访问
        def __init__(self):
            self.array=[] #用数组来存放元素
        def _parent(self,index):
            return int((index-1)/2)
        def _leftchild(self,index):
            return int(index*2+1)
        def _rightchild(self,index):
            return int(index*2+2)
        def get_size(self):
            return len(self.array)
        # 将每一个元素和父节点进行比较，如果大于父节点的值则进行位置交换
        def shift_up(self,K):
            parent = self._parent(K)
            if K>0 and self.array[K]>self.array[parent]:
                self.array[K],self.array[parent]=self.array[parent],self.array[K]
                self.shift_up(parent)
        #将节点和自己的子节点比较，如果子节点大于父节点则调换位置
        def shift_down(self,K):
            left_child = self._leftchild(K)
            right_child = self._rightchild(K)
            array_size = self.get_size()
            max_position = K
            if left_child+1<array_size and self.array[max_position] < self.array[left_child]:
                max_position = left_child
            if right_child+1 < array_size and self.array[max_position] < self.array[right_child]:
                max_position = right_child
            if max_position != K:
                self.array[max_position], self.array[K] = self.array[K], self.array[max_position]
                self.shift_down(max_position)
        #将一个元素插入堆,添加到最后一位，然后执行shift_up
        def push(self,V):
            self.array.append(V)
            self.shift_up(len(self.array)-1)
        #删除元素，顶部弹出，将最后一个元素放入顶部，执行shift_down
        def pop(self):
            max_value = self.array[0]
            self.array[0],self.array[len(self.array)-1] = self.array[len(self.array)-1],self.array[0]
            self.array.pop(-1)
            self.shift_down(0)
            return max_value
        #查看堆顶元素
        def find_max(self):
            return self.array[0]
        #将一个数组进行堆化,就是将元素一个个插入堆中
        def heapify(self,arr):
            for i in arr:
                self.push(i)
            return self.array
        #遍历堆
        def listHeap(self):
            return self.array
    array = [1,2,3,4,17,6,7,8,9,10]
    maxHeap = MaxHeap()
    print(maxHeap.heapify(array))
    print(maxHeap.pop())
    maxHeap.push(15)
    print(maxHeap.listHeap())

# 4.堆的应用 #

## 1.堆排序 ##

堆排序的思想就是，先将一组数据进行堆化，然后再一个个的弹出堆顶的元素。整体的复杂度为O(nlogn)!

def heap_sort(self,data):
            self.heapify(data)
            heap_sort = []
            for i in self.array:
                heap_sort.append(i)
            return heap_sort

## 2.获取前K个最大的数 ##

其实和上面堆排序的思想一致，只不过我们并不需要将是所有元素进行排序。只是将元素堆化以后，再进行K次堆顶弹出就是

def get_max_k(self,data,K):
            self.heapify(data)
            max_k = []
            for i in range(K):
                max_k.append(self.pop())
            return max_k

# 5.总结 #

本文介绍了数据结构中堆的概念，其并不是操作系统中内存管理的堆的概念。我们知道堆是一棵完全二叉树，对于最大堆来说，每一个节点的值大于其子节点的值(最小堆相反)，这样就保证了堆顶的元素是最大的。对于堆，我们一般有存和取两种操作 ，存的时候将新值插入到最后一位，然后不断向上进行堆化。取的时候弹出堆顶的元素，并且将最后一位元素放入堆顶，不断向下进行堆化操作。

我们注意到堆中的数据并不是有序的，其仅仅符合父节点大于子节点，可以被利用的只有堆顶的元素。可以说是一种比较粗糙的序列。但就是因为其要求不多，可以让我们很简单的插入删除元素。并且因为其堆顶元素总是最大的，可以让我们很简单的实现堆排序，优先队列，前K个最大数等复杂功能。可以说它的限制，同时也就是它的优势。

# 6.闲言碎语 #

人们说：“你是一个好人，他是一头好猪。”在人的眼中看来，那些肉质鲜美，体型庞大的猪就是好猪。在猪看来，那些人都吃饱了还要去上班，简直就是一群大笨蛋，一群从骨髓深处被奴役的生物。人类的语言有一点太复杂了，那么枯燥的英文单词背的我痛不欲生。从本质上讲语言的复杂程度是和谎言的数量成正比的，如果只是为了表达喜欢，甚至连语言都不需要，抱一下亲一下，或者一个眼神对方就足以明白。可是如果不喜欢却要表达喜欢的话，就只能通过语言了。对于猪来说，就简单的多了。他们的世界里面只有‘哼’、‘哼哼’和‘哼哼哼’！这才是最高级的语言，最有效的表达方式。喜欢就是哼，不喜欢就是哼哼，好吃就是哼，不好吃就是哼哼哼。从深度学习自然语言的角度来讲，人类的语言就是最原始的one-hot编码，简陋而朴素。你再看看猪的语言，多么高级的抽象，多么完美的封装，绝对的高内聚，完全的松耦合！再说说好人好猪和语言之间的关系，人们的语言是阻止人们认识真理最好的方式，因为那是一种装饰和伪装，而真理是绝对真实的。即使很多时候，我们觉得自己是怎么想的就是怎么说的，但其实也只是从语言中找到了一些离思想比较近的表达而已。语言符号已经成为了我们主要的思考方式，仔细回想，语言和逻辑就是就是我们思想行走的方式。你进到了一片梅子林，是绝对摘不到苹果的，同样语言之中没有真理。再看看猪吧，从来没有哪一个猪被判为强奸犯，也从来没有哪一个猪被同伴拉出去枪毙。也就是说在它们的社会定义中，没有坏这一个概念。这也验证了一句名言，人人皆为尧舜。所以说根本就没有一个好人，相反，根本就没有一头坏猪！

对不起，伟大的人类语言！我之所以这么消极，是因为我快被英文单词逼疯了。

超帅小姐姐

[Link 1]: https://blog.csdn.net/gaobing1993/article/details/108666410
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2dhb2JpbmcxOTkz_size_16_color_FFFFFF_t_70]: /images/20221123/a1731700bfba4392a78bbe88e3af810a.png
[floor_logn]: https://private.codecogs.com/gif.latex?floor%28logn%29
[2_h]: https://private.codecogs.com/gif.latex?2%5E%7Bh%7D
[2_h_-1]: https://private.codecogs.com/gif.latex?2%5E%7Bh%7D-1
[2_h_1_-1]: https://private.codecogs.com/gif.latex?2%5E%7Bh&plus;1%7D-1
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2dhb2JpbmcxOTkz_size_16_color_FFFFFF_t_70 1]: /images/20221123/71c42ff8f361449993a3b57305994f7a.png