回溯法-N皇后问题
一、N皇后问题
n皇后问题：要求在一个n×n的棋盘上放置n个皇后，使得任意两个皇后不在同一行或同一列或同一斜线上。
二、回溯法
回溯法是一类非常重要的算法设计方法，有“通用解题法”之称。
回溯法（探索与回溯法）：一种选优搜索法，又称试探法。利用试探性的方法，在包含问题所有解的解空间树中，将可能的结果搜索一遍，从而获得满足条件的解。搜索过程采用深度遍历策略，并随时判定结点是否满足条件要求，满足要求就继续向下搜索，若不满足要求则回溯到上一层，这种解决问题的方法称为回溯法。
回溯法解求解问题步骤
- 针对给定问题，定义问题的解空间树
- 确定易于搜索的解空间结构
- 以深度优先方式搜索解空间，并且在搜索过程中永剪枝函数避免无效搜索。
下面给出一个三皇后问题的解空间树（3皇后问题无解），树中第i层的结点决定第i行皇后的摆放位置，均有三种不同的选择，便形成了三个孩子结点，但其中不包括不符合要求的布局。N皇后问题解空间树与三皇后问题解空间树类似。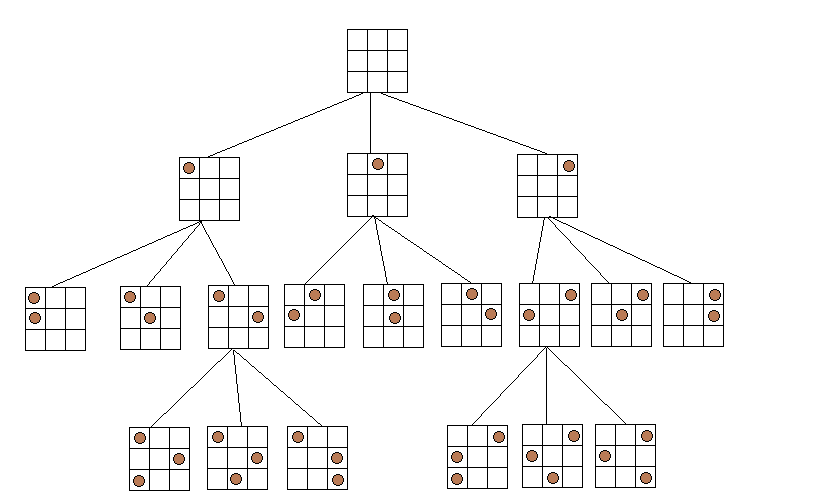
N皇后Java程序算法
public class nQueen {private static int n = 4;private static int count = 0;//排法结果private static int[] arrResult = new int[n];public static void main(String[] args) {//从第一行开始向下查找search(0);System.out.println("结果数量：" + count);}//第i行，总的n行n列public static void search(int i) {if (i >= n) {//一组查找结束count++;System.out.println("结果"+Arrays.toString(arrResult));} else {//遍历所有列for (int j = 0; j < n; j++) {//将该列放置queenarrResult[i] = j;//如果将行的每一列都找不到存放点，则进行回朔查找。if (isCanPlace(arrResult, i, j)) {//可存放，继续下一行search(i + 1);}}}}//是否可放置，false为不可放置，true为可放置public static boolean isCanPlace(int arr[], int i, int j) {//遍历所有行数for (int k = 0; k < i; k++) {//行存在if (arr[k] == arr[i]) {return false;}//对角线存在if ((Math.abs(k - i)) == Math.abs(arr[k] - arr[i])) {return false;}}return true;}}
解析：
结果集arrResult[4]=[0,0,0,0]arr[] 第i行 0 1 2 2(第二次) 3列0 arrResult[]=[0,0,0,0] arrResult[]=[0,0,0,0] 不满足，继续下一列 arrResult[]=[0,2,0,0] 不满足，继续下一列 arrResult[]=[0,3,0,0] 不满足，继续下一列列1 可以放置，进入下一行 arrResult[]=[0,1,0,0] 不满足，继续下一列 arrResult[]=[0,2,1,0] 不满足，继续下一列 arrResult[]=[0,3,1,0] 满足列2 arrResult[]=[0,2,0,0] 满足，下一行 arrResult[]=[0,2,2,0] 不满足，继续下一列列3 arrResult[]=[0,3,3,0] =>返回到这行,满足 arrResult[]=[0,2,3,0] 不满足，返回上一行进行查找
结果：
结果[1, 3, 0, 2]结果[2, 0, 3, 1]结果数量：2
骑猪看日落
秒速五厘米
小鱼儿
灰太狼
小灰灰
╰+哭是因爲堅強的太久メ
还没有评论，来说两句吧...