回溯法——八 / N 皇后问题-蒲公英云

回溯法的基本做法是搜索，或是一种组织得井井有条的，能避免不必要搜索的穷举式搜索法。这种方法适用于解一些组合数相当大的问题。

回溯法在问题的解空间树中，按深度优先策略，从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时，先判断该结点是否包含问题的解。如果肯定不包含，则跳过对该结点为根的子树的搜索，逐层向其祖先结点回溯；否则，进入该子树，继续按深度优先策略搜索。

回溯法指导思想——走不通，就掉头。设计过程：确定问题的解空间；确定结点的扩展规则；搜索。

n皇后问题

要在n*n的国际象棋棋盘中放n个皇后，使任意两个皇后都不能互相吃掉。规则：皇后能吃掉同一行、同一列、同一对角线的任意棋子。求所有的解。n=8是就是著名的八皇后问题了。

设八个皇后为xi，分别在第i行(i=1，2，3，4……，8)；

问题的解状态：可以用(1,x1)，(2,x2)，……，(8,x8)表示8个皇后的位置；

由于行号固定，可简单记为：(x1,x2,x3,x4,x5,x6,x7,x8)；

问题的解空间：(x1,x2,x3,x4,x5,x6,x7,x8)，1≤xi≤8(i=1，2，3，4……，8)，共88个状态；

约束条件：八个(1,x1),(2,x2) ,(3,x3),(4,x4) ,(5,x5), (6,x6) , (7,x7), (8,x8)不在同一行、同一列和同一对角线上。

盲目的枚举算法：通过8重循环模拟搜索空间中的88个状态，从中找出满足约束条件的“答案状态”。程序如下：

/*
 *说明：八皇后——盲目迭代法
 *日期：2013-12-18
 */
#include <iostream>
using namespace std;
bool check_1(int a[],int n)
{
for(int i=2;i<=n;i++)
{
    for(int j=1;j<=i-1;j++)
    {
        if ((a[i]==a[j])||(abs(a[i]-a[j])==i-j))
        {
            return false;
        }
    }
}
return true;//不冲突
}
void queens_1()
{
    int a[9];
    int count = 0;
    for(a[1]=1;a[1]<=8;a[1]++)
    {
        for(a[2]=1;a[2]<=8;a[2]++)
        {
            for(a[3]=1;a[3]<=8;a[3]++)
            {
                for(a[4]=1;a[4]<=8;a[4]++)
                {
                    for(a[5]=1;a[5]<=8;a[5]++)
                    {
                        for(a[6]=1;a[6]<=8;a[6]++)
                        {
                            for(a[7]=1;a[7]<=8;a[7]++)
                            {
                                for(a[8]=1;a[8]<=8;a[8]++)
                                {
                                    if(!check_1(a,8))   
                                        continue;
                                    else
                                    {
                                        for(int i=1;i<=8;i++)  
                                        {
                                            cout<<a[i];
                                        }
                                        cout<<endl;
                                        count++;
                                    }
                                }
                            }
                        }
                    }
                }
            }
        }
    }
    cout<<count<<endl;
}
void main()
{
    queens_1();
}

程序思想比较简单，最后可知共92种摆放方法。如果能够排除那些没有前途的状态，会节约时间——回溯法（走不通，就回头）。

bool check_2 (int a[ ],int n)
{//多次被调用，只需一重循环 
    for(int i=1;i<=n-1;i++)
    {
        if((abs(a[i]-a[n])==n-i)||(a[i]==a[n]))
            return false;
    }      
    return true;
}
void queens_2()
{
    int a[9];
    int count = 0;
    for(a[1]=1;a[1]<=8;a[1]++)
    {
        for(a[2]=1;a[2]<=8;a[2]++)
        {
            if (!check_2(a,2))  continue;
            for(a[3]=1;a[3]<=8;a[3]++)
            {
                if (!check_2(a,3))  continue;
                for(a[4]=1;a[4]<=8;a[4]++)
                {
                    if (!check_2(a,4))  continue;
                    for(a[5]=1;a[5]<=8;a[5]++)
                    {
                        if (!check_2(a,5))  continue;
                        for(a[6]=1;a[6]<=8;a[6]++)
                        {
                            if (!check_2(a,6))  continue;
                            for(a[7]=1;a[7]<=8;a[7]++)
                            {
                                if (!check_2(a,7))  continue;
                                for(a[8]=1;a[8]<=8;a[8]++)
                                {
                                    if (!check_2(a,8))  
                                        continue;
                                    else
                                    {
                                        for(int i=1;i<=8;i++)  
                                        {
                                            cout<<a[i];
                                        }
                                        cout<<endl;
                                        count++;
                                    }
                                }
                            }
                        }
                    }
                }
            }
        }
    }
    cout<<count<<endl;
}
void main()
{
    queens_2();
}

n此算法可读性很好，体现了“回溯”。但它只针对八皇后问题，解决任意的n皇后问题还要修改程序结构。如果要解决n皇后的问题，就需要将n作为参数传递给函数，函数需要重写来实现回溯（不能采用级联的for循环，n不确定）；从另一方面，程序中出现了大量的for循环，而且for中的函数结构很相似，自然想到的是递归迭代回溯。这就是回溯比较常用的两种实现方法：非递归回溯和递归回溯。

非递归回溯的程序实现：

void backdate (int n)
{  
    int count = 0;
    int a[100];
    int k = 1;
    a[1]=0;   
    while(k>0)
    {
        a[k]=a[k]+1;//对应for循环的1~n
        while((a[k]<=n)&&(!check_2(a,k)))//搜索第k个皇后位置
        {
            a[k]=a[k]+1;
        }
        if(a[k]<=n)//找到了合理的位置
        {
            if(k==n )
            {//找到一组解
                for(int i=1;i<=8;i++)  
                {
                    cout<<a[i];
                }
                cout<<endl;
                count++;
            } 
            else 
            {
                k=k+1;//继续为第k+1个皇后找到位置，对应下一级for循环 
                a[k]=0;//下一个皇后一定要从头开始搜索
            }
        }
        else
        {
            k=k-1;//回溯,对应执行外内层for循环回到更上层 
        }
    }
    cout<<count<<endl;
}
void main()
{
    backdate(8);
}

这样也可以得到，8皇后问题的92中结果。更简单、可读的方法是采用递归的方式，如下：

int a[100], n, count;
void backtrack(int k)
{
    if (k>n)//找到解
    {
        for(int i=1;i<=8;i++)  
        {
            cout<<a[i];
        }
        cout<<endl;
        count++;
    }
    else
    {
        for (int i = 1;i <=n; i++)
        {
            a[k] = i;
            if (check_2(a,k) == 1)
            {backtrack(k+1);}
        }
    }
}
void main()
{
    n=8,count=0;
    backtrack(1);
    cout<<count<<endl;
}

可见，递归调用大大减少了代码量，也增加了程序的可读性。给出其中的一个解，如下：

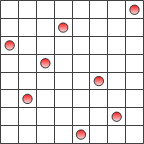
将这个八皇后扩展到n皇后问题。下面是java版的代码：

public class N_Queens {
    static int n=8 ;
    static long sum ;
    static int[] x ;
    public static void main(String[] args) {
        sum =0;
        x=new int[n+1];
        for (int i = 0; i <=n  ; i++) {
             x[i]=0;
        }
        Backtrack(1);
        System.out.println(sum);
    }
    static void Backtrack(int index){
        if(index>n){
          sum++;
        }else{
        for(int i=1;i<=n;i++){
            x[index]=i;
            if(Containt(index)){
                Backtrack(index+1);
            }
        }
        }
    }
    //约束函数
    //保证不在同一列上，而且不在统一斜线上， 为什么不去保证不在同一行上，因为默认数组的索引就不是相同的
    private static boolean Containt(int k) {//t代表试探皇后的位置
        for (int j = 1; j <k ; j++) {//在保证当前皇后位置在[1,t)之间不存在满足同一斜线或者同一列的要求
            if((Math.abs(k-j)==Math.abs(x[j]-x[k]))||(x[j]==x[k])){
                  return false;
            }
        }
        return true;
    }
}