排序 - 计数排序（6）-蒲公英云

排序 - 计数排序（6）

你的名字 2022-10-02 14:50 176阅读 0赞

概念

计数排序是一个非基于比较的排序算法。

当输入的元素是 n 个 0 到 k 之间的整数时，它的运行时间是 Ο(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存，当然这是一种牺牲空间换取时间的做法，而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序（基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序，堆排序）。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。

例如：计数排序是用来排序0到100之间的数字的最好的算法，但是它不适合按字母顺序排序人名。但是，计数排序可以用在基数排序中的算法来排序数据范围很大的数组。

通俗地理解，例如有 10 个年龄不同的人，统计出有 8 个人的年龄比 A 小，那 A 的年龄就排在第 9 位,用这个方法可以得到其他每个人的位置,也就排好了序。当然，年龄有重复时需要特殊处理（保证稳定性），这就是为什么最后要反向填充目标数组，以及将每个数字的统计减去 1 的原因。

实现原理

算法的步骤如下：

（1）找出待排序的数组中最大和最小的元素
（2）统计数组中每个值为i的元素出现的次数，存入数组C的第i项
（3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
（4）反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

排序演示

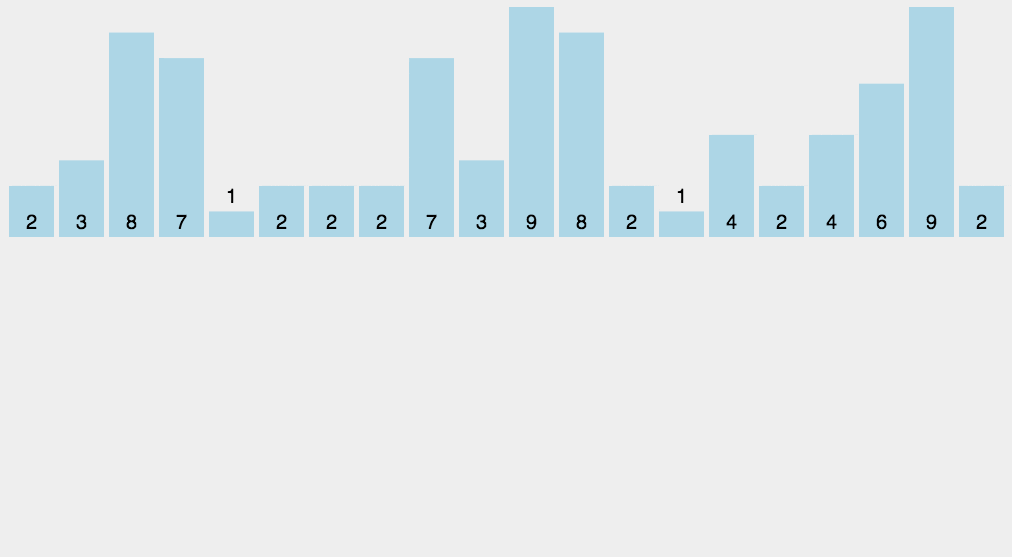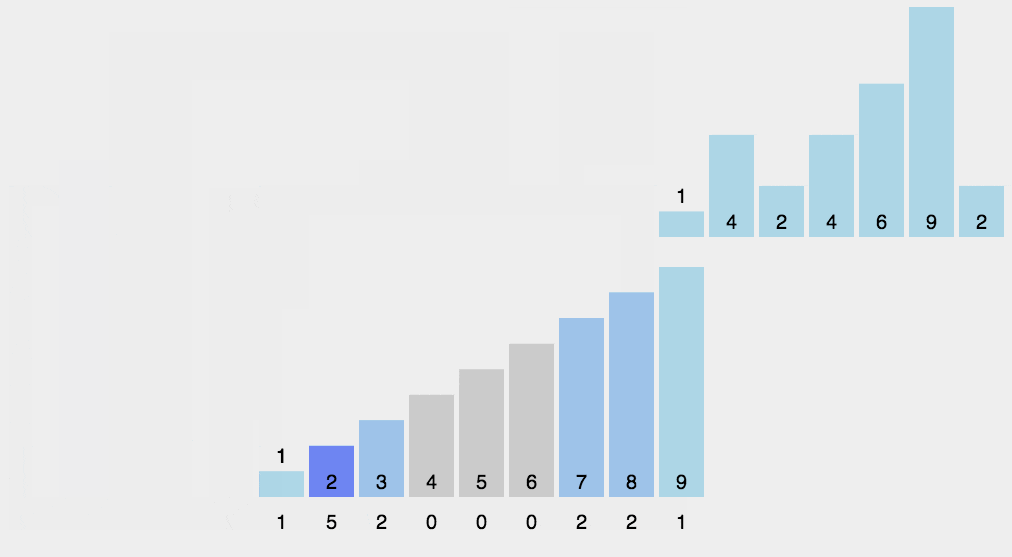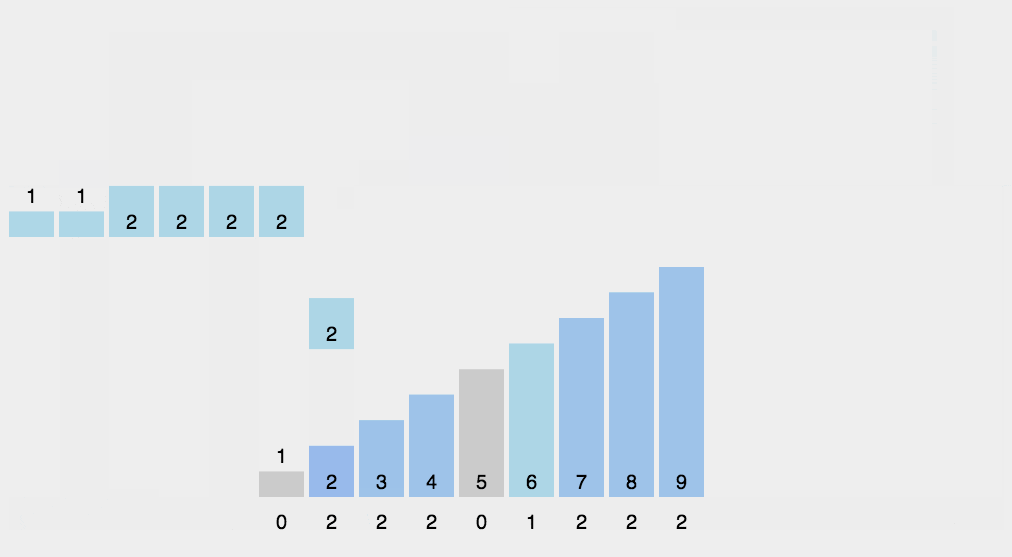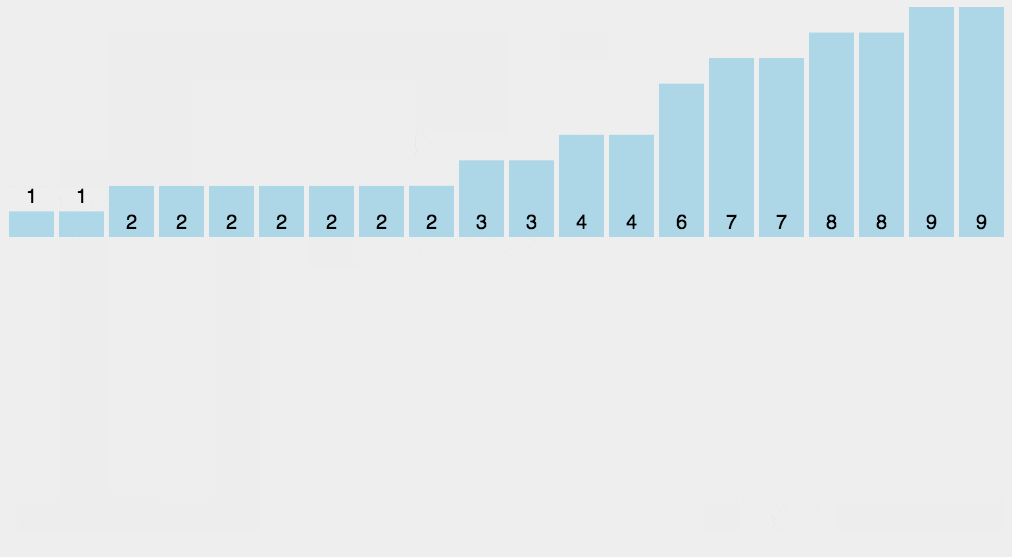
实现代码

public static int[] countSort(int[] a){
        int b[] = new int[a.length];
        int max = a[0],min = a[0];
        //第一步：找出待排序的数组中最大和最小的元素，并算出差值k
        for(int i:a){
            if(i>max){
                max=i;
            }
            if(i<min){
                min=i;
            }
        }
        //这里k的大小是要排序的数组中，元素大小的极值差+1
        int k=max-min+1;
        int c[]=new int[k];
        //第二步：统计数组中每个值为i的元素出现的次数，存入数组C的第i项
        for(int i=0;i<a.length;++i){
            c[a[i]-min]+=1;//优化过的地方，减小了数组c的大小
        }
        //第三步：对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
        for(int i=1;i<c.length;++i){
            c[i]=c[i]+c[i-1];
        }
        //第四步：反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1
        for(int i=a.length-1;i>=0;--i){
            b[--c[a[i]-min]]=a[i];//按存取的方式取出c的元素
        }
        return b; 
}

算法分析

时间复杂度
代码第1,2,4步都涉及到遍历原始数列，运算量都是N，第3步遍历统计数列，运算量是k，所以总体运算量是3N+k，去掉系数，时间复杂度为Ο(n+k)（其中k是整数的范围）
空间复杂度
如果不考虑结果数组，只考虑统计数组大小的话，空间复杂度是O（k）；如果考虑结果数组，则需要 O(n+k) 额外空间
算法稳定性
计数排序是稳定的。

使用场景

当数列最大值最小值的差距过大时，不适合计数排序。
比如给定10个随机整数，范围在0到1亿之间，这时候使用计数排序，需要创建1亿的数组。不但严重浪费空间，而且时间复杂度也随之升高。
当数列元素不是整数，不适合计数排序。
如果数列中的元素都是小数，比如1.2，2.2，0.223，0.4，则无法创建对应的统计数组，这样显然无法进行计数排序。
数列最大值最小值的差距小，并且数据都是整数的时候，适合使用计数排序。