排序算法 —— 计数排序
引言
计数排序是桶排序思想的一种具体实现，针对一些具有特殊限制的样本数据，如公司员工年龄，那么样本数据本身就一定在0~200之间，针对这样的数据，使用从0到200 的桶数组，桶的位置已经是有序的，只需要将对应年龄的数据放入对应的桶，比如，24岁的员工有10人，那么就往 24 号桶中放10个数据。将所有员工年龄数据放入桶数组中后，只需要再次将它们放回到原数组就可以实现排序了：
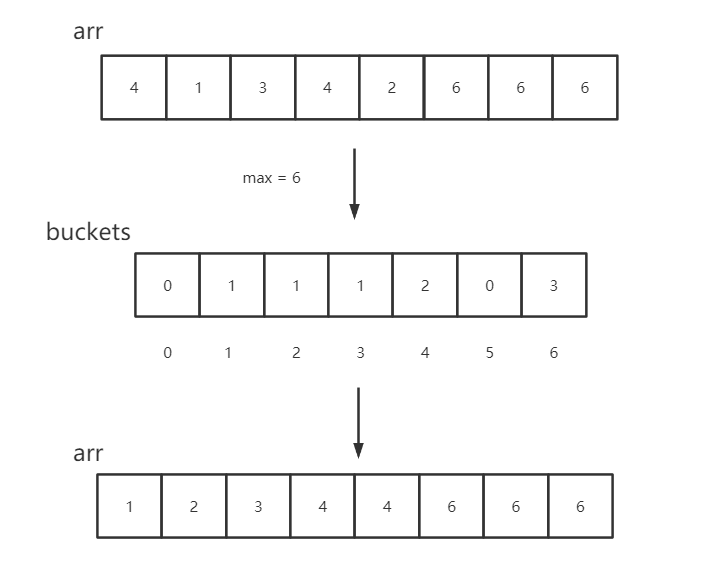
一、代码实现
public static void countSort(int[] arr) {if (arr == null || arr.length < 2)return;// 找到数组中的最大值int max = Integer.MIN_VALUE;for (int i = 0; i < arr.length; i++) {max = Math.max(max, arr[i]);}// 为了能够覆盖到最后一个值，需要+1int[] buckets = new int[max + 1];// 桶的下标记录数据，桶中的元素记录数据数量for (int i = 0; i < arr.length; i++) {buckets[arr[i]]++;}int i = 0;// 循环桶数组for (int j = 0; j < buckets.length; j++) {// 如果桶中有元素，那么执行放回操作，并递减，直到取出所有元素while (buckets[j]-- > 0) {// 桶下标代表数据本身，因此直接以下标作为返回的数据arr[i++] = j;}}}
二、计数排序的时间复杂度
计数排序是多个循环操作的累加。
首先是遍历数组，求得一个最大值，来决定桶的个数，时间复杂度是O(N)；
然后是将所有元素计数到辅助的桶数组中，时间复杂度是O(N);
随后，通过遍历桶数组，选出存有数据的桶，并依次取出累计个数的元素并返回到原数组中，虽然for循环嵌套了while循环，但实际上while只是把桶中的元素全部取出，其for + while操作的次数一定等于元素个数N，因此时间复杂度同样是O(N)。
所以，最后得出计数排序的时间复杂度是 O(N) + O(N) + O(N) = O(3N) 忽略倍数即为 O(N)。
柔光的暖阳◎
朱雀
我就是我
小鱼儿
![[C++] Value Categories](https://image.dandelioncloud.cn/images/20221021/aa4437ac757247c392f9012b5392f03e.png "[C++] Value Categories")
还没有评论，来说两句吧...