EM算法
Maximum Likelihood Estimation
Maximum Likelihood Estimation(MLE)是要选择一个最佳参数θ*，使得从训练集中观察到和情况出现的概率最大。即模型：
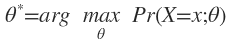
举例来说明。如下图
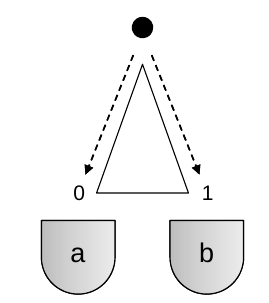
一个小黑球沿着一个三角形的木桩滚入杯子a或b中，可建立一个概率模型，由于是二值的，设服从Bernoulli分布，概率密度函数为：
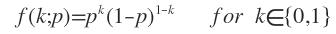
p是k=0的概率，也是我们要使用MLE方法要确定的参数。
在上面的滚球实验中，我们令Y是待确定的参数，X是观察到的结果。连续10次实验，观察到的结果是X=（b,b,b,a,b,b,b,b,b,a）。小球进入a杯的概率为p，则满足10次实验的联合概率为：
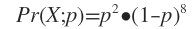
为了使X发生的概率最大，令上式一阶求导函数为0，得p=0.2。
含有隐含变量的弹球实验
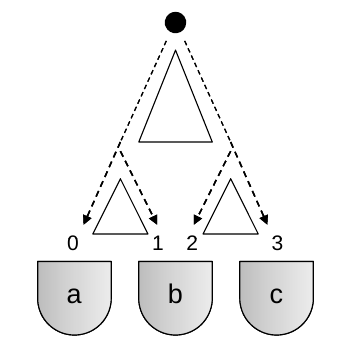
如上图，现在又多了两块三角形木桩，分别标记序号为0，1，2。并且实验中我们只知道小球最终进入了哪个杯子，中间的路线轨迹无从得知。
X取值于{a,b,c}表示小球进入哪个杯子。Y取值于{0,1,2,3}表示小球进入杯子前最后一步走的是哪条线路。小球在3个木桩处走右边侧的概率分别是p=(p0,p1,p2)。跟上例中一样，X表示训练集观测到的值，p是模型参数，而这里的Y就是”隐含变量”。
假如我们做了N次实验，小球经过路径0,1,2,3的次数依次是N0,N1,N2,N3，则：
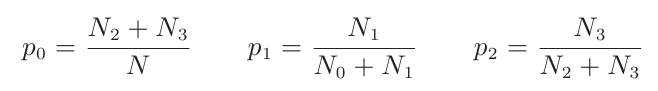
带隐含变量的MLE
现在我们来考虑这个概率模型：Pr(X,Y;θ)。只有X是可观察的，Y和θ都是未知的。
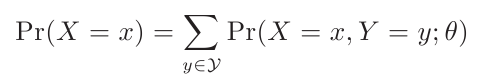
经过一组实验，我们观察到X的一组取值x=(x1,x2,…,xl)，则联合概率为：
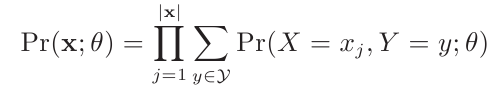
MLE就是要求出最佳的参数θ*，使得：
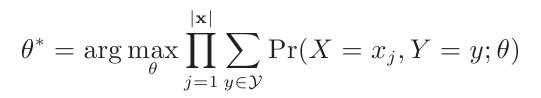
这个时候要求θ*，”令一阶求函数等于0“的方法已经行不通了，因为有隐含变量Y的存在。实现上上式很难找到一种解析求法，不过一种迭代的爬山算法可求解该问题。
Expectation Maximization
EM是一种迭代算法，它试图找到一系列的估计参数θ(0),θ(1),θ(2),….使得训练数据的marginal likelihood是不断增加的，即：
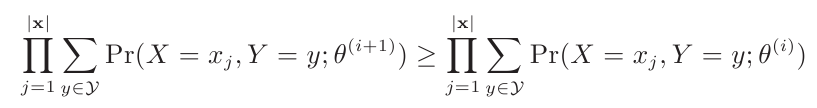
算法刚开始的时候θ(0)赋予随机的值，每次迭代经历一个E-Step和一个M-Step，迭代终止条件是θ(i+1)与θ(i)相等或十分相近。
E-Step是在θ(i)已知的情况下计算X=x时Y=y的后验概率：
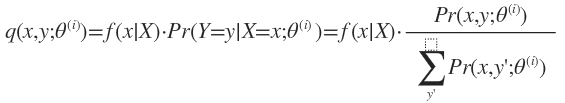
f(x|X)是一个权值，它表示观测值x在所有观察结果X中出现的频率。
M-Step：
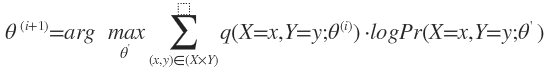
其中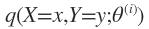
在E-Step已经求出来了。这时候可以用“令一阶导数等于0”的方法求出θ’。
EM算法收敛性的证明需要用到Jensen不等式，这里略去不讲。
举例计算
就拿上文那个3个木桩的滚球实验来说，做了N次实验，滚进3个杯子的次数依次是Na,Nb,Nc。
先给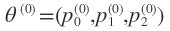
赋予一个随机的值。
E-Step:
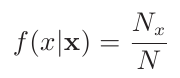
同时我们注意到
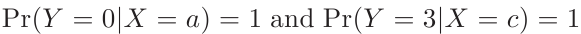
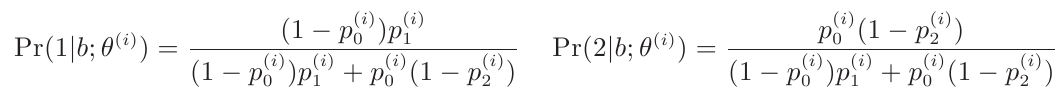
其它情况下Y的后验概率都为0。
M-Step:
我们只需要计算非0项就可以了
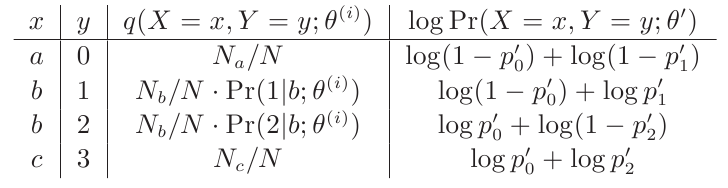
上面的每行第3列和第4列相乘，最后再按行相加，就得到关于θ(i+1)的函数，分别对p0,p1,p2求偏导，令导数为0，可求出p’0,p’1,p’2。
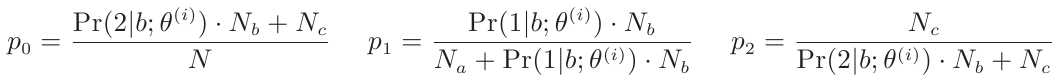
这里补充一个求导公式：
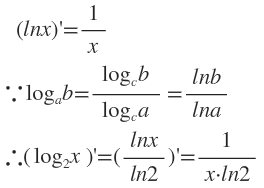
我们这个例子非常简单，计算θ(1)已经是最终的解了，当然你要计算出θ(2)才下此结论。
结束语
对于一般的模型，EM算法需要经过若干次迭代才能收敛，因为在M-Step依然是采用求导函数的方法，所以它找到的是极值点，即局部最优解，而非全局最优解。也正是因为EM算法具有局部性，所以它找到的最终解跟初始值θ(0)的选取有很大关系。
在求解HMM的学习问题、确立高斯混合模型参数用的都是EM算法。
快来打我*
我就是我
小灰灰
小鱼儿
还没有评论，来说两句吧...