Batch Normalization原理理解与Tensorflow实现

快来打我* 2023-07-14 13:56 72阅读 0赞

一、原始神经网络层和Internal Covariate Shift问题

在原始DNN中，隐藏层（HiddenLayer）将输入x通过系数矩阵W相乘得到线性组合z=Wx，再通过激活函数a=f(z)，得到隐藏层的输出a（X可以为输入层输入或者上一个隐藏层的输出）,具体结构如下：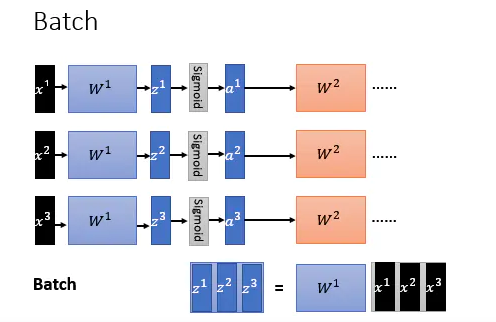
在这里插入图片描述
图中为一个批次(batch)的样本在隐藏层的传播过程。由于批次的不断传入和训练，DNN内部参数在不断改变，导致每一次隐藏层的输入分布不一致，这不符合机器学习中的IID假设（独立同分布假定）。也就是在训练过程中，隐层的输入分布老是变来变去，这就产生了内部协变量偏移问题(Internal Covariate Shift).

二、Batch Normalization

针对上面的协变量偏移问题，Google于2015年提出了Batch Normalization算法（BN）。BN通过对隐藏层线性组合输出z=Wx进行正态标准化z’=normalization(z)，再对标准化的输出z’进行尺度放缩和平移变换，使隐藏层的输出分布一致（注意：针对z=Wx进行标准化，而不是通过激活函数a=f(z)进行标准化）。
具体的Batch Normalization如下：
在这里插入图片描述
带有Batch Normalization处理的隐藏层结构如下：
在这里插入图片描述
其中参数γ和β是可以通过训练得到的。而在训练中μ和σ为该batch数据z的均值和方差。在预测时，μ和σ分别使用每个batch的μ和σ的加权并平均，其中起始输入的batch的权重较低，后面输入的batch的权重较高。

二、Batch Normalization的优点

BN可以把隐层神经元激活输入z=WX从变化不拘一格的正态分布拉回到了均值为0，方差为1的正态分布。使得隐藏层的输入分布一致，这解决了前面的协变量偏移问题(Internal Covariate Shift)。
同时，激活函数恰恰在中间区域的梯度是最大的，由于模型使用随机梯度下降(SGD)，这使得模型的训练使不会出现梯度弥散或者梯度忽大忽小的问题，同时参数的收敛速度更快。
在这里插入图片描述
具体总结的优点如下：

  1. 解决内部协变量偏移 (Internal Covariate Shift)
  2. 模型收敛加速
  3. 解决梯度弥散问题 (gradient vanish)
  4. 使模型具有正则化效果(个人感觉主要是因为训练时每一个batch的均值方差都不同，参数会去尽量适应这种不同，提高鲁棒性，防止过拟合。)
  5. 参过程简单，对于初始化要求没那么高

二、Batch Normalization的实现

本文Batch Normalization的实现参考Tensorflow Batch normalization函数
Tensorflow中实现Batch Normalization常用的有三种方法：

  1. tf.nn.batch_normalization： 是一个低级的操作函数，调用者需要自己处理张量的平均值和方差。
  2. python3 tf.layers.batch_normalization：是对先前操作的高级包装。最大的不同在于它负责创建和管理运行张量的均值和方差，并尽可能地调用快速融合运算。通常，这个函数应该是你的默认选择。
  3. python3 tf.contrib.layers.batch_norm：是 batch norm 的早期实现，其升级的核心API版本为（tf.layers.batch_normalization）。不推荐使用它，因为它可能会在未来的版本中丢失。

BN在使用时有几个注意事项：一般在非线性激活之前使用；在训练和测试的时候，用法不一样，在训练时由于BN的参数需要训练，需要设置training=True，在预测时参数已经训练好，此时设置training=True
python3 tf.layers.batch_normalization与python3 tf.contrib.layers.batch_norm调用方法相近。本文针对 tf.nn.batch_normalization和python3 tf.layers.batch_normalization进行讲解。

  1. tf.nn.batch_normalization
    在训练时，通过滑动平均值来计算每个batch_size的统计量（均值和方差）。
    在测试时，直接使用训练过程中保存的均值和方差。

    def batch_norm(x, name_scope, training, epsilon=1e-3, decay=0.99):

    1. """ Assume 2d [batch, values] tensor"""
    2. with tf.variable_scope(name_scope):
    3.     size = x.get_shape().as_list()[1]  #获得x维度
    4.     scale = tf.get_variable('scale', [size],initializer=tf.constant_initializer(0.1))
    5.     offset = tf.get_variable('offset', [size])
    7.     pop_mean = tf.get_variable('pop_mean', [size], initializer=tf.zeros_initializer(), trainable=False)   #均值定义，定义为不可训练
    8.     pop_var = tf.get_variable('pop_var', [size], initializer=tf.ones_initializer(), trainable=False)  #方差定义，定义为不可训练
    9.     batch_mean, batch_var = tf.nn.moments(x, [0])  #计算x的均值可方差
    10.     train_mean_op = tf.assign(pop_mean, pop_mean*decay+batch_mean*(1-decay))  #利用动量Momentum的思想，加权平均将pop_mean*decay+batch_mean*(1-decay)赋值给pop_mean ，求出新的pop_mean 
    11.     train_var_op = tf.assign(pop_var, pop_var*decay + batch_var*(1-decay))  #利用动量Momentum的思想，求出新的pop_var
    13.     def batch_statistics():
    14.         #模块内操作依赖于train_mean_op，train_var_op，只有这两个操作完成才能进行下面操作
    15.         with tf.control_dependencies([train_mean_op, train_var_op]):   
    16.             return tf.nn.batch_normalization(x, batch_mean, batch_var, offset, scale, epsilon)  #训练时使用，通过前面人为的batch_mean，batch_var进行batch_normalization
    18.     def population_statistics():
    19.         return tf.nn.batch_normalization(x, pop_mean, pop_var, offset, scale, epsilon)  #预测时使用，将确定好的pop_mean, pop_var对x进行BN
    21. #根据training判断是训练还是预测，训练时使用batch_statistics，预测时使用population_statistics。tf.cond(is_true,f1,f2)如果is_true=True，则执行函数f1，否则执行函数f2
    22. return tf.cond(training, batch_statistics, population_statistics)

  2. tf.layers.batch_normalization
    tf.layers.batch_normalization()一行搞定！设training为一个feed的布尔值变量，在训练和测试时feed不同的值。在训练时，要把计算得到的均值和方差保存下来，方便测试时使用。下面使一个卷积神经网络结合BN进行讲解

    with tf.variable_scope(‘layer1-conv1’):

    1. conv1_w = tf.get_variable('weight', [3, 3, 1, 32], initializer=tf.truncated_normal_initializer(stddev=0.1))
    2. conv1_b = tf.get_variable('bias', [32], initializer=tf.constant_initializer(0.0))
    3. conv1 = tf.nn.conv2d(input_tensor, conv1_w, strides=[1, 1, 1, 1],padding='SAME')  #卷积运算
    5. # 卷积操作
    6. res1 = tf.nn.bias_add(conv1, conv1_b)  #加偏置项
    7. # BN的输入是卷积结果，训练时training=True
    8. bn1 = tf.layers.batch_normalization(res1, training=is_train)
    9. # BN后再进行非线性激活
    10. relu1 = tf.nn.relu(bn1)

    训练时

    with tf.name_scope(‘train_op’):

    1. #将tf.GraphKeys.UPDATES_OPS保存在update_ops中，方便后面预测时直接提取
    2. update_ops = tf.get_collection(tf.GraphKeys.UPDATES_OPS)
    3. with tf.control_dependencies(update_ops):
    4.     #定义优化器
    5.     train_op = tf.train.AdamOptimizer(learning_rate).minimize(loss)

    进行训练

    training = tf.placeholder(tf.bool)
    feed_dict = {

    1. x:batch_x, y:batch_y, training:True}  #training设置为True

    预测时

    training = tf.placeholder(tf.bool)
    feed_dict = {

    1. x:batch_x, y:batch_y, training:False} #training设置为False

发表评论

表情：
评论列表 （有 0 条评论，72人围观）

还没有评论，来说两句吧...

相关阅读