差分约束系统-蒲公英云

参考博客：https://blog.csdn.net/dragon60066/article/details/80245797
此知识点需对最短路，最长路有了解。
差分约束系统应用一，
知道形如下面的不等式组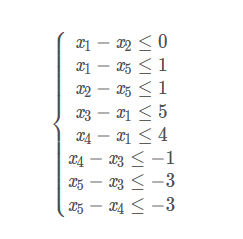
在这里插入图片描述
现在我们要求一组解x1=a1,x2=a2，这样的解来满足上面不等式组。
有一个性质，我们可以知道，如果有一组解x1=a1,x2=a2~~满足上面不等式组，那么这组解全部+d。即x1=a1+d,x2=a2+d，也是可满足的。因为做差之后d会被抵消掉。
现在，我们分析一个不等式
x1-x2<=k 转化为x1<=x2 +k在转化x2>=x1-k;
此不等式是不是很眼熟呢。我们回忆在最短路的学习中，是不是有dis[v] >=dis[u] + k;这个不等式组呢。此不等式组在最短路中的意义为:
到v的最短路>=到u的最短路+（u到v的比边权）。
我们可以注意到u到v的边权为k。
那么我们是不是可以像最短路一样，
给x1到x2连上一条边权为-k的边呢。
我们通过此种建图之后，如何继续判断是否存在一组解满足不等式组呢？
我们综合最短路的应用，我们是不是可以跑最短路spfa算法，来判断，该图中是否存在负环，如果存在负环，那么一定是无解的。
存在负环的情况为:a>b,b>c,c>a。可画图，就可以理解为何存在负环不行。

例题：https://www.luogu.com.cn/problem/P1993

#include"stdio.h"
#include"string.h"
#include"algorithm"
using namespace std;
const int N = 100100;
const int INF = 1e9 + 7;
int n,m,ans;
int head[N],ver[N * 10],Next[10 * N],edge[N * 10],tot;
int vis[N],dist[N];
void add(int x,int y,int w){
    ver[++ tot] = y; edge[tot] = w;
    Next[tot] = head[x]; head[x] = tot;
}
void dfs(int x){
    vis[x] = 1;
    for(int i = head[x]; i; i = Next[i])
    {
        int y = ver[i],w = edge[i];
        if(dist[y] > dist[x] + w){
            if(vis[y] || ans) {ans = 1;break;}
            dist[y] = dist[x] + w;
            dfs(y);
        }
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 1; i <= n; i ++)
        dist[i] = INF;
    for(int i = 1; i <= m; i ++)
    {
        int op; scanf("%d",&op);
        if(op == 3) {
            int x,y; scanf("%d%d",&x,&y);
            add(x,y,0); add(y,x,0);
        } else if(op == 1){
            int x,y,w; scanf("%d%d%d",&x,&y,&w);
            add(x,y,-w);
        } else {
            int x,y,w; scanf("%d%d%d",&x,&y,&w);
            add(y,x,w);
        }
    }
    ans = 0;
    for(int i = 1; i <= n; i ++){
        memset(vis,0,sizeof(vis));
        dfs(i);
        if(ans) break;
    }
    if(ans == 1) printf("No\n");
    else printf("Yes\n");
}

例题二：https://www.luogu.com.cn/problem/P3275
参考题解：https://www.luogu.com.cn/problemnew/solution/P3275
从题目中，我们可以得到所有的小朋友一定会分到一个糖果。
同时，题目要求的是最小需要多少个糖果才能满足需求。
我们现在建图时，建（u，v，w）这条边表示顶点v比顶点u大w。
我们观察5种需求类型，
第一种，a==b，add(u,v,0);add(v,u,0);
第二种，a=b add(b,a,0)//如果a>=b，那么同样根据贪心原则，我肯定是让他们越靠近越好。
第四种，a>b add(b,a,1);
第五种，a<=b add(a,b,0);
那么我们建图之后就跑最长路即可。
如下图，

3到1的路径为1，但是因为2的限制，所以1要比3大2。
同时，在跑spfa的时候判正权环的出现。
正权环即：
1->2 w 2
2->3 w 3
3->1 w 3
如果在此图上跑最长路，那么我们将会一直跑下去，不能结束，所以要判断正权环。

#include"stdio.h"
#include"string.h"
#include"queue"
#include"algorithm"
using namespace std;
typedef long long ll;
inline int read(){
int a=0;char x=getchar();
while(x<'0'||x>'9')x=getchar();
while(x>='0'&&x<='9')a=(a<<3)+(a<<1)+x-48,x=getchar();
return a;
}
const int N = 300100,M = 1001010;
int head[N],ver[M],Next[M],edge[M],tot;
int n,k,dist[N],vis[N];
int cnt[N];
void add(int x,int y,int w){
ver[++ tot] = y; Next[tot] = head[x];
edge[tot] = w; head[x] = tot;
}
bool bfs()
{
queue<int> Q; Q.push(0);
dist[0] = 0;vis[0] = 1;
while(!Q.empty())
{
int x = Q.front(); Q.pop();
vis[x] = 0;
cnt[x] ++;
if(cnt[x] >= n){
return false;
}
for(int i = head[x]; i; i = Next[i]){
int y = ver[i],w = edge[i];
if(dist[y] < dist[x] + w){
dist[y] = dist[x] + w;
if(vis[y] == 0){
vis[y] = 1; Q.push(y);
}
}
}
}
return true;
}
int main()
{
n = read(); k = read();
for(int i = 1; i <= k; i ++)
{
int op,a,b;
op = read(); a = read(); b = read();
if(op == 1) add(a,b,0),add(b,a,0);
else if(op == 2) add(a,b,1);
else if(op == 3) add(b,a,0);
else if(op == 4) add(b,a,1);
else add(a,b,0);
if(op == 2 || op == 4)
{
if(a == b) {printf("-1\n"); return 0;}
}
}
for(int i = n; i >= 1; i --)add(0,i,1);
if(bfs() == false){
printf("-1\n");
} else
{
ll ans = 0;
for(int i = 1; i <= n; i ++) ans += (ll)dist[i];
printf("%lld\n",ans);
}
}
：
例题三：https://www.cnblogs.com/five20/p/9173155.html
例题：https://www.luogu.com.cn/problem/P2294
很容易的想到建图方式：
w[u,v] = k,表示v大u，k个单位。
同时隐含着w[v,u] = -k。这一条件。
把这两个图建出来，发现，如果有环，那就不合法。

#include"stdio.h"
#include"string.h"
#include"queue"
#include"algorithm"
using namespace std;
typedef long long ll;
inline int read(){
int a=0;char x=getchar();bool f=0;
while((x<'0'||x>'9')&&x!='-')x=getchar();
if(x=='-')x=getchar(),f=1;
while(x>='0'&&x<='9')a=(a<<3)+(a<<1)+x-48,x=getchar();
return f?-a:a;
}
const int N = 300100,M = 1001010;
const int INF = 1000000100;
int head[N],ver[M],Next[M],edge[M],tot;
int n,k,dist[N],vis[N];
int cnt[N];
void add(int x,int y,int w)
{
ver[++ tot] = y;
Next[tot] = head[x];
edge[tot] = w;
head[x] = tot;
}
bool bfs(int x)
{
queue<int> Q;
Q.push(x);
for(int i = 0; i <= n; i ++) dist[i] = -INF;
dist[x] = 0;
vis[x] = 1;
while(!Q.empty())
{
int x = Q.front();
Q.pop();
vis[x] = 0;
cnt[x] ++;
if(cnt[x] >= n)
{
return false;
}
for(int i = head[x]; i; i = Next[i])
{
int y = ver[i],w = edge[i];
if(dist[y] < dist[x] + w)
{
dist[y] = dist[x] + w;
if(vis[y] == 0)
{
vis[y] = 1;
Q.push(y);
}
}
}
}
return true;
}
void init()
{
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
memset(cnt,0,sizeof(cnt));
tot = 0;
}
int main()
{
int T;
T = read();
while(T --)
{
init();
n = read();
k = read();
for(int i = 1; i <= k; i ++)
{
int a,b,w;
a = read(); b = read();w = read();
add(a - 1,b,w); add(b,a - 1,-w);
}
int mark = 1;
for(int i = 0; i <= n; i ++){
if(cnt[i] == 0){
if(bfs(i) == false) {mark = 0;break;}
}
}
if(mark == 1) printf("true\n");
else printf("false\n");
}
return 0;
}