二叉查找树 (二叉排序树)，C语言实现-蒲公英云

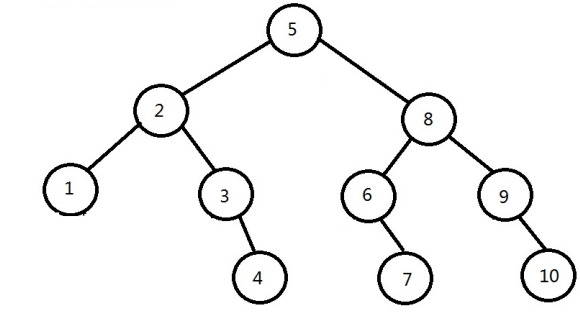
在这里插入图片描述
如果有上面这样一棵二叉树，它满足左儿子的值 ≤ 父亲的值＜右儿子的值这样一个规则，我们来尝试从这棵二叉树中查找是否存在一个元素，该元素的值是7。从这棵二叉树的根节点 (5) 开始查找：
第一步、7 > 5，所以继续查找5的右儿子；
第二步、7 < 8，所以继续查找4的左儿子；
第三步、7 > 6，所以继续查找6的右儿子；
第四步、7 == 7，找到元素7。
在10个元素中查找元素，一共查找了4次，而且最多只需要查找4次。也就是说，即使在最差的情况下，也只需要查找logN次即可找到目标元素，即查找的时间复杂度为O(logN)。这个查找效率与二分查找是一样的。

我们已经知道二分查找了，为什么还需要学习这样的树状结构呢？原因是二分查找一般用于有序数组中的元素的查找，而数组的空间大小是固定的，不能任意插入数据，如果有一个足够大空间的数组，往一个有序数组中插入 (删除) 数据，而且在插入 (删除) 数据后该数组仍然保持有序，那么插入 (删除) 数据的时间复杂度为O(N)。显然，这样的效率是不能让人满意的。而我们这里的树状结构———二叉查找树，则可以动态插入 (删除) 数据，插入 (删除) 数据的时间复杂度为O(logN)，而且我们可以用动态添加结点，而不需要事先申请很大的内存空间。

3.1 二叉查找树的查

因为二叉查找树满足左儿子的值 ≤ 父亲的值＜右儿子的值这个规则，所以在查找二叉树中查找一个元素就变得很简单：
如果要查找的元素与根节点相等，就返回；
如果要查找的元素比根节点大，那就继续在根节点的右儿子结点上递归查找；
如果要查找的元素比根节点小，那就继续在根节点的左儿子结点上递归查找；
递归的出口一共有两个：一个是找到后返回，另一个是确定找不到要找的元素后返回-1

int find(struct Node *root, int n) //从根节点开始查找一个结点。
{
    if (root == NULL) //递归的出口1
    {
        return -1; //找不到就返回-1 
    }
    //递归的出口2
    if(root->data == n) //找到就返回 
    {
        return n;
    }
    else if(n > root->data) //如果n > root->data，就从这个结点的右儿子继续查找
    {
        return find(root->rightSon, n); //递归查找
    }
    else //如果n <= root->data，就从这个结点的左儿子继续查找
    {
        return find(root->leftSon, n); //递归查找
    }
}

3.2 二叉查找树的增

因为二叉查找树满足左儿子的值 ≤ 父亲的值＜右儿子的值这个规则，所以在查找二叉树中增加一个元素就变成为要增加的元素找到一个合适的位置，然后在这个位置上添加一个结点。而找到一个合适的位置的代码与查找一个元素的代码很相似：

void addNode(struct Node **root, int data) //增加一个结点
{
    struct Node * temp = createNode(data); //先新建一个结点 
    struct Node * rr = NULL; //根节点 
    if (*root == NULL) //不需要判断root == NULL
    {
        //如果一棵树还没有root，则首先要生成root
        *root = temp;
    }
    //如果有root了，则在root下添加结点。用指针方式 
    else // root != NULL
    {
        rr = *root; 
        //如果data比root的值小，且没有左孩子，则让temp成为root的左孩子
        if (data < rr->data && rr->leftSon == NULL)
        {
            rr->leftSon = temp;
        }
        //如果data比root的值大，且没有右孩子，则让temp成为root的右孩子
        else if (data > rr->data && rr->rightSon == NULL)
        {
            rr->rightSon = temp;
        }
        //剩余的情况是data比root的值小，且root有左孩子
        //data比root的值大，且root有右孩子
        //这两种情况下，都要递归，但是仍然要分两种情况进行递归
        else if (data < rr->data)
        {
            addNode(&rr->leftSon, data); // 递归
        }
        else
        {
            addNode(&rr->rightSon, data); // 递归
        }
        *root = rr; //修改root 
    }
}

3.3 二叉查找树的改

二叉查找树主要是用来增加、删除和查找元素的。如果对一个结点进行简单的修改，则很容易导致不符合左儿子的值 ≤ 父亲的值＜右儿子的值这个规则。所以二叉查找树中不设置修改功能。

3.4 二叉查找树的删

因为二叉查找树满足左儿子的值 ≤ 父亲的值＜右儿子的值这个规则，所以二叉查找树的增加和查找都非常简单。但是同样因为这个规则，二叉查找树的删除功能却比较复杂。下面分情况进行讨论：
① 被删除的结点没有儿子：从父节点直接删除这个结点即可。
② 被删除的结点只有一个左儿子。把父节点的儿子结点指向被删除的结点的儿子接口。
③ 被删除的结点只有一个右儿子。与②的操作相似。
④ 被删除的结点有2个儿子。把左儿子递归的放到右儿子下面。然后把父节点指向右儿子。这四种情况下都要区分被删除的结点是父节点的左儿子还是右儿子。所以一共是8种情况。

我们先写出找父节点的函数。注意，返回值是指针：

struct Node * getFatherNode(struct Node *root, int n)
{
    //根节点为NULL或根节点的值==n
    if(root == NULL || root->data == n)
    {
        return NULL; //找不到父节点，返回NULL 
    }
    //已经到了叶子节点了，仍然没有找到 
    if(root->leftSon == NULL && root->rightSon == NULL)
    {
        return NULL;//找不到了，返回NULL 
    }
    //如果根节点的值比n大，同时左子树不是NULL 
    if(root->data > n && root->leftSon != NULL)
    {
        //如果左儿子的值 == n，说明根节点就是要找的结点 
        if(root->leftSon->data == n)
        {
            return root;//返回根节点
        }
        return getFatherNode(root->leftSon, n); //在左子树中递归查找 
    }
    //如果根节点的值比n小，同时右子树不是NULL
    if(root->data < n && root->rightSon != NULL)
    {
        //如果右儿子的值 == n，说明根节点就是要找的结点
        if(root->rightSon->data == n)
        {
            return root; //返回根节点 
        }
        return getFatherNode(root->rightSon, n); //在右子树中递归查找
    }
}

接着，我们要判断父节点与被删除的结点之间的关系。根据父节点和子节点的index，确定子节点是不是父节点的左儿子：

int isLeftSon(struct Node *root, struct Node fatherNode, struct Node sonNode)
{
    //如果父节点的左儿子不存在，或者左儿子存在，但左儿子的值与sonNode不相等 
    if(fatherNode.leftSon == NULL || fatherNode.leftSon->data != sonNode.data)
    {
        return 0; //不是左儿子就返回0
    }
    return 1; //是左儿子就返回1
}

有了上面两个方法，我们就可以进行删除操作了。8种情况，一一讨论 -：

void deleteNode(struct Node **root, int n)
{
    struct Node *r = *root; //二级指针换成一级指针 
    struct Node *node = findNode(r, n); //找到指定结点 
    struct Node *fatherNode = getFatherNode(r, n); //找到父节点 
    if(node == NULL) //如果找不到要删除的结点，则返回 
    {
        return;
    }
    //第一种情况：被删除的结点没有子节点。
    //一定要用指针的方式，不能用struct Node变量。否则修改了不能影响原来的数据 
    if(node->leftSon == NULL && node->rightSon == NULL) 
    {
        if(isLeftSon(r, *fatherNode, *node)) //如果被删除的结点是父节点的左儿子 
        {
            fatherNode->leftSon = NULL; //父节点的左儿子的指针设为NULL即可 
        }
        else //如果被删除的结点是父节点的右儿子
        {
            fatherNode->rightSon = NULL; //父节点的右儿子的指针设为NULL即可
        }
    }
    //第二种情况: 被删除的结点只有一个左儿子 
    else if(node->leftSon != NULL && node->rightSon == NULL)
    {
        if(isLeftSon(r, *fatherNode, *node)) //如果被删除的结点是父节点的左儿子
        {
            fatherNode->leftSon = node->leftSon; //父节点的左儿子指向删除结点的左儿子 
        }
        else //如果被删除的结点是父节点的右儿子
        {
            fatherNode->rightSon = node->leftSon;//父节点的右儿子指向删除结点的左儿子
        }
    }
    //第三种情况: 被删除的结点只有一个右儿子 
    else if(node->leftSon == NULL && node->rightSon != NULL)
    {
        if(isLeftSon(r, *fatherNode, *node)) //如果被删除的结点是父节点的左儿子
        {
            //父节点的左儿子指向删除结点的右儿子 
            fatherNode->leftSon = node->rightSon;         
        }
        else //如果被删除的结点是父节点的右儿子
        {
            //父节点的右儿子指向删除结点的右儿子
            fatherNode->rightSon = node->rightSon;         
        }
    }
    //第四种情况：被删除的结点有两个儿子
    //让左儿子变成右儿子的儿子，甚至孙子。(递归) 
    else 
    {
        struct Node *myLeftSon = node->leftSon;
        struct Node *myRightSon = node->rightSon;
        addNode(&myRightSon, myLeftSon->data); //递归，把左儿子加到右儿子下面 
        node->leftSon = NULL; //node的左儿子就可以删掉了 
        if(isLeftSon(r, *fatherNode, *node)) //如果被删除的结点是父节点的左儿子
        {
            fatherNode->leftSon = myRightSon; //父节点的左儿子指向删除结点的右儿子
        }
        else //如果被删除的结点是父节点的右儿子
        {
            fatherNode->rightSon = myRightSon; //父节点的右儿子指向删除结点的右儿子
        }
    } 
    free(node); //不要忘记释放指针，回收内存 
    *root = r; //应用到root，用一级指针对二级指针进行赋值 
}
下面是二叉查找树的增加、删除、查找、遍历 (先序、中序和后续) 的完整代码：
```c
#include <stdio.h>
#include <stdlib.h>
struct Node // 定义一个节点，这是一颗二叉树
{
    int data; //一个结点的值 
    struct Node * leftSon; //结点的左孩子 
    struct Node * rightSon; //结点的右孩子 
};
//创建一个结点的方法
struct Node * createNode(int myData)
{
    struct Node *node;
    node = (struct Node *) malloc(sizeof(struct Node)); //手动申请内存 
    node->data = myData;
    node->leftSon = NULL; //一定要对两个孩子的指针进行初始化 
    node->rightSon = NULL; //一定要对两个孩子的指针进行初始化
    return node;
}
void addNode(struct Node **root, int data) //增加一个结点
{
    struct Node * temp = createNode(data); //先新建一个结点 
    struct Node * rr = NULL; //根节点 
    if (*root == NULL) //不需要判断root == NULL
    {
        //如果一棵树还没有root，则首先要生成root
        *root = temp;
    }
    //如果有root了，则在root下添加结点。用指针方式 
    else // root != NULL
    {
        rr = *root; 
        //如果data比root的值小，且没有左孩子，则让temp成为root的左孩子
        if (data < rr->data && rr->leftSon == NULL)
        {
            rr->leftSon = temp;
        }
        //如果data比root的值大，且没有右孩子，则让temp成为root的右孩子
        else if (data > rr->data && rr->rightSon == NULL)
        {
            rr->rightSon = temp;
        }
        //剩余的情况是data比root的值小，且root有左孩子
        //data比root的值大，且root有右孩子
        //这两种情况下，都要递归，但是仍然要分两种情况进行递归
        else if (data < rr->data)
        {
            addNode(&rr->leftSon, data); // 递归
        }
        else
        {
            addNode(&rr->rightSon, data); // 递归
        }
        *root = rr; //修改root 
    }
}
void preOrderTraverse(struct Node *root) //先序遍历二叉树
{
    if (root == NULL) //递归的出口 
    {
        return;
    }
    printf("%d ", root->data); //先序遍历就是把这个语句放在最前面 
    preOrderTraverse(root->leftSon); //递归访问 
    preOrderTraverse(root->rightSon); //递归访问
}
void inOrderTraverse(struct Node *root) //中序遍历二叉树
{
    if (root == NULL) //递归的出口
    {
        return;
    }
    inOrderTraverse(root->leftSon); //递归访问
    printf("%d ", root->data); //中序遍历就是把这个语句放在中间 
    inOrderTraverse(root->rightSon); //递归访问
}
void postOrderTraverse(struct Node *root) //后序遍历二叉树
{
    if (root == NULL) //递归的出口
    {
        return;
    }
    postOrderTraverse(root->leftSon); //递归访问
    postOrderTraverse(root->rightSon); //递归访问
    printf("%d ", root->data); //后序遍历就是把这个语句放在中间
}
//从根节点开始查找一个结点。
struct Node * findNode(struct Node *root, int n)
{
    if (root == NULL) //递归的出口1
    {
        return NULL; //找不到
    }
    //递归的出口2
    if(root->data == n) //找到就返回 
    {
        return root;
    }
    else if(n > root->data) //如果n > root->data，就从这个结点的右儿子继续查找
    {
        return findNode(root->rightSon, n); //递归查找
    }
    else //如果n <= root->data，就从这个结点的左儿子继续查找
    {
        return findNode(root->leftSon, n); //递归查找
    }
}
//找到指定结点的父节点，返回指针 
struct Node * getFatherNode(struct Node *root, int n)
{
    //根节点为NULL或根节点的值==n
    if(root == NULL || root->data == n)
    {
        return NULL; //找不到父节点，返回NULL 
    }
    //已经到了叶子节点了，仍然没有找到 
    if(root->leftSon == NULL && root->rightSon == NULL)
    {
        return NULL;//找不到了，返回NULL 
    }
    //如果根节点的值比n大，同时左子树不是NULL 
    if(root->data > n && root->leftSon != NULL)
    {
        //如果左儿子的值 == n，说明根节点就是要找的结点 
        if(root->leftSon->data == n)
        {
            return root;//返回根节点
        }
        return getFatherNode(root->leftSon, n); //在左子树中递归查找 
    }
    //如果根节点的值比n小，同时右子树不是NULL
    if(root->data < n && root->rightSon != NULL)
    {
        //如果右儿子的值 == n，说明根节点就是要找的结点
        if(root->rightSon->data == n)
        {
            return root; //返回根节点 
        }
        return getFatherNode(root->rightSon, n); //在右子树中递归查找
    }
}
//根据父节点和子节点的index，确定子节点是不是父节点的左儿子。 
int isLeftSon(struct Node *root, struct Node fatherNode, struct Node sonNode)
{
    //如果父节点的左儿子不存在，或者左儿子存在，但左儿子的值与sonNode不相等 
    if(fatherNode.leftSon == NULL || fatherNode.leftSon->data != sonNode.data)
    {
        return 0; //不是左儿子就返回0
    }
    return 1; //是左儿子就返回1
}
//二叉查找树的删除是最复杂的。需要考虑多种情况
void deleteNode(struct Node **root, int n)
{
    struct Node *r = *root; //二级指针换成一级指针 
    struct Node *node = findNode(r, n); //找到指定结点 
    struct Node *fatherNode = getFatherNode(r, n); //找到父节点 
    if(node == NULL) //如果找不到要删除的结点，则返回 
    {
        return;
    }
    //第一种情况：被删除的结点没有子节点。
    //一定要用指针的方式，不能用struct Node变量。否则修改了不能影响原来的数据 
    if(node->leftSon == NULL && node->rightSon == NULL) 
    {
        if(isLeftSon(r, *fatherNode, *node)) //如果被删除的结点是父节点的左儿子 
        {
            fatherNode->leftSon = NULL; //父节点的左儿子的指针设为NULL即可 
        }
        else //如果被删除的结点是父节点的右儿子
        {
            fatherNode->rightSon = NULL; //父节点的右儿子的指针设为NULL即可
        }
    }
    //第二种情况: 被删除的结点只有一个左儿子 
    else if(node->leftSon != NULL && node->rightSon == NULL)
    {
        if(isLeftSon(r, *fatherNode, *node)) //如果被删除的结点是父节点的左儿子
        {
            fatherNode->leftSon = node->leftSon; //父节点的左儿子指向删除结点的左儿子 
        }
        else //如果被删除的结点是父节点的右儿子
        {
            fatherNode->rightSon = node->leftSon;//父节点的右儿子指向删除结点的左儿子
        }
    }
    //第三种情况: 被删除的结点只有一个右儿子 
    else if(node->leftSon == NULL && node->rightSon != NULL)
    {
        if(isLeftSon(r, *fatherNode, *node)) //如果被删除的结点是父节点的左儿子
        {
            //父节点的左儿子指向被删除结点的右儿子
            fatherNode->leftSon = node->rightSon;  
        }
        else //如果被删除的结点是父节点的右儿子
        {
            //父节点的右儿子指向被删除结点的右儿子
            fatherNode->rightSon = node->rightSon; 
        }
    }
    //第四种情况：被删除的结点有两个儿子
    //让左儿子变成右儿子的儿子，甚至孙子。(递归) 
    else 
    {
        struct Node *myLeftSon = node->leftSon;
        struct Node *myRightSon = node->rightSon;
        addNode(&myRightSon, myLeftSon->data); //递归，把左儿子加到右儿子下面 
        node->leftSon = NULL; //node的左儿子就可以删掉了 
        if(isLeftSon(r, *fatherNode, *node)) //如果被删除的结点是父节点的左儿子
        {
            fatherNode->leftSon = myRightSon; //父节点的左儿子指向删除结点的右儿子
        }
        else //如果被删除的结点是父节点的右儿子
        {
            fatherNode->rightSon = myRightSon; //父节点的右儿子指向删除结点的右儿子
        }
    } 
    free(node); //不要忘记释放指针，回收内存 
    *root = r; //应用到root，用一级指针对二级指针进行赋值 
}
int main()
{
    struct Node *root = NULL;
    //添加的数据是无序的 
    addNode(&root, 4);
    addNode(&root, 1);
    addNode(&root, 3);
    addNode(&root, 2);
    addNode(&root, 5);
    addNode(&root, 7);
    addNode(&root, 6);
    addNode(&root, 0);
    addNode(&root, 8);
    int n = 2;
    struct Node *fatherNode = getFatherNode(root, n);
    printf("%d的父节点的编号：%d\r\n", n, fatherNode->data);
    struct Node * sonNode = findNode(root, n);
    printf("%d是%d的左儿子吗？%d", sonNode->data, fatherNode->data, isLeftSon(root, *fatherNode, *sonNode));
    printf("\r\n先序遍历: \r\n");
    preOrderTraverse(root);
    printf("\r\n\r\n中序遍历，可以得到有序的结果: \r\n");
    inOrderTraverse(root);
    int m = 3;
    deleteNode(&root, m);
    printf("\r\n\r\n删除结点%d之后进行中序遍历：\r\n", m);
    inOrderTraverse(root);
    printf("\r\n\r\n后序遍历: \r\n");
    postOrderTraverse(root);
    printf("\r\n\r\nHello\r\n");
    return 0;
}

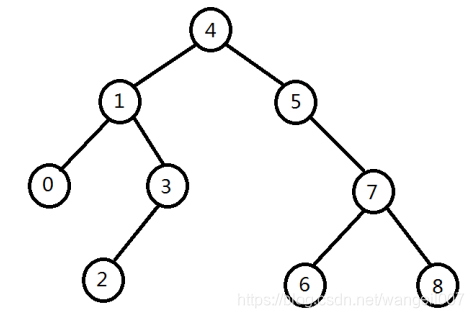
主函数中建立的二叉查找树的结构如下：

在这里插入图片描述

4 平衡二叉树 (AVL)

一个极端的情况，如果二叉查找树是左斜树或者右斜树，它也满足左儿子的值 ≤ 父亲的值＜右儿子的值。由于斜树实际上已经退化成链表了，对于这样的二叉查找树来说，查找、插入、删除元素的时间复杂度都会降低为O(N)。那么我们怎样避免二叉查找树退化成斜树呢？平衡二叉树可以就是为了解决这个问题而诞生的。
平衡二叉树：任意一个结点的左子树和右子树的高度都相等，或者相差1。这样的二叉排序树称之为平衡二叉树。在平衡二叉树中，查找、插入、删除元素的时间复杂度都是O(logN)。实现平衡二叉树的代码非常复杂，这里就不实现了。类似的结构有红黑树、SB树等。有兴趣的读者请自己查阅相关资料吧。