BF算法与KMP算法-蒲公英云

BF算法与KMP算法

墨蓝 2023-02-28 12:48 193阅读 0赞

BF算法与KMP算法都是用来查找主串中子串的位置，也就是模式匹配。
BF算法的简单粗暴，缺点是每趟匹配不成功时，存在大量回溯，导致程序效率低下，而KMP算法充分利用了成功匹配部分的结果，保证了主串游标不回溯，通过模式串向右滑动代替模式串游标回溯，大大提高了程序运行效率。
简单的了解了一下BF和KMP算法的作用和优缺点后，我们先来看一下具体的代码和细节

先看BF算法(这个算法比较简单，就不多说了直接上代码)

#include<iostream>
#include<string.h>
using namespace std;
int BF(char S[],char T[])
{
    int i=0, j=0,len1=strlen(S),len2=strlen(T);
   for(i;i<len1;i++)
   {
       if(S[i]==T[j])
        j++;
       else
       {
           i=i-j+1;
           j=0;
       }
       if(j==len2)return i-j+1;
   }
   return -1;
}
int main()
{
    char a[20],b[5];
    cin>>a>>b;
    cout<<BF(a,b);
}

关于KMP算法，主要的难点在于next数组的计算
在这之前，我们已经知道了主串指针i可以不回溯，模式串向右滑动到新的比较起点k，并且k仅与模式串T有关，
那么如何由当前部分匹配结果确定模式向右滑动的新比较起点k？
模式应该向右滑动多远才是效率最高的？
解决了这两个问题，next的计算也就简单了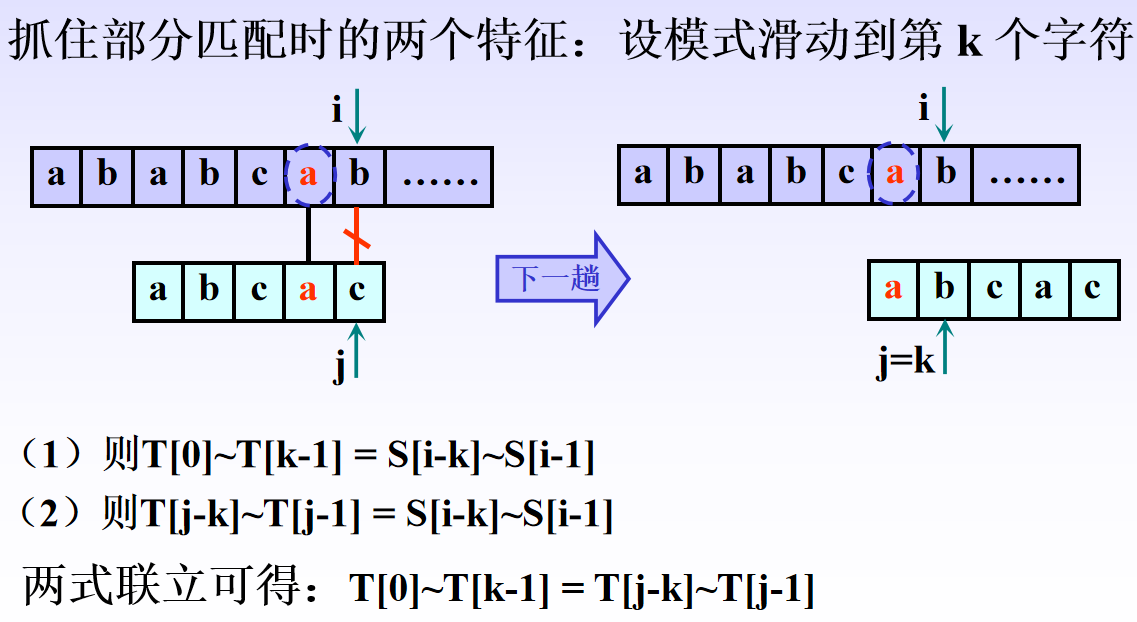 watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQ2NjAxMzM4_size_16_color_FFFFFF_t_70
这样，我们通过T[0]-T[K-1]=T[J-K]~T[J-1]可以确定每次匹配失败时应该回溯的位置k，而滑动多远才是效率最高的问题取k中最大值即可
接下来是具体的代码

#include<string>
#include<iostream>
using namespace std;
void Getnext(string t, int next[])
{
    int j = 0, k = -1;
    next[0] = -1;
    while (j < t.length() )
    {
        if (k == -1 || t[j] == t[k])
        {
            j++; k++;
            next[j] = k;
        }
        else k = next[k];
    }
}
int KMP(string p, string t)
{
    int i = 0, j = 0;
    int* next = new int[t.length()];
    Getnext(t, next);
    for (int i = 0; i < t.length(); i++)
        cout << next[i] << " ";
    cout << endl;
    while (i < p.length() && j < t.length())
    {
        if (p[i] != t[j])
        {
            j = next[j];//匹配失败，模式串向右滑动至next[j]（也就是之前说的k）
        }
        if (p[i] == t[j] || j == -1)
        {
            j++; i++;
        }
    }
    if (j >= t.length())return i - t.length();
    else return -1;
}
int main()
{
    string p = "DABCDDACBAEDABCFDABCDABD";
    string t = "DABCDABD";
    cout << " ";
    for (int i = 0; i < t.length(); i++)
        cout << t[i] << " ";
    cout << endl;
    cout<<KMP(p, t);
}