二叉树的非递归遍历和层次遍历详解-蒲公英云

二叉树非递归遍历非递归的后序遍历二叉树

//非递归的后续遍历二叉树  
void HXprint(Tree *tree){
    Stack s = initStack();   //初始化一个下面使用的栈 
    treeNode *p = tree;    //新建一个遍历指针 
    treeNode *r=NULL;    //辅助变量 
    cout<<"-------"<<endl;
    while(p||!isEmpty(s)){
        //当遍历变量和栈同时为空时  表示遍历完成 
        if(p){
       //p非空  就入栈  并且遍历指针更改为指向当前节点的左孩子 
            push(s,p);
            p = p->lchild;
        }else{
        //p为空  表示当前节点已经没有左孩子 
            p = getTop(s);   //获取栈顶元素   也就是最后一个入栈的结点 
            if(p->rchild && p->rchild!=r){
       //判断栈顶结点是否有右孩子  
                p=p->rchild;    //修改指针一直找右孩子  直到没有右孩子  或者 右孩子已经访问过 
            }else{
                p = pop(s);  //如果没有右孩子  或者  右孩子已经访问过了 就开始出栈栈顶元素   并且用指针p指向出栈元素
                cout<<p->data<<endl;    //输出当前指针指向的结点 
                r=p;      //将r修改为已经访问过的右孩子   防止再次访问到右孩子 
                p=NULL;   //将p修改为空指针 防止再次入栈 
            }
        }
    }
}

逻辑解释：
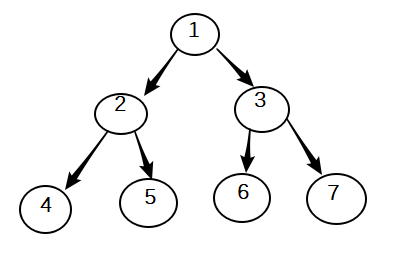
按照下图和上述代码
思考一下每一个结点都会经历入栈出栈那么遍历方法的结束就应该是，当所有的结点都已经访问过，并且当前的栈为空的时候表示所有的结点都已经输出于是有了如下循环
在这里插入图片描述循环开始的时候，p指针指向根节点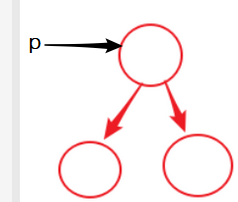循环三次后，应该是下图的样子
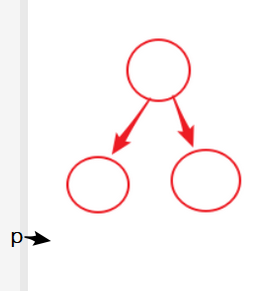而此时栈中应该入队了两个结点分别是根节点和它的左孩子结点
此时再次循环 p 为空 p指向栈顶元素如果过栈顶元素有右孩子右孩子入栈 p指向右孩子如果没有则输出根节点的左孩子结点此时再次将p指针修改为 null 这个时候栈中只有一个根节点并且 p结点指向空
再次进入循环 p指向栈顶 p这时有右孩子则将右孩子入栈修改辅助指针r指向右孩子再次进入循环出栈输出元素便是输出的右孩子元素最后输出的是根节点元素
大家可以根据下图分别进行一遍推演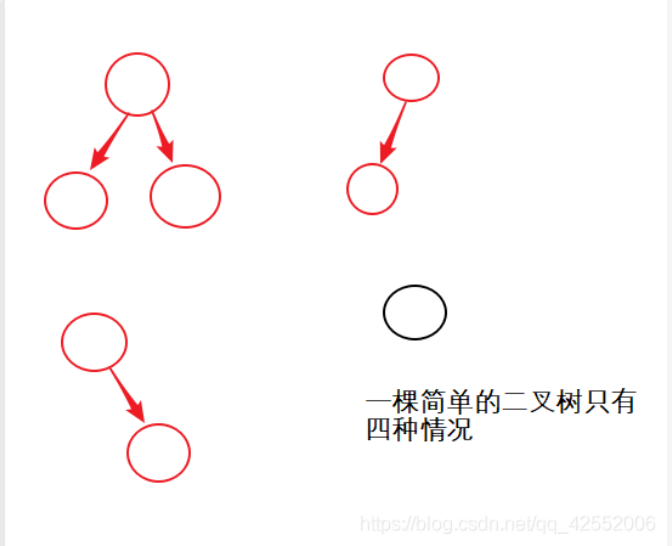
在这里插入图片描述以上就是二叉树的后序非递归的输出方法，下面的非递归的先序和中序不再进行一步一步的解释看代码中的注释就可以看懂

非递归的先序遍历二叉树

//非递归算法的先序遍历
void XXprint(Tree *tree){
    Stack s = initStack();   //初始化一个下面使用的栈
    treeNode *p = tree;    //新建一个遍历指针 
    while(p||!isEmpty(s)){
        while(p){
            cout<<p->data<<endl;
            push(s,p);
            p=p->lchild;
        }
        if(!isEmpty(s)){
            p = pop(s);
            p = p->rchild;
        }
    }
}

非递归的中序遍历二叉树

//非递归算法的中序遍历
void ZXprint(Tree *tree){
    Stack s = initStack();   //初始化一个下面使用的栈
    treeNode *p = tree;    //新建一个遍历指针 
    while(p||!isEmpty(s)){
        while(p){
            push(s,p);
            p=p->lchild;
        }
        if(!isEmpty(s)){
            p = pop(s);
            cout<<p->data<<endl;
            p=p->rchild;
        }
    }
}

层次遍历二叉树

//层次遍历二叉树
void levelprint(Tree *tree){
    queue<treeNode*> q;   //使用c++提供的类库进行队列的定义 
    q.push(tree);    //将根节点入队 
    while(!q.empty()){
        //当队不为空  循环 
        treeNode *p = q.front();   //获取队头结点 
        cout<<p->data<<endl;  //输出队头结点 
        q.pop();   //弹出队头 
        if(p->lchild!=NULL)    //如果队头有左孩子  左孩子入队    
        {
            q.push(p->lchild);
        }
        if(p->rchild!=NULL){
       //如果队头有右孩子  右孩子入队 
            q.push(p->rchild);
        }
    }
}

根节点入队进去while循环 p指向队头结点输出队头结点弹出队头
如果 p指向的结点有左孩子左孩子入队如果有右孩子右孩子入队
第二次进入while循环输出的即为根节点的左孩子结点此时p指向的左孩子结点没有左右孩子则结束本次循环
第三次进入循环输出的是根节点的右孩子结点这时 p指向的结点没有左孩子也没有右孩子结束总循环
这样输出的便是层次遍历的遍历结果

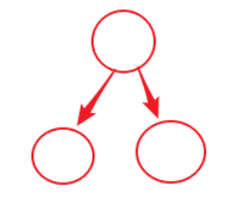
在这里插入图片描述

总代码

#include<iostream>
#include<stdlib.h>
#include <queue>
using namespace std;
typedef struct treeNode{
       //建立二叉树的存储结构 
    int data;
    treeNode *lchild,*rchild;
} Tree;
typedef struct SNode{
    treeNode *data[100];
    int top;
}SNode , *Stack;    //非递归遍历中使用的栈的存储结构 
//栈的初始化
Stack initStack(){
    Stack stack = (Stack)malloc(sizeof(SNode));   //使用c语言中的malloc函数分配空间  也可以使用new的方式 
    stack->top = -1;   //初始化栈顶指针 
    return stack;
}
//判断栈非空
bool isEmpty(Stack s){
       //栈的相关方法的重写 
    if(s->top == -1){
        return true;
    }else{
        return false;
    }
} 
//入栈
void push(Stack &s , treeNode *node)   //将一个树结点入栈 
{
    s->top++; 
    s->data[s->top] = node;
}
//出栈 
treeNode *pop(Stack &s)   //出栈的同时返回出栈的结点 
{
    if(s->top == -1){
        return false;
    }
    treeNode *temp = s->data[s->top];
    s->top--;
    return temp;
}
//获取栈顶结点
treeNode *getTop(Stack &s){
    if(s->top!=-1){
        treeNode *node = s->data[s->top];   //获取栈顶部的结点  但是不出栈 
        return node;
    }
}
//二叉树初始化方法
Tree *initTree(treeNode *root,int data){
    root->lchild = NULL;   //初始化根节点的左右孩子指针域 
    root->rchild = NULL;
    root->data = data;   //根节点赋值 
    return root;   
}
//插入一个左孩子结点
bool insertlchild(Tree *tree,int data){
    treeNode *l = (treeNode*)malloc(sizeof(treeNode));
    l->data = data;
    l->lchild = NULL;
    l->rchild = NULL;
    tree->lchild = l;
    return true;
} 
//插入一个右孩子结点
bool insertrchild(Tree *tree,int data){
    treeNode *r = new treeNode;
    r->data = data;
    r->rchild = NULL;
    r->lchild = NULL;
    tree->rchild = r;
} 
//递归遍历输出二叉树
void print (Tree *tree){
    if(tree)
    {
    print(tree->lchild);
    cout << tree->data<<endl;
    print(tree->rchild);
    }
} 
//非递归的后续遍历二叉树  
void HXprint(Tree *tree){
    Stack s = initStack();   //初始化一个下面使用的栈 
    treeNode *p = tree;    //新建一个遍历指针 
    treeNode *r=NULL;    //辅助变量 
    cout<<"-------"<<endl;
    while(p||!isEmpty(s)){
        //当遍历变量和栈同时为空时  表示遍历完成 
        if(p){
       //p非空  就入栈  并且遍历指针更改为指向当前节点的左孩子 
            push(s,p);
            p = p->lchild;
        }else{
        //p为空  表示当前节点已经没有左孩子 
            p = getTop(s);   //获取栈顶元素   也就是最后一个入栈的结点 
            if(p->rchild && p->rchild!=r){
       //判断栈顶结点是否有右孩子  
                p=p->rchild;    //修改指针一直找右孩子  直到没有右孩子  或者 右孩子已经访问过 
            }else{
                p = pop(s);  //如果没有右孩子  或者  右孩子已经访问过了 就开始出栈栈顶元素 
                cout<<p->data<<endl;    //输出当前指针指向的结点 
                r=p;      //将r修改为已经访问过的右孩子   防止再次访问到右孩子 
                p=NULL;   //将p修改为空指针 防止再次入栈 
            }
        }
    }
} 
//非递归算法的先序遍历
void XXprint(Tree *tree){
    Stack s = initStack();   //初始化一个下面使用的栈
    treeNode *p = tree;    //新建一个遍历指针 
    while(p||!isEmpty(s)){
        while(p){
            cout<<p->data<<endl;
            push(s,p);
            p=p->lchild;
        }
        if(!isEmpty(s)){
            p = pop(s);
            p = p->rchild;
        }
    }
} 
//非递归算法的中序遍历
void ZXprint(Tree *tree){
    Stack s = initStack();   //初始化一个下面使用的栈
    treeNode *p = tree;    //新建一个遍历指针 
    while(p||!isEmpty(s)){
        while(p){
            push(s,p);
            p=p->lchild;
        }
        if(!isEmpty(s)){
            p = pop(s);
            cout<<p->data<<endl;
            p=p->rchild;
        }
    }
}
//层次遍历二叉树
void levelprint(Tree *tree){
    queue<treeNode*> q;   //使用c++提供的类库进行队列的定义 
    q.push(tree);    //将根节点入队 
    while(!q.empty()){
        //当队不为空  循环 
        treeNode *p = q.front();   //获取队头结点 
        cout<<p->data<<endl;  //输出队头结点 
        q.pop();   //弹出队头 
        if(p->lchild!=NULL)    //如果队头有左孩子  左孩子入队    
        {
            q.push(p->lchild);
        }
        if(p->rchild!=NULL){
       //如果队头有右孩子  右孩子入队 
            q.push(p->rchild);
        }
    }
}
int main ()
{
    Tree *T = new Tree;
    initTree(T,1);
    insertlchild(T,2);
    insertrchild(T,3);
    insertlchild(T->lchild,4);
    insertrchild(T->lchild,5);
    insertlchild(T->rchild,6);
    insertrchild(T->rchild,7);
    cout<<"递归中序遍历二叉树"<<endl;
    print (T);
    cout<<"非递归后序遍历二叉树"<<endl;
    HXprint(T);
    cout<<"非递归先序遍历二叉树"<<endl;
    XXprint(T);
    cout<<"非递归中序遍历二叉树"<<endl;
    ZXprint(T);
    cout<<"层次遍历二叉树"<<endl;
    levelprint(T);
    return 0;
}