【递归】 LeetCode51. N皇后-蒲公英云

【递归】 LeetCode51. N皇后

题目

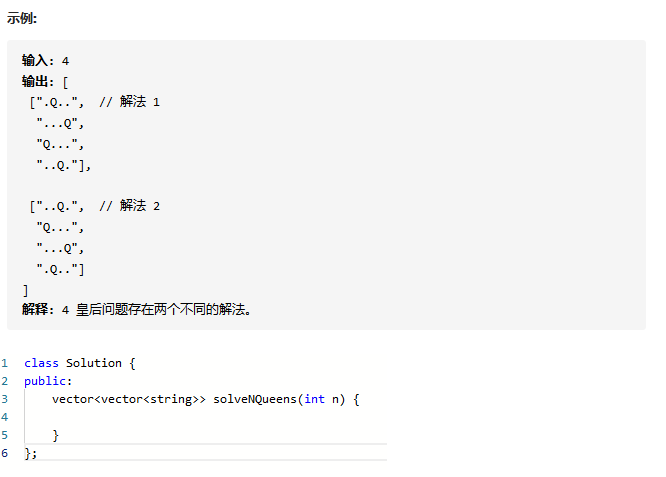
在这里插入图片描述

解答

回溯法的求解过程实质上是一个先序遍历一棵状态树的过程，只是这棵树不是遍历前预先建立的，而是隐含在遍历的过程中。

递归题的解法：首先把题目的决策树画出来，树的层就是for循环，树的深度就是要递归的参数i。画出决策树后，找规律，进行剪枝。

皇后横竖斜方向的棋子都会被吃掉，棋盘每行只能放一个皇后。

E.g. 输入 n = 4

树的层为棋子放入棋盘哪一列，树的深度为放入棋盘哪一行。
在这里插入图片描述

代码

#include <iostream>
#include <string>
#include <list>
#include <vector>
#include <map>
#include <utility>
#include <functional>
#include <algorithm>
#include <cassert>
// 51. N-Queens
// 使用std::vector<std::vector<int>> chessboard来标记棋盘所有被攻击的位置为1，没有被攻击的位置为0。
// 将皇后放到(x,y)并且标记其所有的攻击位置。
void MarkAttackPosition(int x, int y, std::vector<std::vector<int>>& chessboard) { 
  // (x,y)这个点上下左右斜对角九个点，相对于x的偏移量。（X,Y）= N(dx,dy) + (x,y)
  static const int N = 9;
  static const int dx[N] = {  -1, -1, -1, 0, 0, 0, 1, 1, 1 };
  static const int dy[N] = {  -1, 0, 1, -1, 0, 1, -1, 0, 1};
  const int kChessboardLen = chessboard.size();
  for (int i = 0; i < kChessboardLen; i++) { 
    for (int j = 0; j < N; j++) { 
      int temp_x = x + i * dx[j];
      int temp_y = y + i * dy[j];
      if (temp_x < 0 || temp_y < 0 || temp_x >= kChessboardLen || temp_y >= kChessboardLen) { 
        continue;
      }
      chessboard[temp_x][temp_y] = 1;
    }
  }
}
// 回溯法的求解过程实质上是一个先序遍历一棵状态树的过程，只是这棵树不是遍历前预先建立的，而是隐含在遍历的过程中。
// 所以解答此类题的关键就是找到这棵树，然后将题目转化为遍历树的过程。
// i 代表行，j代表列。一行一行的去放值，首先放置在第一行，然后依次尝试放在每一列，尝试一个可行列后继续放下一行。可以展开成一棵树。
void PlaceQueen(int i, int n,
                std::vector<std::vector<int>>& chessboard,
                std::vector<std::string>& subset,
                std::vector<std::vector<std::string>>& subsets) { 
  if (i >= n) { 
    subsets.push_back(subset);
    return;
  }
  for (int j = 0; j < n; ++j) { 
    if (chessboard[i][j] == 1) { 
      continue;
    }
    std::vector<std::vector<int>> backup_chessboard = chessboard;
    // 尝试放在(i, j)。
    MarkAttackPosition(i, j, chessboard);
    subset[i][j] = 'Q';
    PlaceQueen(i + 1, n, chessboard, subset, subsets);
    // 接下来将尝试放在(i, j+1)这个位置，所以要恢复到之前的状态。
    subset[i][j] = '.';
    chessboard = backup_chessboard;
  }
}
std::vector<std::vector<std::string>> solveNQueens(int n) { 
  std::vector<std::vector<std::string>> subsets;
  std::vector<std::string> subset(n, std::string(n, '.'));
  std::vector<std::vector<int>> chessboard(n, std::vector<int>(n, 0));
  PlaceQueen(0, n, chessboard, subset, subsets);
  return subsets;
}
void PrintChessboard(const std::vector<std::vector<int>>& chessboard) { 
  for (const auto& line : chessboard) { 
    for (auto i : line) { 
      std::cout << i;
    }
    std::cout << std::endl;
  }
}
void PrintSubsets(const std::vector<std::vector<std::string>>& subsets) { 
  for (const auto& subset : subsets) { 
    for (const auto& line : subset) { 
      std::cout << line << std::endl;
    }
    std::cout << "------------------------" << std::endl;
  }
}
int main() { 
  PrintSubsets(solveNQueens(8));
  return 0;
}