Leetcode84 柱状图中最大的矩形详细的解法-蒲公英云

Leetcode84 柱状图中最大的矩形详细的解法

红太狼 2022-10-09 00:55 216阅读 0赞

求在该柱状图中，能够勾勒出来的矩形的最大面积。

以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

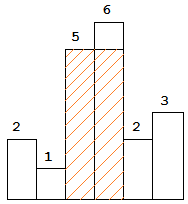
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10
1
2
解题思路

这个问题非常有意思。我们首先可以想到的是暴力破解，我们通过i不断遍历heights，然后在遍历的过程中通过j不断向后寻找最大矩形。

例如，我们把i从1开始遍历，j在[i,len(heights)]区间遍历。

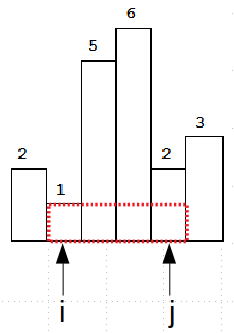
接着我们i从2开始遍历，j在[i,len(heights)]区间遍历。

class Solution:
def largestRectangleArea(self, heights):
“””
:type heights: List[int]
int
“””
if not heights:
return 0
heights_len = len(heights)
res = 0
i, j = 0, 0
while i < heights_len:
min_h = heights[i]
for j in range(i, heights_len):
min_h = min(min_h, heights[j])
res = max(res, min_h*(j - i + 1))
i += 1

    return res

这种解法显然很慢，我们有一种更好的思路就是通过递增栈。所谓的递增栈，就是栈中只存放递增序列。

我们首先将2加入到栈中，我们接着访问1，我们发现1比栈顶元素2小，所以我们将栈顶元素2弹出，并且记录此时的面积2。我们发现栈已经空了，所以我们要接着压栈。

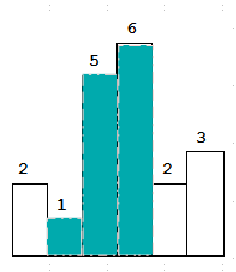
接着我们通过不断遍历找到第二个递增栈。

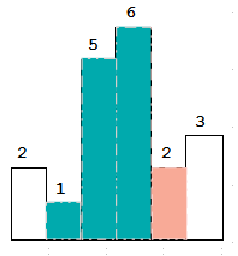
我们接着访问2，我们发现此时2比栈顶元素6小，所以我们弹出栈顶元素6，并且记录此时的面积6*1=6。

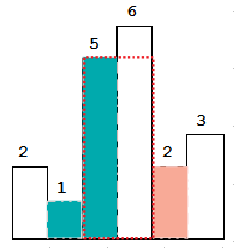
此时栈中还有元素，我们发现此时2依旧比栈顶元素5小，所以我们需要将栈顶元素5弹出，并且我们记录此时出栈元素构成的最大面积5*2=10。

我们发现此时的2比栈顶元素大了，我们就将2压入栈中，接着将3压入栈中。此时遍历结束，我们发现栈不为空，所以我们需要进行出栈操作，出栈的同时记录出栈元素构成的最大面积即可。

class Solution:
def largestRectangleArea(self, heights):
“””
:type heights: List[int]
int
“””
stack = list()
res, i = 0, 0
while i < len(heights):
if not stack or (heights[i] >= heights[stack[-1]]):
stack.append(i)
i += 1
else:
k = stack.pop()
res = max(res, heights[k]*((i - stack[-1] - 1) if stack else i))

    while stack:  
        k = stack.pop()  
        res = max(res, heights\[k\]\*((i - stack\[-1\] - 1) if stack else i))  
    return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
一个更简洁的写法。

class Solution:
def largestRectangleArea(self, heights):
“””
:type heights: List[int]
int
“””
stack = [-1]
res = 0
heights.append(-1)

    for idx, val in enumerate(heights):  
        while heights\[stack\[-1\]\] > val:  
            h = heights\[stack.pop()\]  
            res = max(res, h\*(idx - stack\[-1\] -1))
        stack.append(idx)
    return res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
我将该问题的其他语言版本添加到了我的GitHub Leetcode

如有问题，希望大家指出！！！
————————————————
版权声明：本文为CSDN博主「coordinate_blog」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq\_17550379/article/details/85093224