【数据结构练习习题】java实现版（一）

男娘i 2022-10-07 06:55 308阅读 0赞

### 练习目录 ###

*  仅用递归函数和栈操作逆序一个栈 不能用其他数据结构
 *  一个栈中元素的类型为整型，现在想将该栈从顶到底按从大到小的顺序排序，只许申请一个栈。
 *  数组
 *   *  在o(N)时间复杂度内查找数组中前三名
     *  一个数组中求三个数使得三个数乘积最大
     *  求一个无序数组中的两个数，之和为给定的target
     *  更改上面的题目条件：改为升序数组
     *  旋转z数组的最小元素
     *  删除排序数组的重复元素
     *  寻找数组中心下标
     *  生成窗口最大值数组
 *  树
 *   *  把一个有序的整数数组放到二叉树中
     *  求最大子树和
     *  输入一棵二元查找树，将该二元查找树转换成一个排序的双向链表。
     *  输入一个整数数组，判断该数组是否是某二元查找树的后序遍历的结果
 *  求x的平方根整数部分
 *  斐波那契数列的三种解法
 *  排列硬币

--------------------

# 仅用递归函数和栈操作逆序一个栈 不能用其他数据结构 #

思路：设计两个递归函数，其中一个用于得到栈底的元素，另一个用于依次逆序栈，最后可得到一个新栈

//先设计一个递归函数将栈的栈底元素返回并移除
    
      public static int getAndRemoveLast(Stack<Integer>stack)
        { 
            int result = stack.pop();
            if(stack.empty()) return result;
            else
            { 
                int last=getAndRemoveLast(stack);
                stack.push(result);
                return last;
            }
        }
        //递归函数2
        public static void reverse(Stack<Integer>stack)
        { 
            if(stack.empty())return;
            else{ 
                int i = getAndRemoveLast(stack);
                reverse(stack);
                stack.push(i);
            }
        }

函数一过程：  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzU4NTc0_size_16_color_FFFFFF_t_70]

注意递归函数中递归和push的顺序，函数二先调用取栈底的函数，再调用自身  
函数二过程：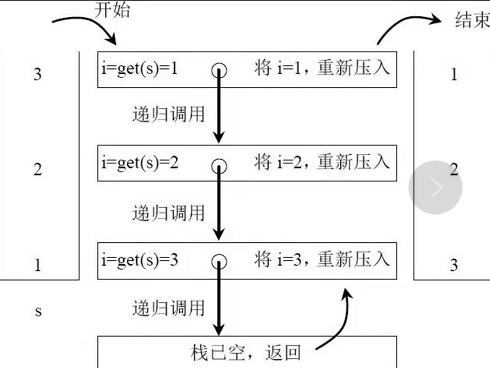  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzU4NTc0_size_16_color_FFFFFF_t_70 1]

# 一个栈中元素的类型为整型，现在想将该栈从顶到底按从大到小的顺序排序，只许申请一个栈。 #

除此之外，可以申请新的变量，但不能申请额外的数据结构。如何完成排序？  
【难度】 士　★☆☆☆  
【解答】 将要排序的栈记为stack，申请的辅助栈记为help。在stack上执行pop操作，弹出的元素记为cur。 如果cur小于或等于help的栈顶元素，则将cur直接压入help；如果cur大于help的栈顶元素，则将help的元素逐一弹出，逐一压入stack，直到cur小于或等于help的栈顶元素，再将cur压入help。 一直执行以上操作，直到stack中的全部元素都压入到help。最后将help中的所有元素逐一压入stack，即完成排序。

（自己写的）：

Stack<Integer>help=new Stack<Integer>();
            while(!stack.empty())
            { 
              if(help.empty())
                    help.push(a);
                else if(help.peek()>=a)help.push(a);
                else { 
                    while(!help.empty())
                    { 
                        int b=help.pop();
                        stack.push(b);
                        if(b >=a ||help.empty()) { 
                            help.push(a);
                            break;
                        }
                    }
                }

题解的：（简洁很多）

public static void sortStack(Stack<Integer>stack)
        { 
            Stack<Integer>help=new Stack<Integer>();
            while(!stack.empty())
            { 
                int a =stack.pop();
                while(!help.empty() && help.peek()<a)
                    stack.push(help.pop());
                help.push(a);//其他情况都推入help
                while(!help.empty())
                    stack.push(help.pop());//最后把help的元素都推入原stack
               
                }
            
        }

# 数组 #

## 在o(N)时间复杂度内查找数组中前三名 ##

如果没有时间复杂度的要求，可以首先对整个数组进行排序，然后根据数组下标就可以非常容易地找出最大的三个数，即前三名。由于这种方法的效率高低取决于排序算法的效率高低，因此，这种方法在最好的情况下时间复杂度都为O（NlogN）。 通过分析发现，最大的三个数比数组中其他的数都大。因此，可以采用类似求最大值的方法来求前三名。具体实现思路：初始化前三名（r1：第一名，r2：第二名，r3：第三名）为最小的整数。然后开始遍历数组：  
1）如果当前值tmp大于r1：r3=r2，r2=r1，r1=tmp;  
2）如果当前值tmp大于r2且不等于r1：r3=r2，r2=tmp；  
3）如果当前值tmp大于r3且不等于r2：r3=tmp。

public class findTop3 { 
        //最大的前三个数
        public static void Test(int arr[]){ 
            int r1,r2,r3,temp;
            r1 = r2 = r3 = Integer.MIN_VALUE;
            if(arr == null || arr.length < 3){ 
                System.out.println("参数不合法");
                return;
            }
            for(int i = 0;i < arr.length;i++){ 
                if(arr[i] > r1) { 
                  r3 = r2;//如果arr[i]比最大的更大，则更新，将上一个最大的赋给次大的
                  r2 = r1;
    
                    r1 = arr[i];
                }
                else if(arr[i] > r2 && arr[i] != r1)
                { 
                    r3 = r2;
                    r2 = arr[i];
                }
                else if(arr[i] > r3 && arr[i] != r2)
                { 
                    r3 = arr[i];
                }
            }
            System.out.println("前三名："+r1+" "+r2+" "+r3);
        }
    
        public static void main(String[] args) { 
            int arr[] = { 4,7,9,2,3,0};
            Test(arr);
        }
    }

## 一个数组中求三个数使得三个数乘积最大 ##

public static int sort(int[]nums)
    { 
      int min1 = Integer.MAX_VALUE,min2 = Integer.MAX_VALUE;
      int max1 = Integer.MIN_VALUE;
      int max2 = max1,max3 = max1;
    
    for(int x:nums){ 
        if(x < min1)
        { //如果x比最小的还小
            min2 = min1;
            min1 = x;//原来最小的变成第二小的，x变成最小的
        }
        else if(x < min2)
            min2 = x;
        if(x > max1)
        { 
            max3 = max2;
            max2 = max1;
            max1 = x;
    
    
        }else if(x > max2)
        { 
            max3 = max2;
            max2 = x;
        }
        else if(x > max3)
            max3 = x;
        System.out.println(min1+","+min2+","+max1+" "+max2+" "+max3);
    }
    return Math.max(min1*min2*max1,max1*max2*max3);//考虑有正数也有负数，如果是两个最小的负数和一正数乘积可能比三个正数大
        //其余情况都是三个最大值乘积最大
    }
        public static void main(String[] args) { 
            int []nums = { -10,-2,-3,-10,-5,9,5};
            System.out.println(sort(nums));
        }

## 求一个无序数组中的两个数，之和为给定的target ##

返回一个数组，数组中存放两数的下标  
给定初始数组和target整数，从数组中找出两个数满足相加之和为target 假定每个输入只对应唯一的答案，且不重复使用相同的元素  
常规：暴力法，双重for循环，时间复杂度高  
优化法：用一个map存储下标和对应的元素，时间复杂度变为o(N)

public static int[]solution(int[]nums,int target)
    { 
        public static int[]solution(int[]nums,int target)
        { 
    Map<Integer,Integer>map = new HashMap<>();
    for(int i = 0;i < nums.length;i++)
    { 
        if(map.containsKey(target - nums[i]))
            return new int[]{ map.get(target - nums[i]),i};
    
            map.put(nums[i],i);
    }
    return new int[0];
        }
        public static void main(String[] args) { 
            int []nums = { -10,-2,-3,-10,-5,9,5,3};
            int [] a = solution(nums,0);
            for(int i:a)
            System.out.println(i);
        }
    }

## 更改上面的题目条件：改为升序数组 ##

其他条件不变，找和为目标的两数下标  
方法一：二分法

public static int[] binary(int[]nums,int target) { 
            for (int i = 0; i < nums.length; i++) { 
                int low = i;
                int high = nums.length - 1;
                while (low <= high) { 
                    int mid = (high - low) / 2 + low;
                    if (nums[mid] == target - nums[i]) return new int[]{ i, mid};
                    else if (nums[mid] > target - nums[i]) { 
                        high = mid - 1;
                    } else
                        low = mid + 1;
                }
            }
            return new int[0];
        }

法2 双指针法(时间复杂度更优）是最优解

public static int[] towpoints(int[] nums,int target)
        { 
            int low = 0,high = nums.length - 1;
            while(low < high)
            { 
                int sum = nums[low] + nums[high];
                if(sum == target) return new int[]{ low,high};
                else if(sum < target) low++;
                else high--;
            }
            return new int[0];
        }

时间复杂度为o(n)

## 旋转z数组的最小元素 ##

把一个有序数组最开始的若干个元素搬到数组  
的末尾，称之为数组的旋转。输入一个排好序的数组的一个旋转，输出旋转数组的最小元素。例如，数组\{3, 4, 5, 1, 2\}为数组\{1, 2, 3, 4, 5\}的一个旋转，该数组的最小值为1。 分析与解答： 其实这是一个非常基本和常用的数组操作，它的描述如下： 有一个数组X\[0…n-1\]，现在把它分为两个子数组：x1\[0…m\]和x2\[m+1…n-1\]，交换这两个子数组，使数组x由x1x2变成x2x1，例如x=\{1，2，3，4，5，6，7，8，9\}，x1=\{1，2，3， 4，5\}，x2=\{6，7，8，9\}，交换后，x=\{6，7，8，9，1，2，3，4，5\}。 对于本题的解决方案，最容易想到的，也是最简单的方法就是直接遍历法。但是这种方法显然没有用到题目中旋转数组的特性，因此，它的效率比较低。下面介绍一种比较高效的二分查找法。 通过数组的特性可以发现，数组元素首先是递增的，然后突然下降到最小值，然后再递增。虽然如此，但是还有下面三种特殊情况需要注意：  
1）数组本身是没有发生过旋转的，是一个有序的数组，如序列\{1,2,3,4,5,6\}。  
2）数组中元素值全部相等，如序列\{1,1,1,1,1,1\}。  
3）数组中元素值大部分都相等，如序列\{1,0,1,1,1,1\}。  
通过旋转数组的定义可知，经过旋转之后的数组实际上可以划分为两个有序的子数组，前面的子数组的元素值都大于或者等于后面子数组的元素值。可以根据数组元素的这个特点，采用二分查找的思想不断缩小查找范围，最终找出问题的解决方案。 按照二分查找的思想，给定数组arr，首先定义两个变量low和high，分别表示数组的第一个元素和最后一个元素的下标。按照题目中对旋转规则的定义，第一个元素应该是大于或者等于最后一个元素的（当旋转个数为0，即没有旋转时，要单独处理，直接返回数组第一个元素）。接着遍历数组中间的元素arr\[mid\]，其中mid=（high+low）/2。  
1）如果arr\[mid\]＜arr\[mid-1\]，则arr\[mid\]一定是最小值；  
2）如果arr\[mid+1\]＜arr\[mid\]，则arr\[mid+1\]一定是最小值；  
3）如果arr\[high\]＞arr\[mid\]，则最小值一定在数组左半部分；  
4）如果arr\[mid\]＞arr\[low\]，则最小值一定在数组右半部分；

5）如果arr\[low\]==arr\[mid\] 且 arr\[high\]==arr\[mid\]，则此时无法区分最小值是在数组的左半部分还是右半部分（例如，\{2,2,2,2,1,2\}，\{2,1,2,2,2,2,2\}）。在这种情况下，只能分别在数组的左右两部分找最小值minL与minR，最后求出minL与minR的最小值。

public class findMin { 
        
      public static int getMin(int[]arr,int low,int high){ 
          if(low > high) return arr[0];//如果选择个数为0，即没有旋转，单独处理，返回头元素
          if(low == high) return arr[low];
          int mid = low+((high - low) >>1);//这样运算防止溢出
          if(arr[mid-1] >arr[mid])return arr[mid];
          else if(arr[mid] > arr[mid+1]) return arr[mid+1];
          else if(arr[mid] <arr[high] ) return getMin(arr,low,mid-1);
         else if(arr[mid]>arr[low]) return getMin(arr,mid+1,high);
          else return Math.min(getMin(arr,low,mid-1),getMin(arr,mid+1,high));//arr[low]==arr[mid] 且 arr[high]==arr[mid]
      }
      public static int getMin(int[]arr){ 
          if(arr == null){ 
              System.out.println("参数不合法！");
              return -1;
          }
          return getMin(arr,0,arr.length-1);
      }
    
        public static void main(String[] args) { 
            int arr[] = { 2,2,2,2,2,1,2};
          int mii =   getMin(arr);
            System.out.println(mii);
    
        }
    }

一般而言，二分查找的时间复杂度为O（logN），对于这道题而言，大部分情况下时间复杂度为O（logN），只有每次都满足上述条件5）的时候才需要对数组中所有元素都进行遍历，因此，这种方法在最坏的情况下的时间复杂度为O（N）。  
难点：考虑到不同的多种情况  
考虑特殊情况  
在不同情况下递归时的参数是多少（最小值到底是在左半部分还是右半部分容易弄错，可以自己模拟一个数组判断

## 删除排序数组的重复元素 ##

一个有序数组，删除重复出现的元素，使得每个元素只出现一次，返回删除后数组的新长度，不能使用额外的空间，必须在原地修改输入数组  
考察：双指针法  
用一个快慢指针（数组中的下标模拟指针），初始指针j在i的前面，当没有重复元素时i指针都递增，并且将nums\[i\]的元素变为nums\[j\]（如果有重复元素，j继续加一，i不变）最后i的位置即长度

public static int removeDupicates(int[]nums)
    { 
    if(nums.length == 0)
    return 0;
    int i = 0;
    for(int j = 1;j < nums.length;j++)
    { 
    if(nums[i]!=nums[j])
    { i++;
    nums[i] = nums[j];//注意这两句话执行顺序，且都是在if后面
    }
    }
    return i;
    }

## 寻找数组中心下标 ##

中心下标是一个下标值，它左边的所有元素相加之和等于右侧所有元素相加之和。如果不存在，返回-1，如果有多个，返回最左边的

public static int privotIndex(int[]nums)
    { 
    int sum = Arrays.stream(num).sum();
    int total = 0;
    for(int i = 0;i < nums.length;i++)
    { 
    total += nums[i];
    if(total == sum)
    return i;
    sum -= nums[i];//注意这个if和sum-=的顺序,是类似于total占领的元素与sum占领的元素相等时，二者重合的那个元素下标就是需要返回的下标
    
    }
    return -1;
    }

## 生成窗口最大值数组 ##

有一个整型数组arr和一个大小为w的窗口从数组的最左边滑到最右边，窗口每次向右边滑一个位置。 例如，数组为\[4，3，5，4，3，3，6，7\]，窗口大小为3时： \[4 3 5\] 4 3 3 6 7 窗口中最大值为5  
4 \[3 5 4\] 3 3 6 7 窗口中最大值为5  
4 3 \[5 4 3\] 3 6 7 窗口中最大值为5  
4 3 5 \[4 3 3\] 6 7 窗口中最大值为4  
4 3 5 4 \[3 3 6\] 7 窗口中最大值为6  
4 3 5 4 3 \[3 6 7\] 窗口中最大值为7  
如果数组长度为n，窗口大小为w，则一共产生n-w+1个窗口的最大值。 请实现一个函数。 输入：整型数组arr，窗口大小为w。 输出：一个长度为n-w+1的数组res，res\[i\]表示每一种窗口状态下的最大值。 以本题为例，结果应该返回\{5，5，5，4，6，7\}。  
【难度】 尉　★★☆☆  
【解答】 如果数组长度为N，窗口大小为w，如果做出时间复杂度O（N×w）的解法是不能让面试官满意的，本题要求面试者想出时间复杂度O（N）的实现。 本题的关键在于利用双端队列来实现窗口最大值的更新。首先生成双端队列qmax，qmax中存放数组arr中的下标。

一定要注意qmax中存放的是索引，如果在比较时要与arr\[qmax.peekfirst()\]比较

public static int[] getMaxWindow(int[]arr,int w){ 
            if(arr == null || w < 1||arr.length < w) return null;
                LinkedList<Integer> qmax = new LinkedList<>();
                int index = 0;
                int[]res = new int[arr.length - w + 1];
                for (int i = 0; i < arr.length; i++) { 
                    while (!qmax.isEmpty() && arr[i] > arr[qmax.peekFirst()])
                        qmax.pollLast();
                    qmax.addLast(i);
                    if(qmax.peekFirst() == i - w)//如果过期
                        qmax.pollFirst();
                    if(i >= w -1)//注意i是从0开始，i为0表示第一个元素
                        res[index++] = arr[qmax.peekFirst()];//注意qmax中存放的是索引而不是具体的元素值
                }
        return res;
        }
        public static void main(String[] args) { 
          int[]arr = getMaxWindow(new int[]{ 4,3,5,4,3,3,6,7},3);
            for (int i = 0; i < arr.length; i++) { 
                System.out.println(arr[i]);
            }

# 树 #

## 把一个有序的整数数组放到二叉树中 ##

//把一个有序的整数数组放到二叉树中  
//思路：取数组中间元素作为根节点，数组分为左右两部分，对两部分用递归的方法分别构建左右子树

public class Test { 
     
        public static void main(String[] args) { 
            int[]arr = { 4,7,8,9,11,16,18};
            Btnode btnode = new Btnode();
            btnode=Btnode.build(arr,0,arr.length-1);
            Btnode.Inorder(btnode);
            //中序遍历时二叉树打印的顺序即有序数组的顺序
        }
    }
    class Btnode{ 
        int data;
        Btnode lchild,rchild;
        public static Btnode build(int[]arr,int low,int high){ 
    
            Btnode node = null;
            if(low <= high) { 
                node = new Btnode();
                int mid = (low+high)/2;
                node.data = arr[mid];
                node.lchild = build(arr, low, mid - 1);
                node.rchild = build(arr, mid + 1, high);
            }
            else { 
                node = null
                        ;
            }
            return node;
        }
        public static void Inorder(Btnode node){ 
            if(node == null) return;
            else { 
                if (node.lchild != null)
                { 
                    Inorder(node.lchild);
                }
                System.out.println(node.data+"->");
                if (node.rchild != null)
                { 
                    Inorder(node.rchild);
                }
            }
        }
    }

## 求最大子树和 ##

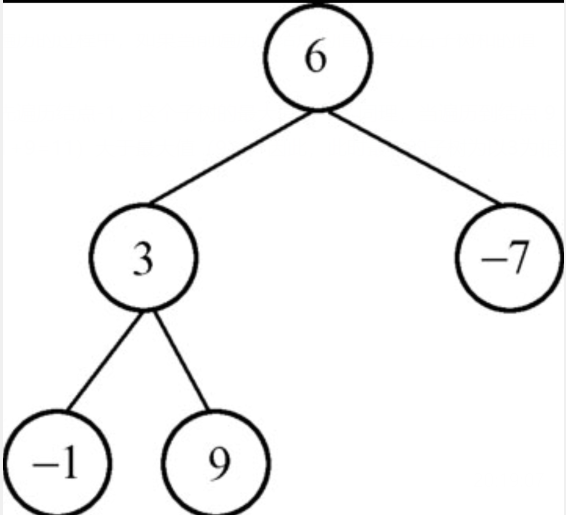
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzU4NTc0_size_16_color_FFFFFF_t_70 2]

在上图中，首先遍历结点-1，这个子树的最大值为-1。同理，当遍历到结点 9 时，子树的最大值为9，当遍历到结点3时，这个结点与其左右孩子结点值的和（3-1+9=11）大于最大值（9）。因此，此时最大的子树为以3为根结点的子树，依此类推，直到遍历完整棵树为止。实现代码如下：

class Btnode{ 
        int data;
        Btnode lchild,rchild;
      
        private static int maxSum = Integer.MIN_VALUE;
        /* 求最大子树 */
        public static int findMaxSubTree(Btnode root,Btnode maxRoot)
        { 
            if(root == null) return 0;
            int lmax = findMaxSubTree(root.lchild,maxRoot);
            int rmax = findMaxSubTree(root.rchild,maxRoot);
            int sum = rmax + lmax + root.data;
            if(sum > maxSum)
            { 
                maxSum = sum;
                maxRoot.data = root.data;//用于确定取得最大子树的根节点编号
    
            }
            return sum;//返回以root为结点的子树和
    
        }
    public static Btnode buildTree()
    { 
        Btnode root = new Btnode();
        Btnode node1 = new Btnode();
        Btnode node2 = new Btnode();
        Btnode node3 = new Btnode();
        Btnode node4 = new Btnode();
        root.data = 6;
        node1.data = 3;
        node2.data = -7;
        node3.data = -1;
        node4.data = 9;
        root.lchild = node1;
        root.rchild = node2;
        node1.lchild = node3;
        node1.rchild = node4;
        node2.lchild = node2.rchild = node3.rchild = node3.lchild = node4.rchild = node4.lchild = null;
        return root;
    }
        public static void main(String[] args) { 
            Btnode btnode = new Btnode();
            Btnode maxNode = new Btnode();
            btnode = Btnode.buildTree();
            Btnode.findMaxSubTree(btnode,maxNode);
            System.out.println("最大子树和"+maxSum);
            System.out.println("树的根节点："+maxNode.data);
    
        }
    }

![在这里插入图片描述][20210713022430542.png]

## 输入一棵二元查找树，将该二元查找树转换成一个排序的双向链表。 ##

要求不能创建任何新的结点，只能调整结点的指向，例如下图。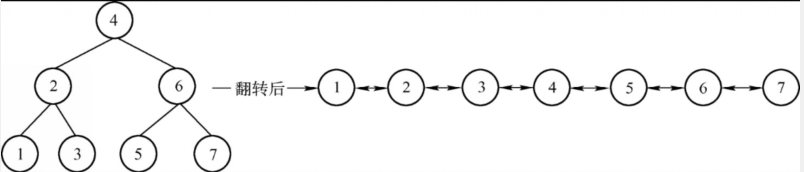  
![在这里插入图片描述][20210713023332143.png]  
由于转换后的双向链表中结点的顺序与二叉树的中序遍历的顺序相同，因此，可以对二叉树的中序遍历算法进行修改。通过在中序遍历的过程中修改结点的指向来转换成一个排序的双向链表。实现思路如下图所示：假设当前遍历的结点为root，root的左子树已经被转换为双向链表，如下图（1）所示。使用两个变量pHead与pEnd分别指向链表的头结点与尾结点。那么在遍历root结点时，**只需要将root结点的lchild指向pEnd，把pEnd的rchild（右）指向root；此时root结点就被加入到双向链表里了**。因此，root变成了双向链表的尾结点。对于所有的结点都可以通过同样的方法来修改结点的指向。因此，可以采用递归的方法来求解，在求解时需要特别注意递归的结束条件和边界情况（例如双向链表为空的时候）。

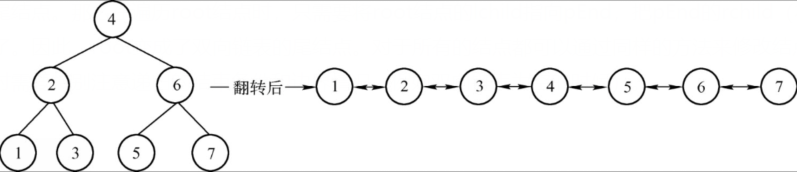
![在这里插入图片描述][20210713023438746.png]

class Btnode{ 
        int data;
        Btnode lchild,rchild;
        public static Btnode build(int[]arr,int low,int high){ 
    
            Btnode node = null;
            if(low <= high) { 
                node = new Btnode();
                int mid = (low+high)/2;
                node.data = arr[mid];
                node.lchild = build(arr, low, mid - 1);
                node.rchild = build(arr, mid + 1, high);
            }
            else { 
                node = null
                        ;
            }
            return node;
        }
        public static void Inorder(Btnode node){ 
            if(node == null) return;
            else { 
                if (node.lchild != null)
                { 
                    Inorder(node.lchild);
                }
                System.out.println(node.data+"->");
                if (node.rchild != null)
                { 
                    Inorder(node.rchild);
                }
            }
        }
    
        private static int maxSum = Integer.MIN_VALUE;
     private static Btnode pHead = null;
     private static Btnode pEnd = null;//链表首尾结点
        /* 参数：二叉树根结点 */
        public static void inOrderBSTress(Btnode root)
        { 
            if(root == null) return;
            if(root.lchild !=null) inOrderBSTress(root.lchild);
            root.lchild = pEnd;
            if(pEnd == null)
            { 
                pHead = root;//如果当前链表为空，当前遍历的结点作为双向链表头结点
            }
            else
            { 
                pEnd.rchild = root;
    
            }
            pEnd = root;//root成为新的尾结点 写在if的外面，表示不论是否双向链表为空，都执行此操作 联想尾插法
            if(root.rchild !=null) inOrderBSTress(root.rchild);
    
        }
    
    
    
        public static void main(String[] args) { 
    
            int arr[] = { 1, 2, 3, 4, 5, 6, 7};
            Btnode btnode = build(arr, 0, arr.length - 1);//将数组放入树中形成一个查找树
            inOrderBSTress(btnode);
            Btnode cur;
            System.out.println("转换后双向链表：");
            for (cur = pHead; cur != null; cur = cur.rchild)
            { 
                System.out.print(cur.data+",");
            }
    
    
        }
    }

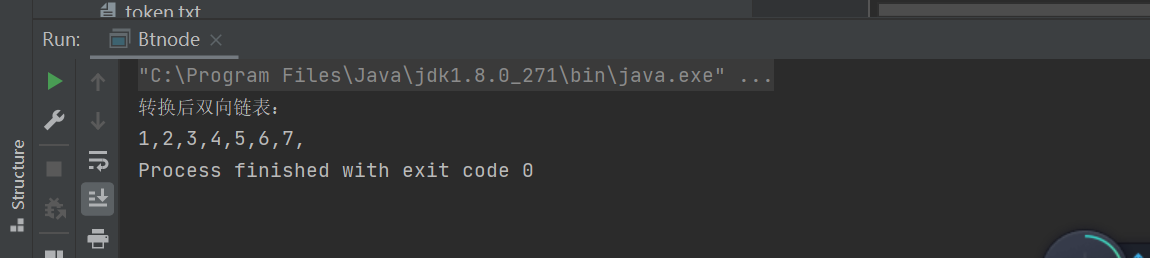
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzU4NTc0_size_16_color_FFFFFF_t_70 3]  
时间复杂度o(n) 只用了两个额外变量pHead pEnd来记录双向链表首尾结点，空间复杂度o(1)

## 输入一个整数数组，判断该数组是否是某二元查找树的后序遍历的结果 ##

如果是，那么返回true，否则返回false。例如，数组\{1,3,2,5,7,6,4\}就是下图中二叉树的后序遍历序列。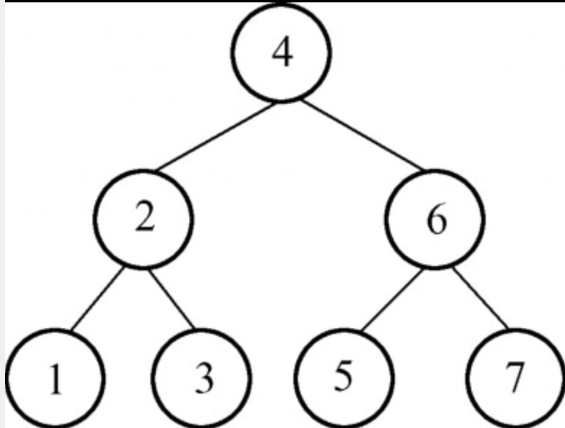  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzU4NTc0_size_16_color_FFFFFF_t_70 4]

二元查找树的特点：对于任意一个结点，它的左子树上所有结点的值都小于这个结点的值，它的右子树上所有结点的值都大于这个结点的值。根据这个特点及二元查找树后序遍历的特点可以看出，这个序列的最后一个元素一定是树的根结点（上图中的结点4），然后在数组中找到第一个大于根结点4的值5，那么结点5之前的序列（1,3,2）对应的结点一定位于结点4的左子树上，结点5（包含这个结点）后面的序列一定位于结点4的右子树上（也就是说，结点5后面的所有值都应该大于或等于4）。对于结点4的左子树遍历的序列\{1,3,2\}，以及右子树的遍历序列\{5,7,6\}可以采用同样的方法来分析，因此，可以通过递归方法来实现。

public static boolean IsAfterOrder(int[]arr,int start,int end)
    { 
        if(arr == null) return false;
        int root = arr[end];
        int i,j;
        for(i = start;i < end;i++)
            if(arr[i] > root)
                break;
        for(j = i;j < end;j++)
            if(arr[j] < root)
                return false;
            boolean isLeft  = true;
            boolean isRight = true;
            if(i > start)//判断小于Root的序列是否为查找树的后序遍历
            isLeft = IsAfterOrder(arr,start,i-1);
            if(j < end)//判断大于Root的序列是否为查找树的后序遍历
            isRight = IsAfterOrder(arr,i,end);
            return isLeft && isRight;
    }
        public static void main(String[] args) { 
    
    
           int arr[] = { 1,3,2,5,7,6,4};
           boolean reasult = IsAfterOrder(arr,0,arr.length-1);
           if(reasult == true) System.out.println("是");
           else System.out.println("不是");
           }
           }

输出“是”

# 求x的平方根整数部分 #

考察：二分法

//题目：求x的平方根整数部分
        //二分查找
        public static int binarySearch(int x)
        { 
            int index = -1, l =0,r = x;
            while (l <= r)
            { 
                System.out.println("l:"+l+"r:"+r);
                int mid = l + (r - l)/2;
                if(mid * mid == x)
                {   index=mid;
                    return index;}
                //也可以用if (mid * mid <= x) {index = mid;l = mid + 1;}其中index = mid;不能少
               else if(mid * mid < x)
                { 
    index = mid;
                    l = mid + 1;
    
                }
                else
                { 
                    r = mid - 1;
                }
    
            }
            return index;
        }
    
        public static void main(String[] args) { 
            for (int i = 1;i < 26;i ++) { 
                System.out.println(binarySearch(i));
            }
        }

# 斐波那契数列的三种解法 #

第一种：暴力递归  
第二种：去重递归（用一个数组保存之前求出来的值）

public static int ArrayRecurse(int[]arr,int index){ 
            if(index== 0) return 0;
            if(index == 1) return 1;
            if(arr[index] != 0) return arr[index];
    
            arr[index] = ArrayRecurse(arr,index-1)+ArrayRecurse(arr,index-2);
            return arr[index];
        }
        public static int fabonacio(int num){ 
            int[] arr = new int[num+1];
            return ArrayRecurse(arr,num);
        }
    
        public static void main(String[] args) { 
            System.out.println(fabonacio(5));//索引为5的位置的斐波那契排列数
        }

第三种：双指针迭代  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzU4NTc0_size_16_color_FFFFFF_t_70 5]

public static int iterate(int num){ 
    
            if(num == 0) return 0;
            if(num == 1) return 1;
        int low = 0,high = 1;
            for(int i = 2;i <= num;i++)
            { 
                int sum = high+low;
                low = high;
                high = sum;
            }
            return high;
    
    }
        public static void main(String[] args) { 
            System.out.println(iterate(10));//索引为10的位置的斐波那契排列数0 1 1 2 3 5 8 13 21 34 55
        }
    }

# 排列硬币 #

总共有n个硬币，要求第k行必须有k个硬币，给定一个整数，求可形成的完整阶梯行的总行数  
如1 2 3 4，数字10可形成的完整阶梯行的总行数是4，数字11也是4  
法一：

public static int getTotal(int num)
    { 
        int i = 0;
        while(num > i){ 
            i++;
            num = num-i;
         // if(num < i) return i;
        }
        return i;
    }
        public static void main(String[] args) { 
            System.out.println(getTotal(15));//索引为5的位置的斐波那契排列数
        }
    }

法二：二分法

public static int arrange2(int n){ 
    int low = 0,high = n;
    while(low <= high){ 
    int mid = (high - low)/2 + low;
    int cont = ((mid+1)*mid)/2'
    if(cont == n)return mid;
    else if(cont > n) high = mid -1;
    else low = mid+1;
    }
    return high;
    }

[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzU4NTc0_size_16_color_FFFFFF_t_70]: /images/20221005/35a285e1e97447bcba33b5092c983cff.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzU4NTc0_size_16_color_FFFFFF_t_70 1]: /images/20221005/95051c2d940f4f5081d3285beb97a002.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzU4NTc0_size_16_color_FFFFFF_t_70 2]: /images/20221005/f6f9d74b08f246b5b15209651b60e173.png
[20210713022430542.png]: /images/20221005/b788ec141c5443199bd843668ba7b621.png
[20210713023332143.png]: /images/20221005/19f32f014a0548a1920e6529b0a65230.png
[20210713023438746.png]: /images/20221005/668438e23d1d4d4fa93770bf93f70dc5.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzU4NTc0_size_16_color_FFFFFF_t_70 3]: /images/20221005/760f34034b5441c6a0a66ddf3f4d87ce.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzU4NTc0_size_16_color_FFFFFF_t_70 4]: /images/20221005/8ed1551e005b47a496c2c9d0fddf1e0a.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzQxMzU4NTc0_size_16_color_FFFFFF_t_70 5]: /images/20221005/efca560ce4264c219e7f09570005a17d.png