c++常见的几种排序算法总结

原文：c++常见的几种排序算法总结

源代码下载地址： http://www.zuidaima.com/share/1829391352843264.htm

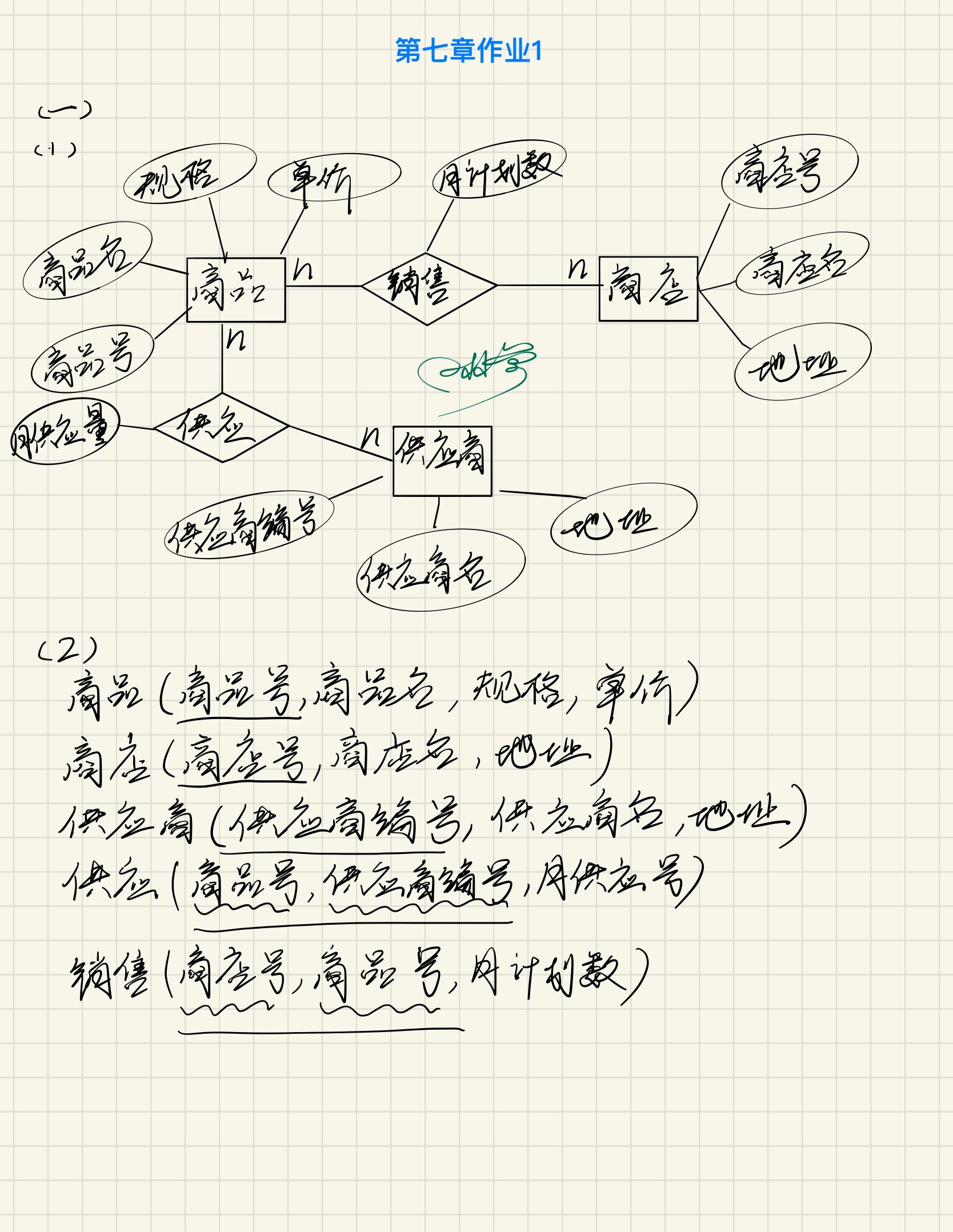
常见的几种排序:冒泡排序、鸡尾酒排序、直接插入排序、折半插入排序、快速排序、桶排序、鸽巢排序、选择排序、奇偶排序、计数排序。

#include "stdafx.h"
#include <stdio.h>
#include<malloc.h>
#include <iostream>
using namespace std;
void swap(int &a,int &b)
{
    int temp = a;
    a = b;
    b = temp;
}
//快速排序
//通过一趟扫描将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,
//然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
void QuickSort(int a[],int low,int high)
{
    if(low >= high)
        return;
    int i = low;
    int j = high;
    int key = a[i];
    while( i < j )//key自动覆盖数组的第一个数据
    {
        //从右向左搜索,直到搜索到的数大于等于开始记录的数,交换其位置
        while(i<j && a[j] >= key) 
            j--;
        if(i<j){
            a[i] = a[j];
        }        
        //从左向右搜索,直到搜索到的数小于等于开始记录的数,交换其位置
        while(i<j && a[i] <= key) 
            i++;
        if(i<j){
            a[j] = a[i];
        }    
    }
    a[i] = key;
    QuickSort(a,low,i-1);
    QuickSort(a,i+1,high);
}
//冒泡排序（bubble sort） — O(n^2）
//用二重循环实现，外循环变量设为i，内循环变量设为j。外循环重复9次，内循环依次重复9，8，...，1次。每次进行比较的两个元素都是与内循环j有关的，
//它们可以分别用a[j]和a[j+1]标识，i的值依次为1,2,...,9，对于每一个i, j的值依次为1,2,...10-i。
void BubbleSort(int a[],int n)
{
    for(int i = 0;i<n-1;i++)
    {
        for(int j = 0;j<n-1-i;j++)
        {
            if(a[j] > a[j+1])
            {
                swap(a[j],a[j+1]);
            }
        }
    }
}
//鸡尾酒排序(Cocktail sort，双向的冒泡排序) — O(n^2）
void CocktailSort(int a[],int n)
{
    int i;
    bool swapped = true;
    while(swapped)
    {
        swapped = false;
        //从左向右扫描,比较相邻两个数
        for( i = 0;i<n-1;i++)
        {
            if(a[i] > a[i+1])
            {
                swap(a[i],a[i+1]);
                swapped = true;
            }
        }
        for( i = n-1;i > 0;i--)
        {
            if(a[i] < a[i-1])
            {
                swap(a[i],a[i-1]);
                swapped = true;
            }
        }
    }
}
//直接插入排序
//将待比较的数值与它的前一个数值进行比较，所以外层循环是从第二个数值开始的。
//当前一数值比待比较数值大的情况下继续循环比较，直到找到比待比较数值小的并将待比较数值置入其后一位置，结束该次循环。
void InsertionSort(int a[],int n)
{
    int temp,i,j;
    for(i = 1 ; i < n;i++)
    {
        if(a[i-1] > a[i])
        {
            temp  = a[i];
            /*j = i;
            while(j >0 && a[j-1] > temp ){//此处类似于冒泡
                a[j] = a[j-1];//向前移动一位
                j--;
            } 
            a[j] = temp;*/
            for(j = i;j>= 0 && a[j-1] >temp;j--)
            {
                a[j] = a[j-1];
                a[j-1] = temp;
            }
        }
    }
}
//折半插入排序(二分插入排序)
//在插入第i个元素时，对前面的0～i-1元素进行折半，先跟他们中间的那个元素比，如果小，则对前半再进行折半，否则对后半进行折半，直到left>right，
//然后再把第i个元素前1位与目标位置之间的所有元素后移，再把第i个元素放在目标位置上。
void BinaryInsertionSort(int a[],int n)
{
    int i,j,left,right,middle,num;
    for(i = 1;i<n;i++)
    {
        left = 0;
        right = i-1;
        num = a[i];
        while(left <= right)
        {
            middle = (left + right)/2;
            if(num >= a[middle])// 在右边插入
            {
                left = middle + 1;
            }else{//在左边插入
                right = middle -1;
            }
        }
        //每次查找完毕后，left总比right大一
        for(j = i;j >= left;j--)
            a[j] = a[j-1];
        a[left] = num;//右移后left位置上为空,把num放置left位置
    }
}
//桶排序 1,桶排序是稳定的 2,桶排序是常见排序里最快的一种,比快排还要快…大多数情况下 3,桶排序非常快,但是同时也非常耗空间,基本上是最耗空间的一种排序算法
void BucketSort(int a[],int n)
{
    int maxVal = a[0]; //假设最大为arr[0]
    for(int x = 1; x < n; x++)  //遍历比较，找到大的就赋值给maxVal
    {
        if(a[x] > maxVal)
            maxVal = a[x];
    }
    int tmpArrLen = maxVal + 1;
    int *tmpArr = new int[tmpArrLen];  //获得空桶大小
    int i, j;
    for( i = 0; i < tmpArrLen; i++)  //空桶初始化
        tmpArr[i] = 0;
    for(i = 0; i < n; i++)   //寻访序列，并且把项目一个一个放到对应的桶子去。
        tmpArr[ a[i] ]++;
    for(i = 0, j = 0; i < tmpArrLen; i++)
    {
        while( tmpArr[ i ] != 0) //对每个不是空的桶子进行排序。
        {
            a[j ] = i;  //从不是空的桶子里把项目再放回原来的序列中。i为索引,数组的索引位置就表示值
            j++;
            tmpArr[i]--;
        }
    }
}
//鸽巢排序 --- 是一种时间复杂度为(Θ(n))且在不可避免遍历每一个元素并且排序的情况下效率最好的一种排序算法. 但它只有在差值（或者可被映射在差值）很小的范围内的数值排序的情况下实用
//原理类似桶排序,同样需要一个很大的鸽巢[桶排序里管这个叫桶,名字无所谓了]
//鸽巢其实就是数组啦,数组的索引位置就表示值,该索引位置的值表示出现次数,如果全部为1次或0次那就是桶排序
void PogeonSort(int a[],int n)
{
    int max = getMaxValue(a,n);
    int *count = (int*)malloc(sizeof(int) *(max+1));
    int i,x,y;
    for(i = 0;i<max+1;i++)
        count[i]=0;
    for(i = 0 ;i < n;i++)
        count[a[i]]++;
    int z=0;
    for(x = 0;x<max+1;x++)
    {
        for(y =0;y<count[x];y++)
        {
            a[z++] = x;
        }
    }
}
//选择排序 直接从待排序数组里选择一个最小(或最大)的数字,每次都拿一个最小数字出来,顺序放入新数组,直到全部拿完
void SelectionSort(int a[],int n)
{
    for(int i = 0;i<=n-1;i++)
    {
        int min = a[i];
        int min_index = i;
        for(int j = i;j <=n-1;j++)
        {
            if(a[j] < min)
            {
                min = a[j];
                min_index = j;
            }
        }
        if(min_index != i)
        {
            swap(a[i],a[min_index]);
        }
    }
}
//奇偶排序 奇数列排一趟序,偶数列排一趟序,再奇数排,再偶数排,直到全部有序
void OddEvenSort(int a[],int n)
{
    //第一次比较奇数列,奇数列与它的邻居偶数列比较
    int flag = 1;
    while(flag)
    {
        flag = 0;
        //奇数列排序
        for(int i = 1;i < n-1;i+=2)
        {
            if(a[i] > a[i+1])
            {
                swap(a[i],a[i+1]);
                flag = 1;
            }
        }
        //偶数列排序
        for(int j = 0;j < n-1;j+=2)
        {
            if(a[j] > a[j+1])
            {
                swap(a[j],a[j+1]);
                flag = 1;
            }
        }
    }
}
//计数排序 这种排序算法，依靠一个辅助数组来实现，不基于比较，算法复杂度为 O(n) ，
//但由于要一个辅助数组C，所以空间复杂度要大一些，由于计算机的内存有限，这种算法不适合范围很大的数的排序。
//注：基于比较的排序算法的最佳平均时间复杂度为 O(nlogn)
void CountSort(int a[],int n)
{
    int t;
    int i, z = 0;
    int max,min,*count;
    //找出数组的最大最小值，确定计数的范围 
     min = max = a[0];
    for(i = 0; i < n; ++i) 
    {
         if(a[i] < min)
             min = a[i];
        else if(a[i] > max)
             max = a[i];
    }
    //分配统计计数数组空间，大小为原数组的数域范围
    //count = (int *)malloc((max-min + 1) * sizeof(int));
    count = (int *)malloc((max + 1) * sizeof(int));
    for(i = 0; i < max + 1; i++) {//for(i = 0; i < max-min + 1; i++)
        count[i] = 0;
    }
    //统计a中每个元素出现的次数，并将次数保存在
    //count[a[i]]中，此处减去min是为了节省统计数组的空间
    for(i = 0; i < n; i++) {
        //count[a[i] - min]++;
        count[a[i]]++;//其实里面是0,1
    }
    //将统计数组还原到a中，其中a范围为min到max
    //此处很好的解决了统计时节省空间减去min造成的不对称问题
    for(t = 0; t <= max; t++) {
        while(count[t]-- >0)
        {
            a[z++] = t;
        }
    }
    free(count);
}
//堆排序 ---调整堆  父节点：parent(i) = i/2; 孩子节点: 左节点：left(i) = 2*i 右节点：right(i) = 2*i + 1;
void HeapAdjust(int a[],int i,int n)
{
    int leftChild = 2 * i; //i的左孩子节点序号 
    int rightChild = 2 * i + 1; //i的右孩子节点序号 
    int max = i;
    if(i <= (n-1)/2)//如果i是叶节点就不用进行调整 
    {
        if(leftChild <= n-1 && a[leftChild] > a[max])
            max = leftChild;
        if(rightChild <= n-1 && a[rightChild] > a[max])
            max = rightChild;
        if(max != i)
        {
            swap(a[i],a[max]);
            HeapAdjust(a,max,n);    //避免调整之后以max为父节点的子树不是堆 
        }
    }
}
//堆排序  ---建立堆
void BuildHeap(int a[],int n)
{
    for(int i = (n-1)/2;i>=0;i--)//非叶节点最大序号值为n/2 
    {
        HeapAdjust(a,i,n);
    }
}
//堆排序 把堆顶的最大数取出,将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现
//剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束
void HeapSort(int a[],int n)
{
    int i ;
    BuildHeap(a,n);
    for(i = n-1;i >= 0;i--)
    {
         swap(a[0],a[i]);        //交换堆顶和最后一个元素，即每次将剩余元素中的最大者放到最后面 
         HeapAdjust(a,0,i);      //重新调整堆顶节点成为大顶堆
    }
}
//打印数组
void showArray(int a[],int len)
{
    for(int i = 0;i<len;i++){
        printf("%d ",a[i]);
    }
}
int _tmain(int argc, _TCHAR* argv[])
{
    int a[]= {9,12,3,10,8,5,2,14,56,76,223,123};
    int len = sizeof(a)/sizeof(int);
    printf("原始数组:\n");
    showArray(a,len);
    printf("\n-------------------------------------\n");
    printf("冒泡排序后数组:\n");
    BubbleSort(a,len);
    showArray(a,len);
    printf("\n-------------------------------------\n");
    printf("鸡尾酒排序后数组:\n");
    CocktailSort(a,len);
    showArray(a,len);
    printf("\n-------------------------------------\n");
    printf("直接插入排序后数组:\n");
    InsertionSort(a,len);
    showArray(a,len);
    printf("\n-------------------------------------\n");
    printf("折半插入排序后数组:\n");
    BinaryInsertionSort(a,len);
    showArray(a,len);
    printf("\n-------------------------------------\n");
    printf("快速排序后数组:\n");
    QuickSort(a,0,len-1);
    showArray(a,len);
    printf("\n-------------------------------------\n");
    printf("桶排序后数组:\n");
    BucketSort(a,len);
    showArray(a,len);
    printf("\n-------------------------------------\n");
    printf("鸽巢排序后数组:\n");
    PogeonSort(a,len);
    showArray(a,len);
    printf("\n-------------------------------------\n");
    printf("选择排序后数组:\n");
    SelectionSort(a,len);
    showArray(a,len);
    printf("\n-------------------------------------\n");
    printf("奇偶排序后数组:\n"); 
    OddEvenSort(a,len);
    showArray(a,len);
    printf("\n-------------------------------------\n");
    printf("计数排序后数组:\n"); 
    CountSort(a,len);
    showArray(a,len);
    printf("\n-------------------------------------\n");
    printf("堆排序后数组:\n"); 
    HeapSort(a,len);
    showArray(a,len);
    printf("\n-------------------------------------\n");
    return 0;
}