1.基本概念

二叉树：一种特殊的树形结构，它的特点是每个结点至多只有两棵子树（即二叉树中不存在度大于2的结点），并且，二叉树的子树有左右之分，其次序不能任意颠倒。

二叉树的五种形态：空二叉树、只有一个根结点、根节点只有左子树、根节点只有右子树、根节点既有左子树又有右子树。

特殊二叉树：

斜树（所有结点只有左子树的二叉树叫左斜树，所有结点只有右子树的二叉树叫右斜树，与线性表结构类似）
满二叉树（所有分支结点都存在左子树和右子树，且所有叶子结点都在同一层，即拥有最大结点数）
完全二叉树（从上到下，从左到右依次填满树结构，若一层没填满，则不能跳到一层。满二叉树为特殊的完全二叉树）

二叉树的性质：

性质1 在二叉树的第i层上至多有2i−1个结点
性质2 深度为k的二叉树至多有2k−1个结点
性质3 对于任何一棵二叉树，如果其叶子结点数为n0，度为2的结点数为n2，则n0=n2+1
性质4 具有n个结点的二叉树，其深度为⌊log2n⌋+1（⌊x⌋不大于x的最大整数）
性质5 如果对于一棵有n个结点的完全二叉树的结点按层序编号（从第1层到⌊log2n⌋+1层，每层从左至右），对任意一结点 i（1≤i≤n）有：

1.  如果i=1，则i是根节点，无双亲。如果i>1，则⌊*i*/2⌋是其双亲结点
2.  如果2i>n，则i结点的无左孩子，否则i结点左孩子为2i
3.  如果2i+1>n，则i结点无右孩子，否则i结点右孩子为2i+1

2.二叉树的存储结构

顺序存储结构

按照完全二叉树的结构，从1开始依次对各结点编号，并根据编号将其存入对应下标的数组中。不存在的结点用“0”或其他符号表示。此类方法对于非完全二叉树，可能会造成大量存储空间的浪费。

链式存储结构（二叉链表）

该存储方法在每个结点中设置两个指针域，分别指向该结点的左孩子和右孩子。

//二叉树的链式存储结构定义 
typedef char TElemType;         //元素的数据类型根据实际情况而定，这里假设为char
typedef struct TNode          //结点结构 
{  
    TElemType      data;           //数据域，用于存储结点数据 
    struct TNode  *lchild;     //指针，指向该结点的左孩子 
    struct TNode  *rchild;     //指针，指向该结点的右孩子 
}BiTNode,*BiTree;

如有需要，还可以增加一个指针域指向双亲，形成三叉链表。

3.二叉树的遍历

二叉树的遍历是从根节点出发，按照某种次序依次访问二叉树中所有结点，使得每个结点被访问一次且仅被访问一次。
二叉树的遍历方式有很多，如果限制从左到右的方向，则主要包括前序遍历、中序遍历、后序遍历和层序遍历
每次遍历时，对各结点的操作，此处定义为最简单的输出操作：

void printelement(TElemType e)  //定义visit函数，最简单的就是print直接输出 
{
    printf("%c",e);
}

前序、中序和后序遍历有递归和非递归两种实现方法。非递归遍历方法需要运用栈这种数据结构，在此定义栈的数据结构以及建栈、压栈、出栈和验证栈是否为空操作：

typedef BiTNode* ElemType;    //定义数据类型为指向树结点的指针
typedef struct Node
{
    ElemType data;
    struct Node*next;
}Node,*LinkStack;
int InitStack(LinkStack*S)
{
    (*S)=(Node*)malloc(sizeof(Node));      //头结点 
    if (!(*S)) return ERROR;
    (*S)->next=NULL;                        
    (*S)->data=0;                         //头结点数据域用来存储栈长度 
}
int StackEmpty(LinkStack S)   //验证栈是否为空 
{
    if (S->data==0) return TRUE;
    return FALSE; 
}
int Push(LinkStack *S,ElemType e)   //将元素e压栈 
{
    Node*p;
    p=(Node*)malloc(sizeof(Node));
    if (!p) return ERROR;
    p->data=e;
    p->next=(*S)->next;
    (*S)->next=p;
    (*S)->data++;
    return OK;
}
int POP(LinkStack *S,ElemType*e)  //将栈顶元素出栈，并将值返回给e 
{
    Node*p;
    if (StackEmpty(*S)) return ERROR;
    p=(*S)->next;
    *e=p->data;
    (*S)->next=p->next;
    free(p);
    (*S)->data--;
    return OK;
}

前序遍历

若二叉树不为空，先访问根结点，然后前序遍历左子树，再前序遍历右子树。

void PreOrderTraverse(BiTree T,void(*visit)(TElemType))  //递归
{
    if (T==NULL) return;
    visit(T->data);
    PreOrderTraverse(T->lchild,visit);
    PreOrderTraverse(T->rchild,visit);
}
void PreOrderTraverse(BiTree T,void(*visit)(TElemType))  //非递归
{
    BiTNode*p;
    LinkStack S;
    InitStack(&S);
    p=T;
    while (p||!StackEmpty(S))     //当树非空或栈不为空时进行遍历操作 
    {
        if (p)                     //当前结点存在时
        {
            Push(&S,p);            //将结点压栈
            visit(p->data);       //访问当前结点
            p=p->lchild;           //指向当前结点的左孩子
        }else
        {
            POP(&S,&p);            //当前结点不存在时，则弹出栈顶结点，使其成为当前结点 
            p=p->rchild;           //指向当前结点的右孩子 
        }
    }
}

中序遍历

若二叉树不为空，先中序遍历左子树，然后访问根结点，再中序遍历右子树。

void InOrderTraverse(BiTree T,void(*visit)(TElemType))  //递归
{
    if (T==NULL) return;
    InOrderTraverse(T->lchild,visit);
    visit(T->data);
    InOrderTraverse(T->rchild,visit);
}
void InOrderTraverse(BiTree T,void(*visit)(TElemType))  //非递归
{
    BiTNode*p;
    LinkStack S;
    InitStack(&S);
    p=T;
    while (p||!StackEmpty(S))      //当树非空或栈不为空时进行遍历操作 
    {
        if (p)                  //当前结点存在时 
        { 
            Push(&S,p);         //将结点压栈 
            p=p->lchild;        //指向当前结点的左孩子 
        }else
        {
            POP(&S,&p);        //当前结点不存在时，则弹出栈顶结点，使其成为当前结点 
            visit(p->data);    //访问当前结点 
            p=p->rchild;       //指向当前结点的右孩子 
        }
    }
}

后序遍历

若二叉树不为空，先后序遍历左子树，然后后序遍历右子树，再访问根结点。

void PostOrderTraverse(BiTree T,void(*visit)(TElemType))  //递归
{
    if (T==NULL) return;
    PostOrderTraverse(T->lchild,visit);
    PostOrderTraverse(T->rchild,visit);
    visit(T->data);
}
void PostOrderTraverse(BiTree T,void(*visit)(TElemType)) //非递归
{
    BiTNode*pcur,*plastvisit;    //pcur为当前结点，plastvisit为上一个访问的结点 
    LinkStack S;
    InitStack(&S);               //建栈 
    pcur=T;                     //使根结点成为当前结点 
    plastvisit=NULL;             
    while(pcur)                 //寻找后序遍历的第一个结点，并将沿路结点依次压栈 
    {
        Push(&S,pcur);
        pcur=pcur->lchild;
    }
    while (!StackEmpty(S))    //栈为空时，所有结点输出完毕，退出循坏 
    {
        POP(&S,&pcur);        //将栈顶结点弹出，成为当前结点 
        if (pcur->rchild==NULL || pcur->rchild==plastvisit) //如果当前结点的右孩子不存在或右孩子已经被访问过，则可以输出该结点 
        {
            visit(pcur->data);
            plastvisit=pcur;   //使当前结点成为上一个访问的结点，为下一轮做准备 
        }else                //否则说明当前结点的右子树还没有遍历，不能输出当前结点 
        {
            Push(&S,pcur);  //将当前结点重新压栈 
            pcur=pcur->rchild;  //进入当前结点的右子树 
            while(pcur)    
            {
                Push(&S,pcur);
                pcur=pcur->lchild;
            }
        }    
    }
}

层序遍历

若二叉树不为空，从树的第一层开始，从左至右，从上至下逐层访问各结点。
和前三种遍历方法相比，层序遍历较为不同，在此借助队列结构来实现遍历。
首先定义队列的数据结构以及建队、入队、出队和验证队列是否为空的操作：

typedef BiTNode* ElemType; //定义数据类型为指向树结点的指针
typedef struct Node   
{  
    ElemType data;            //数据域，用于存储结点数据 
    struct Node *next;        //指针域，存储下一个结点的地址信息 
}QNode,*Queueptr;  
typedef struct  
{  
    Queueptr front,rear;     //定义头指针和尾指针 
}LinkQueue;
int InitQueue(LinkQueue*Q)    //建立队列 
{  
    Q->front=(QNode*)malloc(sizeof(QNode));   //建立头结点 
    if (!Q->front) return ERROR;  
    Q->front->next=NULL;     
    Q->rear=Q->front;           //头尾指针同时指向头结点，队列为空 
    return OK;  
}
int QueueEmpty(LinkQueue*Q)  //验证队列是否为空 
{  
    if (Q->front==Q->rear) return TRUE;  
    return FALSE;   
}
int EnQueue(LinkQueue*Q,ElemType e)  //插入元素e队列 
{  
    QNode*p;  
    if (!Q->front) return ERROR;  
    p=(QNode*)malloc(sizeof(QNode));  
    p->data=e;  
    p->next=NULL;                  //使新节点next指针指向空 
    Q->rear->next=p;               //使前一结点指向新节点 
    Q->rear=p;                     //使尾指针指向新节点 
}  
int DeQueue(LinkQueue*Q,ElemType*e)  //删除队头元素，返回值给e 
{  
    QNode*p;  
    if (!Q->front) return ERROR;  
    p=Q->front->next;                //记录队头结点 
    *e=p->data;  
    Q->front->next=p->next;          //将头结点指向队头结点的下一个结点 
    if (Q->rear==p) Q->rear=Q->front;  //若队头结点为最后一个结点，则使尾指针指向头结点 
    free(p);                          //释放队头结点 
    return OK;  
}

层序遍历：

void LevelOrderTraverse(BiTree T,void(*visit)(TElemType))
{
    BiTNode*p;
    LinkQueue Q;        //定义队列类型 
    InitQueue(&Q);     //创建队列 
    if (T!=NULL) EnQueue(&Q,T);   //如果树非空，把根结点入队列 
    while(!QueueEmpty(&Q))     //如果队列非空，则继续遍历操作 
    {
        DeQueue(&Q,&p);      //将队列头的树结点弹出 
        visit(p->data);      //对出队列的结点进行访问 
        if (p->lchild)       //如果该出队列的结点左孩子存在，则将其左孩子入队列 
        EnQueue(&Q,p->lchild);
        if (p->rchild)      //如果该出队列的结点右孩子存在，则将其右孩子入队列 
        EnQueue(&Q,p->rchild);
    }
}

4.二叉树的建立

前面我们了解了几种基本的二叉树遍历方法，现在我们就可以运用这些方法来建立二叉树。只需把前面遍历过程中对每个结点的输出操作改为输入操作即可。例如用前序遍历的方法建立二叉树：

//二叉树的建立
void CreateBiTree(BiTree * T)
{
    char ch;
    scanf("%c",&ch);
    if (ch=='#') *T=NULL;    //如果结点数据为空，则将指针指向空 
    else
    {
        *T=(BiTree)malloc(sizeof(BiTNode));  //申请结点空间 
        if (!*T) exit(OVERFLOW);
        (*T)->data=ch;                       //输入数据，生成根节点 
        CreateBiTree(&((*T)->lchild)); //构造左子树 CreateBiTree(&((*T)->rchild)); //构造右子树 } }

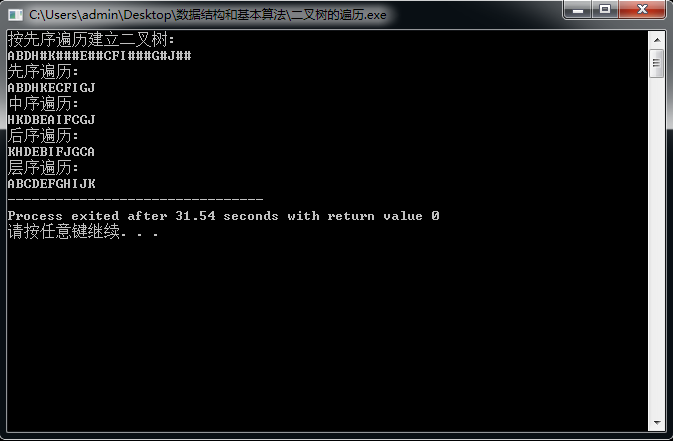
5.代码验证

int main()
{
    BiTree T;
    printf("按先序遍历建立二叉树:\n");
    CreateBiTree(&T);
    printf("先序遍历:\n");
    PreOrderTraverse(T,printelement);
    printf("\n中序遍历:\n");
    InOrderTraverse(T,printelement);
    printf("\n后序遍历:\n");
    PostOrderTraverse(T,printelement);
    printf("\n层序遍历:\n");
    LevelOrderTraverse(T,printelement);
    return 0;
}