图像处理之高斯混合模型

太过爱你忘了你带给我的痛 2022-06-15 06:52 190阅读 0赞

**图像处理之高斯混合模型**

**一：概述**

高斯混合模型(GMM)在图像分割、对象识别、视频分析等方面均有应用，对于任意给定的数据样本集合，根据其分布概率， 可以计算每个样本数据向量的概率分布，从而根据概率分布对其进行分类，但是这些概率分布是混合在一起的，要从中分离出单个样本的概率分布就实现了样本数据聚类，而概率分布描述我们可以使用高斯函数实现，这个就是高斯混合模型-GMM。

![20170526170138039][]

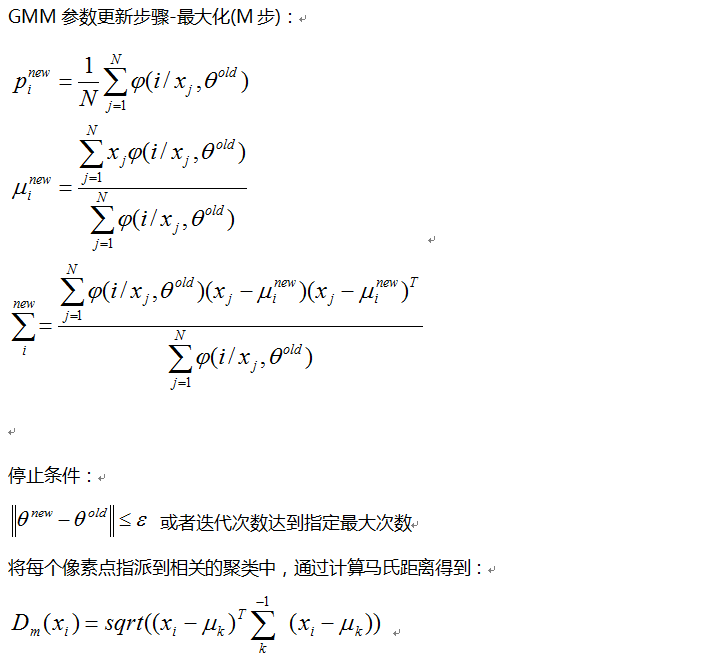
![20170526170352714][]

这种方法也称为D-EM即基于距离的期望最大化。

**三：算法步骤**

1.初始化变量定义-指定的聚类数目K与数据维度D

2.初始化均值、协方差、先验概率分布

3.迭代E-M步骤

\- E步计算期望

\- M步更新均值、协方差、先验概率分布

\-检测是否达到停止条件（最大迭代次数与最小误差满足），达到则退出迭代，否则继续E-M步骤

4.打印最终分类结果

**四：代码实现**

package com.gloomyfish.image.gmm;
    
    import java.util.ArrayList;
    import java.util.Arrays;
    import java.util.List;
    
    /**
     * 
     * @author gloomy fish
     *
     */
    public class GMMProcessor {
    	public final static double MIN_VAR = 1E-10;
    	public static double[] samples = new double[]{10, 9, 4, 23, 13, 16, 5, 90, 100, 80, 55, 67, 8, 93, 47, 86, 3};
    	private int dimNum;
    	private int mixNum;
    	private double[] weights;
    	private double[][] m_means;
    	private double[][] m_vars;
    	private double[] m_minVars;
    
    	/***
    	 * 
    	 * @param m_dimNum - 每个样本数据的维度， 对于图像每个像素点来说是RGB三个向量
    	 * @param m_mixNum - 需要分割为几个部分，即高斯混合模型中高斯模型的个数
    	 */
    	public GMMProcessor(int m_dimNum, int m_mixNum) {
    		dimNum = m_dimNum;
    		mixNum = m_mixNum;
    		weights = new double[mixNum];
    		m_means = new double[mixNum][dimNum];
    		m_vars = new double[mixNum][dimNum];
    		m_minVars = new double[dimNum];
    	}
    	
    	/***
    	 * data - 需要处理的数据
    	 * @param data
    	 */
    	public void process(double[] data) {
    		int m_maxIterNum = 100;
    		double err = 0.001;
    		
    		boolean loop = true;
    		double iterNum = 0;
    		double lastL = 0;
    		double currL = 0;
    		int unchanged = 0;
    		
    		initParameters(data);
    		
    		int size = data.length;
    		double[] x = new double[dimNum];
    		double[][] next_means = new double[mixNum][dimNum];
    		double[] next_weights = new double[mixNum];
    		double[][] next_vars = new double[mixNum][dimNum];
    		List<DataNode> cList = new ArrayList<DataNode>();
    
    		while(loop) {
    			Arrays.fill(next_weights, 0);
    			cList.clear();
    			for(int i=0; i<mixNum; i++) {
    				Arrays.fill(next_means[i], 0);
    				Arrays.fill(next_vars[i], 0);
    			}
    			
    			lastL = currL;
    			currL = 0;
    			for (int k = 0; k < size; k++)
    			{
    				for(int j=0;j<dimNum;j++)
    					x[j]=data[k*dimNum+j];
    				double p = getProbability(x); // 总的概率密度分布
    				DataNode dn = new DataNode(x);
    				dn.index = k;
    				cList.add(dn);
    				double maxp = 0;
    				for (int j = 0; j < mixNum; j++)
    				{
    					double pj = getProbability(x, j) * weights[j] / p; // 每个分类的概率密度分布百分比
    					if(maxp < pj) {
    						maxp = pj;
    						dn.cindex = j;
    					}
    	
    					next_weights[j] += pj; // 得到后验概率
    	
    					for (int d = 0; d < dimNum; d++)
    					{
    						next_means[j][d] += pj * x[d];
    						next_vars[j][d] += pj* x[d] * x[d];
    					}
    				}
    	
    				currL += (p > 1E-20) ? Math.log10(p) : -20;
    			}
    			currL /= size;
    			
    			// Re-estimation: generate new weight, means and variances.
    			for (int j = 0; j < mixNum; j++)
    			{
    				weights[j] = next_weights[j] / size;
    	
    				if (weights[j] > 0)
    				{
    					for (int d = 0; d < dimNum; d++)
    					{
    						m_means[j][d] = next_means[j][d] / next_weights[j];
    						m_vars[j][d] = next_vars[j][d] / next_weights[j] - m_means[j][d] * m_means[j][d];
    						if (m_vars[j][d] < m_minVars[d])
    						{
    							m_vars[j][d] = m_minVars[d];
    						}
    					}
    				}
    			}
    			
    			// Terminal conditions
    			iterNum++;
    			if (Math.abs(currL - lastL) < err * Math.abs(lastL))
    			{
    				unchanged++;
    			}
    			if (iterNum >= m_maxIterNum || unchanged >= 3)
    			{
    				loop = false;
    			}
    		}
    		
    		// print result
    		System.out.println("=================最终结果=================");
    		for(int i=0; i<mixNum; i++) {
    			for(int k=0; k<dimNum; k++) {
    				System.out.println("[" + i + "]: ");
    				System.out.println("means : " + m_means[i][k]);
    				System.out.println("var : " + m_vars[i][k]);
    				System.out.println();
    			}
    		}
    		
    		
    		// 获取分类
    		for(int i=0; i<size; i++) {
    			System.out.println("data[" + i + "]=" + data[i] + " cindex : " + cList.get(i).cindex);
    		}
    		
    	}
    	
    	/**
    	 * 
    	 * @param data
    	 */
    	private void initParameters(double[] data) {
    		// 随机方法初始化均值
    		int size = data.length;
    		for (int i = 0; i < mixNum; i++)
    		{
    			for (int d = 0; d < dimNum; d++)
    			{
    				m_means[i][d] = data[(int)(Math.random()*size)];
    			}
    		}
    		
    		// 根据均值获取分类
    		int[] types = new int[size];
    		for (int k = 0; k < size; k++)
    		{
    			double max = 0;
    			for (int i = 0; i < mixNum; i++)
    			{
    				double v = 0;
    				for(int j=0;j<dimNum;j++) {
    					v += Math.abs(data[k*dimNum+j] - m_means[i][j]);
    				}
    				if(v > max) {
    					max = v;
    					types[k] = i;
    				}
    			}
    		}
    		double[] counts = new double[mixNum];
    		for(int i=0; i<types.length; i++) {
    			counts[types[i]]++;
    		}
    		
    		// 计算先验概率权重
    		for (int i = 0; i < mixNum; i++)
    		{
    			weights[i] = counts[i] / size;
    		}
    		
    		// 计算每个分类的方差
    		int label = -1;
    		int[] Label = new int[size];
    		double[] overMeans = new double[dimNum];
    		double[] x = new double[dimNum];
    		for (int i = 0; i < size; i++)
    		{
    			for(int j=0;j<dimNum;j++)
    				x[j]=data[i*dimNum+j];
    			label=Label[i];
    
    			// Count each Gaussian
    			counts[label]++;
    			for (int d = 0; d < dimNum; d++)
    			{
    				m_vars[label][d] += (x[d] - m_means[types[i]][d]) * (x[d] - m_means[types[i]][d]);
    			}
    
    			// Count the overall mean and variance.
    			for (int d = 0; d < dimNum; d++)
    			{
    				overMeans[d] += x[d];
    				m_minVars[d] += x[d] * x[d];
    			}
    		}
    
    		// Compute the overall variance (* 0.01) as the minimum variance.
    		for (int d = 0; d < dimNum; d++)
    		{
    			overMeans[d] /= size;
    			m_minVars[d] = Math.max(MIN_VAR, 0.01 * (m_minVars[d] / size - overMeans[d] * overMeans[d]));
    		}
    
    		// Initialize each Gaussian.
    		for (int i = 0; i < mixNum; i++)
    		{
    
    			if (weights[i] > 0)
    			{
    				for (int d = 0; d < dimNum; d++)
    				{
    					m_vars[i][d] = m_vars[i][d] / counts[i];
    
    					// A minimum variance for each dimension is required.
    					if (m_vars[i][d] < m_minVars[d])
    					{
    						m_vars[i][d] = m_minVars[d];
    					}
    				}
    			}
    		}
    		
    		System.out.println("=================初始化=================");
    		for(int i=0; i<mixNum; i++) {
    			for(int k=0; k<dimNum; k++) {
    				System.out.println("[" + i + "]: ");
    				System.out.println("means : " + m_means[i][k]);
    				System.out.println("var : " + m_vars[i][k]);
    				System.out.println();
    			}
    		}
    		
    	}
    
    	/***
    	 * 
    	 * @param sample - 采样数据点
    	 * @return 该点总概率密度分布可能性
    	 */
    	public double getProbability(double[] sample)
    	{
    		double p = 0;
    		for (int i = 0; i < mixNum; i++)
    		{
    			p += weights[i] * getProbability(sample, i);
    		}
    		return p;
    	}
    
    	/**
    	 * Gaussian Model -> PDF
    	 * @param x - 表示采样数据点向量
    	 * @param j - 表示对对应的第J个分类的概率密度分布
    	 * @return - 返回概率密度分布可能性值
    	 */
    	public double getProbability(double[] x, int j)
    	{
    		double p = 1;
    		for (int d = 0; d < dimNum; d++)
    		{
    			p *= 1 / Math.sqrt(2 * 3.14159 * m_vars[j][d]);
    			p *= Math.exp(-0.5 * (x[d] - m_means[j][d]) * (x[d] - m_means[j][d]) / m_vars[j][d]);
    		}
    		return p;
    	}
    	
    	public static void main(String[] args) {
    		GMMProcessor filter = new GMMProcessor(1, 2);
    		filter.process(samples);
    		
    	}
    }

结构类DataNode

package com.gloomyfish.image.gmm;
    
    public class DataNode {
    	public int cindex; // cluster
    	public int index;
    	public double[] value;
    	
    	public DataNode(double[] v) {
    		this.value = v;
    		cindex = -1;
    		index = -1;
    	}
    }

**五：结果**

![SouthEast][]

这里初始中心均值的方法我是通过随机数来实现，GMM算法运行结果跟初始化有很大关系，常见初始化中心点的方法是通过K-Means来计算出中心点。大家可以尝试修改代码基于K-Means初始化参数，我之所以选择随机参数初始，主要是为了省事！

**不炒作概念，只分享干货！**

**请继续关注本博客！**

[20170526170138039]: /images/20220615/62369e3fa7034982a00fd601830a2eb0.png
[20170526170352714]: /images/20220615/16b66ca0f7d8461493903b894456c793.png
[SouthEast]: /images/20220615/ca92baa1406547caa4653d0b6ba13538.png