8皇后以及N皇后算法探究，回溯算法的JAVA实现，递归方案

川长思鸟来 2022-05-22 08:43 163阅读 0赞

原文地址：[https://www.cnblogs.com/newflydd/p/5091646.html][https_www.cnblogs.com_newflydd_p_5091646.html]

八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。 高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。计算机发明后，有多种计算机语言可以解决此问题。———以上节选自百度百科。

算法思考，初步思路：

构建二维int或者short型数组，内存中模拟棋盘

chess\[r\]\[c\]=0表示：r行c列没有皇后，chess\[r\]\[c\]=1表示：r行c列位置有一个皇后

从第一行第一列开始逐行摆放皇后

依题意每行只能有一个皇后，遂逐行摆放，每行一个皇后即可

摆放后立即调用一个验证函数（传递整个棋盘的数据），验证合理性，安全则摆放下一个，不安全则尝试摆放这一行的下一个位置，直至摆到棋盘边界

当这一行所有位置都无法保证皇后安全时，需要回退到上一行，清除上一行的摆放记录，并且在上一行尝试摆放下一位置的皇后（回溯算法的核心）

当摆放到最后一行，并且调用验证函数确定安全后，累积数自增1，表示有一个解成功算出

验证函数中，需要扫描当前摆放皇后的左上，中上，右上方向是否有其他皇后，有的话存在危险，没有则表示安全，并不需要考虑当前位置棋盘下方的安全性，因为下面的皇后还没有摆放

回溯算法的天然实现是使用编译器的递归函数，但是其性能令人遗憾

下面我们使用上面的思路初步实现8皇后的问题解法，并且将所有解法打印出来，供我们验证正确性

import java.util.Date;
    
    
    /** * 在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击， * 即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。 * 下面使用递归方法解决 * @author newflydd@189.cn * */
    public class EightQueen { 
        private static final short N=8;        //使用常量来定义，方便之后解N皇后问题
        private static int count=0;            //结果计数器
    
        public static void main(String[] args) {
            Date begin =new Date();
            //初始化棋盘，全部置0
            short chess[][]=new short[N][N];
            for(int i=0;i<N;i++){
                for(int j=0;j<N;j++){
                    chess[i][j]=0;
                }
            }
    
            putQueenAtRow(chess,0);
            Date end =new Date();
            System.out.println("解决 " +N+ " 皇后问题，用时：" +String.valueOf(end.getTime()-begin.getTime())+ "毫秒，计算结果："+count);
        }
    
        private static void putQueenAtRow(short[][] chess, int row) {        
            /** * 递归终止判断：如果row==N，则说明已经成功摆放了8个皇后 * 输出结果，终止递归 */
            if(row==N){
                count++;
                System.out.println("第 "+ count +" 种解：");
                for(int i=0;i<N;i++){
                    for(int j=0;j<N;j++){
                        System.out.print(chess[i][j]+" ");
                    }
                    System.out.println();
                }
                return;
            }
    
            short[][] chessTemp=chess.clone();
    
            /** * 向这一行的每一个位置尝试排放皇后 * 然后检测状态，如果安全则继续执行递归函数摆放下一行皇后 */
            for(int i=0;i<N;i++){
                //摆放这一行的皇后，之前要清掉所有这一行摆放的记录，防止污染棋盘
                for(int j=0;j<N;j++)
                    chessTemp[row][j]=0;
                chessTemp[row][i]=1;
    
                if( isSafety( chessTemp,row,i ) ){
                    putQueenAtRow(chessTemp,row+1);
                }
            }
        }
    
        private static boolean isSafety(short[][] chess,int row,int col) {
            //判断中上、左上、右上是否安全
            int step=1;
            while(row-step>=0){
                if(chess[row-step][col]==1)                //中上
                    return false;
                if(col-step>=0 && chess[row-step][col-step]==1)        //左上
                    return false;
                if(col+step<N && chess[row-step][col+step]==1)        //右上
                    return false;
    
                step++;
            }
            return true;
        }
    }

输出结果：  
![这里写图片描述][70]

需要打印棋盘时，耗时34毫秒，再看一看不需要打印棋盘时的性能：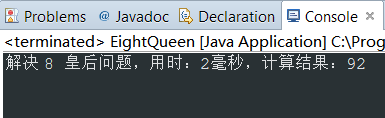  
![这里写图片描述][70 1]

耗时2毫秒，性能感觉还可以。

你以为到这儿就结束了吗？高潮还没开始，下面我们来看看这种算法解决9、10、11…15皇后问题的性能

稍微变动一下代码，循环打印出各个解的结果，如下图所示：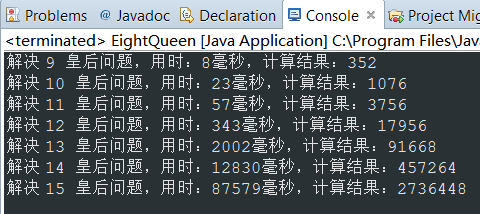  
![这里写图片描述][70 2]

当我开始尝试解决16皇后问题时，发现时间复杂度已经超出我的心里预期，最终没让它继续执行下去。

上网一查N皇后的国际记录，已经有科研单位给出了25皇后的计算结果，耗时暂未可知

我们的程序跑16皇后已经无能为力，跑15皇后已经捉襟见肘（87秒）

中国的一些算法高手能在100秒内跑16皇后，可见上面的算法效率只能说一般，辣么，该如何改进呢？

我们发现二维棋盘数据在内存中浪费严重，全是0和1的组成，同时每次递归时使用JAVA的clone函数克隆一个新的棋盘，消耗进一步扩大，这里面一定有改进的方案。

我们考虑将二维数组使用一维数组代替，将一维数组的下标数据利用起来，模仿棋盘结构，如chess\[R\]=C时，表示棋盘上R行C列有一个皇后

这样程序的空间效率会得到迅速提高，同时二维数据改变成一维数据后的遍历过程也会大为缩减，时间效率有所提高，下面贴出代码：

import java.util.Date;
    
    
    public class EightQueen2 { 
        private static final short K=15;        //使用常量来定义，方便之后解N皇后问题
        private static int count=0;            //结果计数器
        private static short N=0;
    
        public static void main(String[] args) {
            for(N=9;N<=K;N++){
                Date begin =new Date();
                /** * 初始化棋盘，使用一维数组存放棋盘信息 * chess[n]=X:表示第n行X列有一个皇后 */
                short chess[]=new short[N];
                for(int i=0;i<N;i++){
                    chess[i]=0;
                }
    
                putQueenAtRow(chess,(short)0);
                Date end =new Date();
                System.out.println("解决 " +N+ "皇后问题，用时：" +String.valueOf(end.getTime()-begin.getTime())+ "毫秒，计算结果："+count);
            }
        }
    
        private static void putQueenAtRow(short[] chess, short row) {        
            /** * 递归终止判断：如果row==N，则说明已经成功摆放了8个皇后 * 输出结果，终止递归 */
            if(row==N){
                count++;
    // System.out.println("第 "+ count +" 种解：");
    // for(int i=0;i<N;i++){ 
    // for(int j=0;j<N;j++){ 
    // System.out.print(chess[i][j]+" ");
    // }
    // System.out.println();
    // }
                return;
            }
    
            short[] chessTemp=chess.clone();
    
            /** * 向这一行的每一个位置尝试排放皇后 * 然后检测状态，如果安全则继续执行递归函数摆放下一行皇后 */
            for(short i=0;i<N;i++){
                //摆放这一行的皇后
                chessTemp[row]=i;
    
                if( isSafety( chessTemp,row,i ) ){
                    putQueenAtRow(chessTemp,(short) (row+1));
                }
            }
        }
    
        private static boolean isSafety(short[] chess,short row,short col) {
            //判断中上、左上、右上是否安全
            short step=1;
            for(short i=(short) (row-1);i>=0;i--){
                if(chess[i]==col)    //中上
                    return false;
                if(chess[i]==col-step)    //左上
                    return false;
                if(chess[i]==col+step)    //右上
                    return false;
    
                step++;
            }
    
            return true;
        }
    }

运算结果：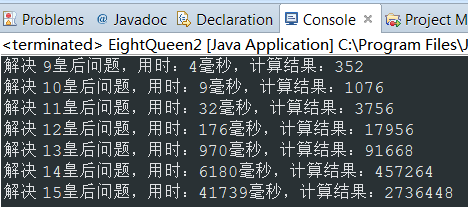  
![这里写图片描述][70 3]  
可以看到所有结果的耗时缩短了一倍有余，这无疑是一次算法的进步

[https_www.cnblogs.com_newflydd_p_5091646.html]: https://www.cnblogs.com/newflydd/p/5091646.html
[70]: /images/20220522/5ba4f89338b14b9d8a84d00950d8eabf.png
[70 1]: /images/20220522/10bd07853ccb4e37aa4b4df84edd2949.png
[70 2]: /images/20220522/a88993fb649143bf8cd0bc5399377375.png
[70 3]: /images/20220522/16b90dffc158467789edf0200b50923f.png