【数据结构】七种常见排序算法详解（直接插入、希尔、选择、冒泡、快速，归并、堆排序）

悠悠 2022-05-21 22:49 235阅读 0赞

## 一、什么是排序？ ##

\*\*【1】排序：\*\*就是将一组杂乱无章的数据按照一定的规律(升序或降序)组织起来。  
\*\*数据表：\*\*待排序数据元素的有限集合。  
**排序码：通常数据元素有多个属性域，其中有一个属性域可用来区分元素，作为排序依据，该域 即为排序码。  
如果在数据表中各个元素的排序码互不相同，这种排序码称为主排序码**。

*  按照主排序码进行排序，排序的结果是唯一的。
 *  按照次排序码进行排序，排序的结果可能是不唯一的。

## 二、排序分类 ##

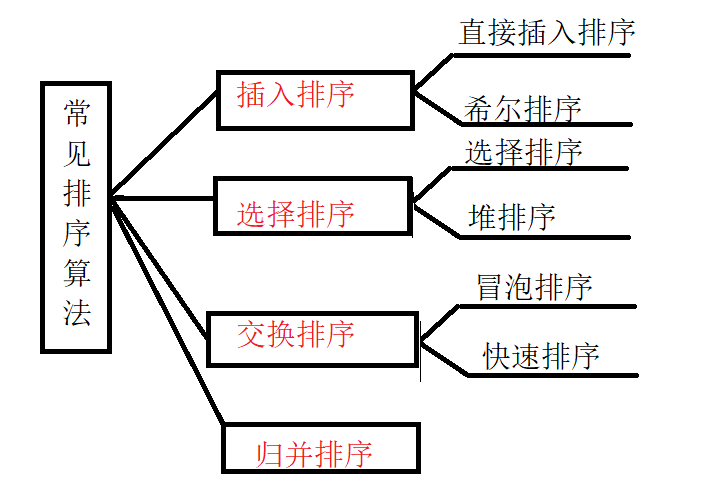
![这里写图片描述][70]

## 三、预备知识 ##

简单的说就是将一组数中相等的数经过某种排序算法后，依然能够保持它在排序之前的相对次序，就称该方法是稳定的，反之为稳定；  
**（1）稳定排序的示意图如下：**  
![这里写图片描述][70 1]  
**（2）内排序和外排序**  
在排序过程中，所有需要排序的数据都一次性加载到内存中，并在内存中调整他们的顺序，称之为**内排序**；如果数据较大，只有部分被调入到内存，并借助内存调整在内存外中存放顺序，成为**外排序**；

**（3）时间复杂度和空间复杂度**  
所谓的算法时间复杂度，就是指执行该算法所需要的计算工作量，空间复杂度就是执行该算法所需要的内存空间。

## 四、七种算法详解 ##

\#\#\#【1】直接插入排序  
**（1）算法思想**  
在待排序的一组数中，假设前面n-1(n>=2)个数已经排好序了，现在要将第n个数插入到前面的n-1个有序数中，使得这n个数是排好序的，如此反复循环，直到全部排好序；

**（2）算法性质**

*  直接排序是稳定的;
 *  算法的时间复杂度为O(n^2);
 *  适用于量小、接近有序的数据

**（3）算法示意图**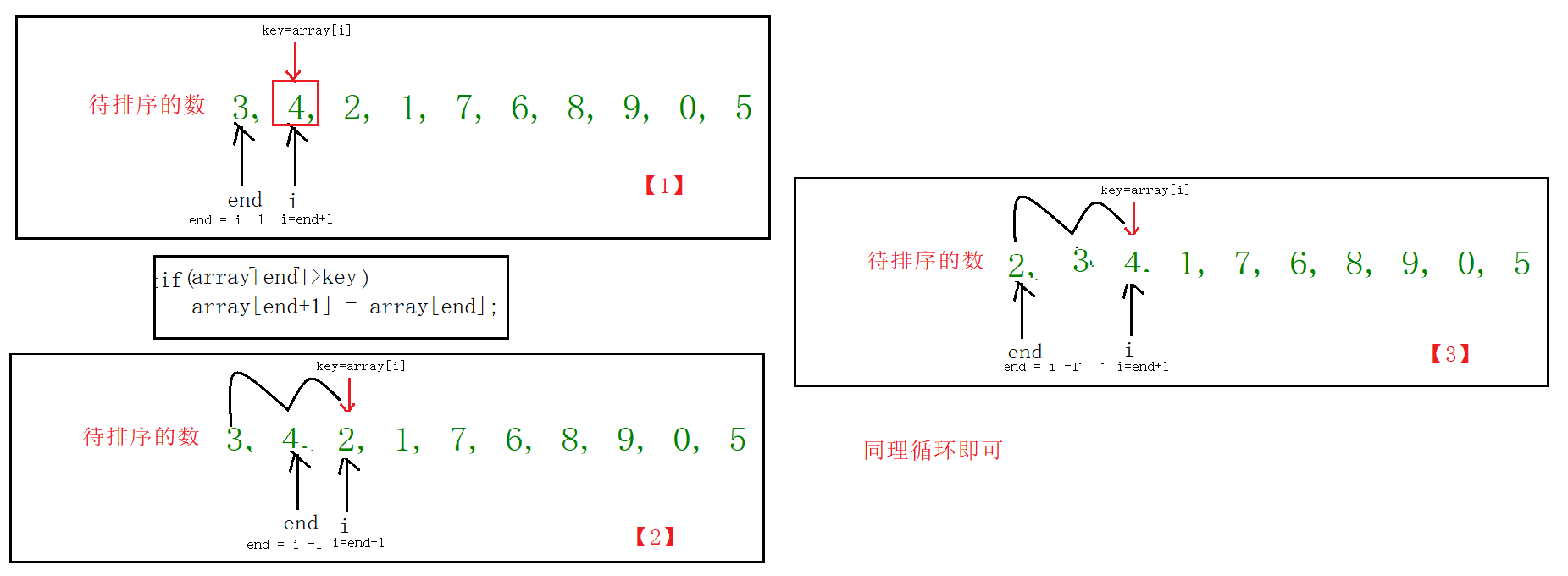  
![这里写图片描述][70 2]

**（4）程序代码**

#include<iostream>
    using namespace std;
    
    template<typename T>
    void Insert_sort(T *array,int len)//排序函数
    {
    	int key;
    	int end;
    	for(int i = 1; i < len ;i++)
    	{
    		key = array[i];
    		for(end = i-1; (end>=0) && array[end] >key ;end--)
    		{
    			array[end+1] = array[end];
    		}
    
    		array[end+1] = key;
    	}
    }
    template<typename T>
    void Print( T array,int len )//打印函数
    {
    	for(int i = 0;i <len ;i++)
    	{
    		cout<<array[i]<<endl;
    	}
    }
    
    int main()
    {
    	int array[10] = {3,4,2,1,7,6,8,9,0,5};
    	int len = sizeof(array)/sizeof(array[0]);
    	Insert_sort(array, len);
    	Print(array,len );
    	return 0;
    }

**（5）结果展示**  
![这里写图片描述][70 3]

\#\#\#【2】希尔排序  
**（1）算法思想**  
在直接排序中，使有序序列只增加一个节点，并且对插入下一个数没有任何关联，所以希尔排序就是对直接排序的一种改进。希尔算法是将一组数按某个增量gap分为若干个组，每组中的下标相差gap，对每组中在进行排序，当gap=1时，整个要排序的数就被分成一组，排序完成。

**（2）算法性质**

*  直接排序是不稳定的;
 *  算法的时间复杂度为O(n^1.3);
 *  适用于量大、接近有序的数据  
    **（3）算法示意图**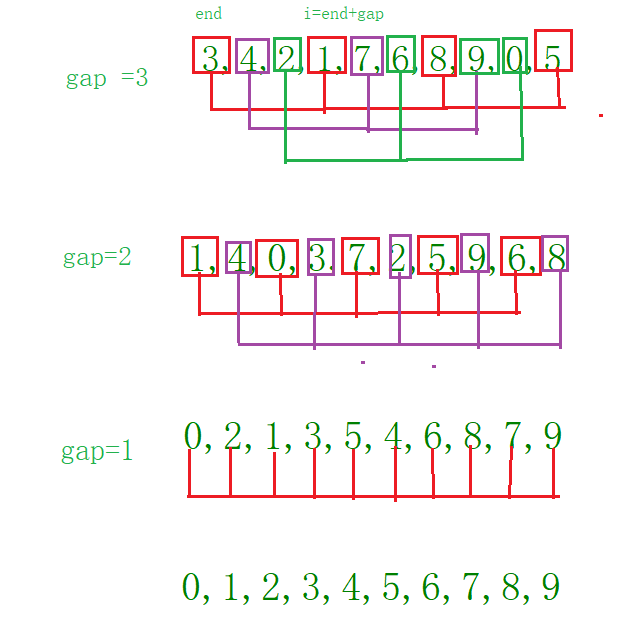  
    ![这里写图片描述][70 4]  
    **（4）程序代码**

#include<iostream>
    using namespace std;
    
    template<typename T>
    void Shell_Sort(T *array,int len)
    {
    	int gap = len ;
    	int key;
    	int end;
    	do
    	{
    		gap = gap/3 +1;
    		gap =1;
    		for(int i = gap; i<len; i+=gap)
    		{
    			key = array[i];
    		
    			for(end = i-gap; (end >= 0)&&(array[end]>key);end-=gap )
    			{
    				array[end+gap] = array[end];
    			}
    			array[end+gap] = key;
    		}
    	}while(gap>1);
    }
    
    template<typename T>
    void Print( T array,int len )
    {
    	for(int i = 0;i <len ;i++)
    	{
    		cout<<array[i]<<endl;
    	}
    }
    
    int main()
    {
    	int array[10] = {3,4,2,1,7,6,8,9,0,5};
    	//char array[] = "sacbfdeghjioznm";
    	int len = sizeof(array)/sizeof(array[0]);
    
    	Shell_Sort(array, len);
    	Print(array,len );
    
    	return 0;
    }

**(5)结果展示**  
![这里写图片描述][70 5]

\#\#\#【3】选择排序  
**（1）算法思想**  
在待排序的一组数中，按住一个数不动，将其与剩下的每一个数比较，如果满足条件，则交换，否则继续比较如此循环上述步骤，直至每个数都排好序；

**（2）算法示意图**  
![这里写图片描述][70 6]  
**（3）程序代码**

#include<iostream>
    using namespace std;
    template<typename T>
    void printArray01(T array[], int len)
    {
    	int i = 0;
    	for(i=0; i<len; i++)
    	{
    		cout<<array[i]<<endl;
    	}
    }
    template<typename T>
    void myswap(T array[],int i,int j)
    {
    				int tmp = array[i];
    				array[i] = array[j];
    				array[j] = tmp;
    }
    template<typename T>
    void select_sort(T array[],int size)
    {
    	int min;
    	for(int i = 0; i<size;i++)
    	{
    		min = i;
    		for(int j= i+1;j<size;j++)
    		{
    			if(array[j] <array[min])
    			{
    				min = j;
    			}
    		}
    		myswap(array,i,min);
    	}
    }
    
    int main()
    {
    	//int buf[10]={2,3,4,1,6,5,7,8,0,9};
    	char buf[] = "sacbfdeghjioznm";
    	int len = sizeof(buf)/sizeof(buf[0]);
    	
    	select_sort(buf,len);
    
    	printArray01(buf,len);
    	return 0;
    }

**（4）结果展示**  
![这里写图片描述][70 7]  
\#\#\#【4】冒泡排序  
**（1）算法思想**  
冒泡排序是较为常用的方法，它是相邻元素之间进行比较，交换，一趟排序下来，找到该组数据中最大（最小的元素），接下来，再在剩下的数中比较，找次大元素，直至所有的数都排好序为止；  
**（2）算法示意图**  
![这里写图片描述][70 8]

**（3）程序代码**

#include<iostream>
    #include<vector>
    using namespace std;
    
    template<typename T>
    void bubble_sort(T *array, int len)
    {
    	int tmp;
    	int exchange = 1;
    	for(int i = 0; (i<len)&& exchange ;i++)
    	{
    		exchange  = 0;
    		for(int j = len -1;j > 0 ;j --)
    		{
    			if(array[j]<array[j-1])
    			{
    				tmp = array[j];
    				array[j] = array[j-1];
    				array[j-1] = tmp;
    				exchange = 1;
    			}
    		}
    	}
    }
    template<typename T>
    void Print( T array,int len )
    {
    	for(int i = 0;i <len ;i++)
    	{
    		cout<<array[i]<<endl;
    	}
    }
    
    int main()
    {
    	//int array[10] = {3,4,2,1,7,6,8,9,0,5};
    	char array[] = "sacbfdeghjioznm";
    	int len = sizeof(array)/sizeof(array[0]);
    
    	bubble_sort(array, len);
    
    	Print(array,len );
    
    	return 0;
    }

**（4）结果展示**  
![这里写图片描述][70 9]

\#\#\#【5】快速排序  
**（1）算法思想**  
在待排序的一组数中，随机找一个数，将它作为枢轴，然后，将该组数据分为两部分，一部分比它大，另一部分比它小，如果要求该组数据是升序排列，那么，就将比它小的数放在该数的左边，把比它大的数放在他的后面，循环往复。。。  
**（2）算法示意图**  
![这里写图片描述][70 10]  
**（3）程序代码**

#include<iostream>
    using namespace std;
    void Swap66(int *array,int low , int high)
    {
    	int tmp= array[low];
    	array[low] =array[high];
    	array[high] = tmp;
    }
    
    int partion(int *array, int low,  int high)
    {
    	int qv  = array[low];
    	while(low < high)
    	{
    		while((low<high) && (qv < array[high]))
    		{
    			high--;
    		}
    
    		Swap66(array, low ,high);
    		while( (low<high)&& (qv>=array[low] ) )
    		{
    			low++;
    		}
    		Swap66(array, low ,high);
    	}
    	return low;
    }
    
    void _sort(int* array,int low,int high)
    {
    	if(low<high)//注意条件必须加！！！！！！！！！！
    	{
    		int qv = partion(array, low, high);
    		_sort(array, low , qv-1 );
    		_sort(array, qv+1, high);
    	}
    }
    void Quick_sort(int* array,int len)
    {
    	 _sort(array,0,len-1);
    }
    
    void Print(int *array ,int len)
    {
    	for(int i = 0;i <len;i++)
    	{
    		cout<<array[i]<<endl;
    	}
    }
    
    int main()
    {
    	int array[]={6,7,5,4,3,9,1,2,0,8};
    	//char array[]="dcbazyxqpo";
    	int len =sizeof(array)/sizeof(array[0]);
    
    	Quick_sort(array,len);
    	Print(array,len);
    	return 0;
    }

**（4）结果展示**  
![这里写图片描述][70 11]  
\#\#\#【6】归并排序  
**（1）算法思想**  
在待排序的数据中，先将其划分为若干个有序的小序列，再将这每个小序列合并成大序列，以此往复；

**（2）算法示意图**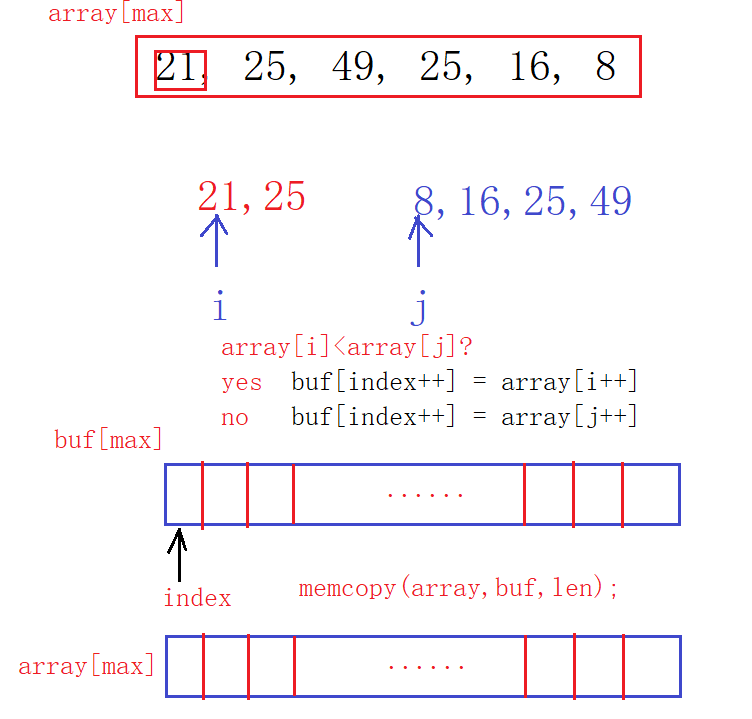  
![这里写图片描述][70 12]  
**（3）程序代码**

#include <stdio.h>
    #include <malloc.h>
    
    void printArray06(int array[], int len)
    {
    	int i = 0;
    	for(i=0; i<len; i++)
    	{
    		printf("%d ", array[i]);
    	}
    	printf("\n");
    }
    
    void swap6(int array[], int i, int j)
    {
    	int temp = array[i];
    	array[i] = array[j];
    	array[j] = temp;
    }
    
    void Merge(int src[], int des[], int low, int mid, int high)
    {
    	int i = low;
    	int j = mid + 1;
    	int k = low;
    
    	while( (i <= mid) && (j <= high) ) //将小的放到目的地中
    	{
    		if( src[i] < src[j] )
    		{
    			des[k++] = src[i++];
    		}
    		else
    		{
    			des[k++] = src[j++];
    		}
    	}
    
    	while( i <= mid )  //若还剩几个尾部元素
    	{
    		des[k++] = src[i++];
    	}
    
    	while( j <= high ) //若还剩几个尾部元素
    	{
    		des[k++] = src[j++];
    	}
    }
    
    //每次分为两路 当只剩下一个元素时，就不需要在划分
    void MSort(int src[], int des[], int low, int high, int max)
    {
    	if( low == high ) //只有一个元素，不需要归并，结果赋给des[low]
    	{
    		des[low] = src[low]; 
    	}
    	else //如果多个元素，进行两路划分
    	{
    		int mid = (low + high) / 2;
    		int* space = (int*)malloc(sizeof(int) * max);
    
    		//递归进行两路，两路的划分 
    		//当剩下一个元素的时，递归划分结束，然后开始merge归并操作
    		if( space != NULL )
    		{
    			MSort(src, space, low, mid, max); 
    			MSort(src, space, mid+1, high, max);
    			Merge(space, des, low, mid, high); //调用归并函数进行归并
    		}
    
    		free(space);
    	}
    }
    
    void MergeSort(int array[], int len) // O(n*logn)
    {
    	MSort(array, array, 0, len-1, len);
    }
    
    int main()
    {
    	int array[] = {21, 25, 49, 25, 16, 8};
    	int len = sizeof(array) / sizeof(*array); 
    	printArray06(array, len);
    	MergeSort(array, len);
    	printArray06(array, len);
    	return 0;
    }

**（4）结果展示**  
![这里写图片描述][70 13]

\#\#\#【7】堆排序  
**（1）算法思想**  
顾名思义，堆排序是利用大堆小堆来进行排序，使用向上调整以及向下调整的方法进行排序；分为两个大的部分：  
（1）、建堆  
（2）、排序  
**（2）程序代码**

#include<iostream>
    using namespace std;
    #define SIZE 10
    
    void create_heap(int *array,int n, int parent)
    {
    	int root;
    	int end;
    	int right;
    
    	root = array[parent];
    	end = parent;
    	right = 2*end +1;
    
    	while(right < n)
    	{
    		if( right<n-1  &&array[right]<array[right+1])
    		{
    			right++;
    		}
    
    		if(root<array[right])
    		{
    			array[end] = array[right];
    			end = right;
    			right = 2*end+1;
    		}
    		else{
    			break;
    		}
    	}
    	array[end] = root;
    }
    
    void Heap_Sort(int *array,int n)
    {
    	int i,end,key;
    	int *root;
    	for(i = n/2-1;i>=0;i++)
    	{
    		create_heap(array,n,i);
    	}
    
    	for(end = n-1;end>=1;end--)
    	{
    		key=array[0];
    		array[0] = array[end];
    		array[end] = key;
    
    		create_heap(array,end,0);
    	}
    }
    
    void Print(int *array)
    {
    	for(int i = 0; i<SIZE;i++)
    	{
    		cout<<array[i]<<" ,";
    	}
    
    }
    int main()
    {
    	int array[SIZE]={2,5,4,9,3,6,8,7,1,0};
    	int len = sizeof(array)/sizeof(array[0]);
    
    	Heap_Sort(array,len);
    	cout<<"堆排序结果为："<<endl;
    	Print(array);
    
    	return 0;
    }

**（3）结果展示**  
![这里写图片描述][70 14]

## 五、排序算法的比较 ##

**（1）稳定性比较**

*  插入排序、冒泡排序、归并排序、以及其他线性排序是稳定的；
 *  选择排序、希尔排序、快速排序、堆排序是不稳定的；

**（2）时间复杂度的比较**

*  \*\*O(n^2)\*\*插入排序，冒泡排序、选择排序
 *  \*\*O(nlog2n)\*\*堆排序，最优的快速排序

**（3）辅助空间比较**  
归并排序为O(n)，其余为O(1)

[70]: /images/20220522/7757d1c97850446b92dc82e45870bf36.png
[70 1]: /images/20220522/9d969796430f4f58b3c05ca3d6511b87.png
[70 2]: /images/20220522/ae6b4e51f6e542b0816c5b67b252ea81.png
[70 3]: /images/20220522/e3168ad489ce4d13b3ac99c63e47069e.png
[70 4]: /images/20220522/9f596ae3f4694be28d1e34d3dc2b0719.png
[70 5]: /images/20220522/c7010b25731749e388fcb929f42e00ae.png
[70 6]: /images/20220522/9a82174a914c41eaac72d308a2802cab.png
[70 7]: /images/20220522/06a699183afe4f3f960e97a0125a9b7c.png
[70 8]: /images/20220522/8a575e12492f4c85a1b3744257e858e5.png
[70 9]: /images/20220522/1d6daecb7d2749208bce5b72233c3e44.png
[70 10]: /images/20220522/d671d43df7b34e82b498f7c764a2cc03.png
[70 11]: /images/20220522/7adc497f494c46e58ed9a49493865321.png
[70 12]: /images/20220522/11da7543e9ca425eb6a0d60b67e4c97a.png
[70 13]: /images/20220522/48ae2c55105f46b8b50548717236da57.png
[70 14]: /images/20220522/12090e2b8943429a93089d8d0bfab507.png