二叉树的先序遍历,中序遍历,后序遍历和层序遍历
1.二叉树的构成
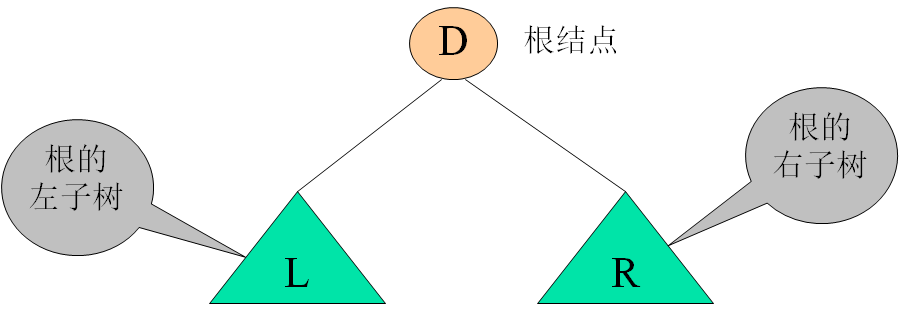
任何一个非空的二叉树都由根结点、左子树、右子树这三部分构成。
树的遍历是访问树中每个结点仅一次的过程。可将遍历看作是把所有的结点放在一条线上(即对树进行线性化的处理)。
2.二叉树的遍历
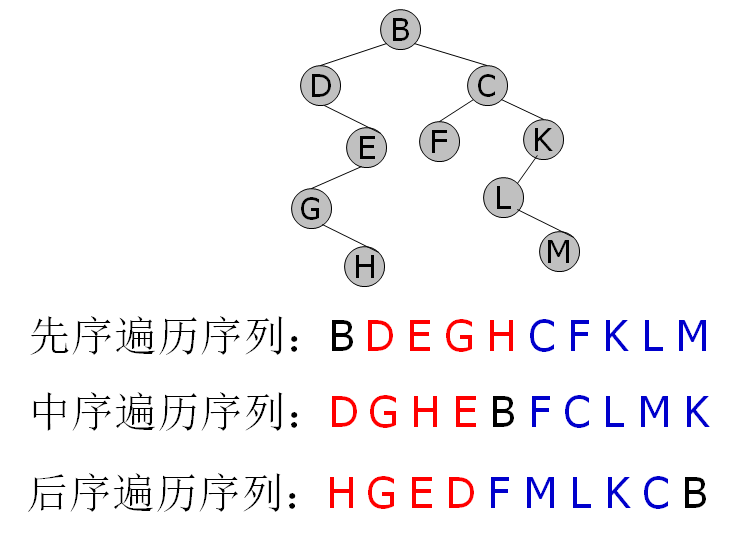
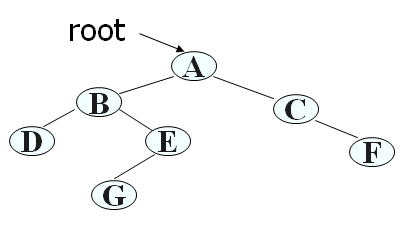
先序遍历: DLR 中序遍历:LDR 后序遍历:LRD 层序遍历:一层一层从左向右依次输出
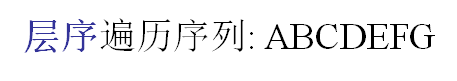
3.实现代码:
先序遍历采用递归的方式:
- 若二叉树非空
- (1)访问根结点;
- (2)先序遍历左子树;
- (3)先序遍历右子树
//先序遍历Status PreOrderTraverse(BiTree T){if(T){visit(T);PreOrderTraverse(T->lchild);PreOrderTraverse(T->rchild);}return ok;}
中序遍历:
- 若二叉树非空
- (1)中序遍历左子树;
- (2)访问根结点;
- (3)中序遍历右子树;
//中序遍历Status InOrderTraverse(BiTree T){if(T){InOrderTraverse(T->lchild );visit(T);InOrderTraverse(T->rchild );}return ok;}
后序遍历:
- 若二叉树非空
- (1)后序遍历左子树
- (2)后序遍历右子树
- (3)访问根结点D
//后序遍历Status PostOrderTraverse(BiTree T){if(T){PostOrderTraverse(T->lchild );PostOrderTraverse(T->rchild );visit(T);}return ok;}
层序遍历:
n先根,后子树;先左子树,后右子树。
利用队列实现二叉树的层序遍历:
- 构造一个空队列;
- 树根结点入队列;
- while (队列不空) {
- 令队头结点X出队列;
- 访问结点X;
- 若X的左孩子、右孩子结点存在,则依次加入队列;
- }
//层序遍历Status levelOrder(BiTree T){LinkQuene Q;BiTree A;InitQuene( Q);EnQuene(Q,T);while(!EmptyQue(Q)){A=Q.front->next->data;visit(A);if(A->lchild!=NULL)EnQuene(Q,A->lchild);if(A->rchild!=NULL)EnQuene(Q,A->rchild);DeQuene(Q);}
4.二叉树的存储结构:
typedef struct BiNode{
TElemType data;
struct BiNode *lchild,*rchild;
}BiNode,*BiTree;
5.创建二叉树:
Status CreateBiTree(BiTree &T){char ch;scanf("%c",&ch);if(ch=='.') T=NULL;else{T=(BiTree)malloc(sizeof(BiNode));if(!T) exit(overflow);T->data=ch;CreateBiTree(T->lchild);CreateBiTree(T->rchild);}return ok;}
6.测试代码—主函数
int main(){BiTree T;printf("以先序遍历序列输入创建二叉树:\n");CreateBiTree(T);printf("依次输出先序,中序,后序及层序遍历序列:\n") ;PreOrderTraverse(T);printf("\n");InOrderTraverse(T);printf("\n");PostOrderTraverse(T);printf("\n");levelOrder(T);printf("\n");system("pause");return 0;}
7.当然,对于层序遍历中的有关队列的一些基本函数没有细化,故在此将完整代码写出供大家参考:
#include<stdio.h>#include<stdlib.h>#include<malloc.h>#define ok 1#define error 0#define true 1#define false 0#define overflow -2typedef int Status;typedef char TElemType;//定义二叉树结构typedef struct BiNode{TElemType data;struct BiNode *lchild,*rchild;}BiNode,*BiTree;//打印函数void visit(BiTree p){printf("%c ",p->data);}//队列结构,用于层序遍历typedef BiTree QElemType;typedef struct QNode{QElemType data;struct QNode *next;}QNode,*QuenePtr;typedef struct {QuenePtr front;QuenePtr rear;}LinkQuene;//初始化队列Status InitQuene(LinkQuene &Q){Q.front=Q.rear=(QuenePtr)malloc(sizeof(QNode));if(!Q.front)exit(overflow);Q.front->next=NULL;return ok;}//判断队列是否为空Status EmptyQue(LinkQuene Q){if(Q.front==Q.rear)return true;elsereturn false;}//入队Status EnQuene(LinkQuene &Q,QElemType e){QuenePtr p;p=(QuenePtr)malloc(sizeof(QNode));if(!p)exit(overflow);p->data=e;p->next=NULL;Q.rear->next=p;Q.rear=p;return ok;}//出队Status DeQuene(LinkQuene &Q){QuenePtr p;if(Q.front==Q.rear)return error;p=Q.front->next;Q.front->next=p->next;if(Q.rear==p)Q.rear=Q.front;free(p);return ok;}//创建二叉树Status CreateBiTree(BiTree &T){char ch;scanf("%c",&ch);if(ch=='.') T=NULL;else{T=(BiTree)malloc(sizeof(BiNode));if(!T) exit(overflow);T->data=ch;CreateBiTree(T->lchild);CreateBiTree(T->rchild);}return ok;}//先序遍历Status PreOrderTraverse(BiTree T){if(T){visit(T);PreOrderTraverse(T->lchild);PreOrderTraverse(T->rchild);}return ok;}//中序遍历Status InOrderTraverse(BiTree T){if(T){InOrderTraverse(T->lchild );visit(T);InOrderTraverse(T->rchild );}return ok;}//后序遍历Status PostOrderTraverse(BiTree T){if(T){PostOrderTraverse(T->lchild );PostOrderTraverse(T->rchild );visit(T);}return ok;}//层序遍历Status levelOrder(BiTree T){LinkQuene Q;BiTree A;InitQuene( Q);EnQuene(Q,T);while(!EmptyQue(Q)){A=Q.front->next->data;visit(A);if(A->lchild!=NULL)EnQuene(Q,A->lchild);if(A->rchild!=NULL)EnQuene(Q,A->rchild);DeQuene(Q);}return ok;}int main(){BiTree T;printf("以先序遍历序列输入创建二叉树:\n");CreateBiTree(T);printf("依次输出先序,中序,后序及层序遍历序列:\n") ;PreOrderTraverse(T);printf("\n");InOrderTraverse(T);printf("\n");PostOrderTraverse(T);printf("\n");levelOrder(T);printf("\n");system("pause");return 0;}
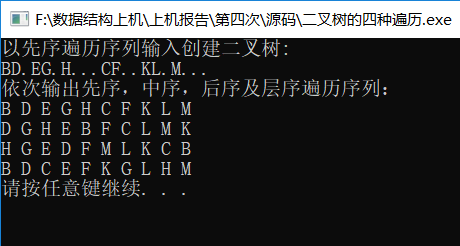
8.程序截图
此范例既是上面所举例子,可自行核对。





























还没有评论,来说两句吧...