数据结构与算法习题部分：动态规划、贪婪算法-蒲公英云

数据结构与算法习题部分：动态规划、贪婪算法

朱雀 2022-01-31 23:19 331阅读 0赞

一、动态规划
定义：动态规划是指如果我们要求一个问题的最优解，而且该问题可以分解成若干个子问题，并且问题之间还有重叠的更小的子问题，我们就可以考虑用动态规划去解决这个问题。
解决动态规划的问题有四个特点：
1、我们在应用动态规划之前要分析能否把大问题分解成小问题，如果分解的每个小问题也存在最优解，那么把这些小问题的最优解组合起来就能够得出这个问题的最优解，我们就可以应用动态规划解决这个问题
2、整体问题的最优解是依赖于子问题的最优解
3、大问题分解成小问题以后，这些小问题之间还有相互重叠的小问题
4、为避免重复求解子问题，我们可以自上而下分析问题，自下而上求解问题
（动态规划的本质就是自下而上求解问题）
最优子结构：
通过求解子问题的最优解，可以获得原问题的最优解
我们在动态规划运用递归时还要注意，其中是否有重叠子问题和最优子结构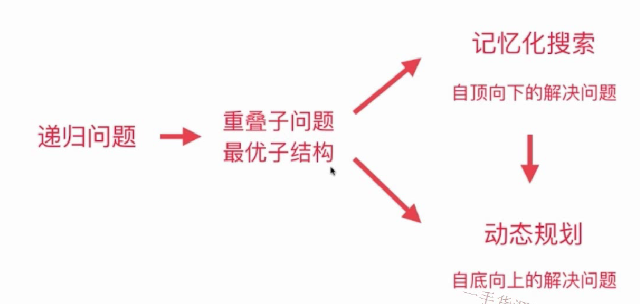
在这里插入图片描述
现在添加一个2000美元的手机，背包还是4磅，计算出最优解
基本题目如下：
有4样商品，分别是
（1）音响：4磅：3000美元
（2）笔记本电脑：3磅：2000美元
（3）iphone:1磅：2000 美元
（4）吉他：1磅：1500美元
只有一个4磅的背包，如何使商品价值最大
下面是代码行：

#背包问题
    import numpy as np
    price=[3000,2000,2000,1500] #价格
    weight=[4,3,1,1] #对应的重量
    m=4 #背包重量
    n=4 #物品数
    x=np.zeros([n+1,m+1])
    for i in range(1,n+1):
        for j in range(1,m+1):
            if weight[i-1]<=j:
                x[i][j]=max(x[i-1][j],x[i-1][j-weight[i-1]]+price[i-1])
            else:
                x[i][j]=x[i-1][j]        
    print(x)    
    res=x
    def show(n,m,w,res):
        print('最大价值为:',res[n][m])
        item=[False for i in range(n)]
        j=m
        for i in range(n,0,-1):
            if res[i][j]>res[i-1][j]: #代表取了这件物品
                item[i]=True
                j=j-weight[i]
        for i in range(n):
            if item[i]:
                print('第',i,'个,',end='')
    show(n,m,weight,res)

结果：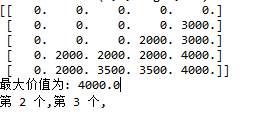
在这里插入图片描述
例题2：走网格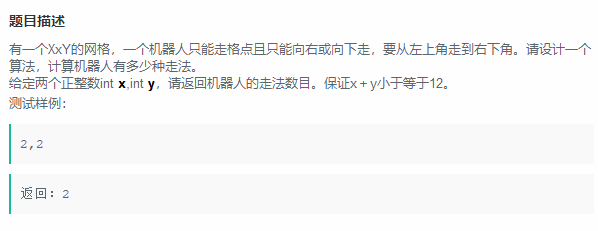

import numpy as np
    class Robot:
        def countWays(self, x, y):
            if x == 1 or y == 1:
                return 1
            else:
                dp = np.ones((x,y))
                for i in range(1,x):
                    for j in range(1,y):
                           dp[i][j]=dp[i][j-1]+dp[i-1][j]
            return int(dp[-1][-1])

习题1：减绳子
剑指offer习题14
给你一根长度为n的绳子，请把绳子剪成m段 (m和n都是整数，n>1并且m>1)每段绳子的长度记为k[0],k[1],…,k[m]。请问k[0]k[1]…*k[m]可能的最大乘积是多少？例如，当绳子的长度为8时，我们把它剪成长度分别为2,3,3的三段，此时得到的最大乘积是18。m是未知的，我么只求分割的总的乘积最大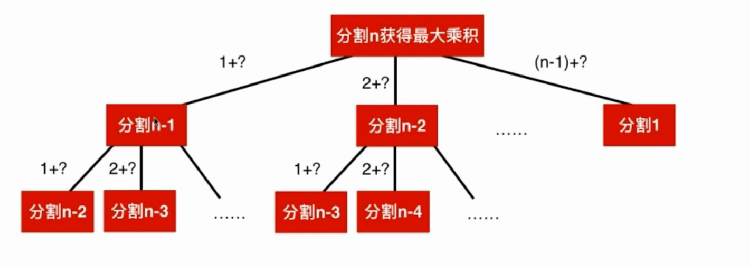
在这里插入图片描述

class solution:
    def __init__(self):
        self.res=-1
    def Integerbreak(self,n):
        return breakInteger(n)
    def max3(self,a,b,c):
        return (max(a,max(b,c)))
    # 将n进行分割，至少分割两部分，可以获得的最大的乘积
    def breakInteger(self,n):
        if n==1:
            return 1
        #这里的res是多个值中选取最大值的比较方法，我们比如我们要比较a,b,c,我们可以找一个中介变量
        #遍历一遍a,b,c，每次将值和res比较，将较大的值给res,最后遍历完res便是最大值
        res=-1
        for i in range(1,n):
            res=self.max3(res,i*(n-i),i*self.breakInteger(n-i))
        return res
print(solution().max3(1,2,3))
print(solution().breakInteger(8))
def max_n(List):
    res=-1
    for i in List:
        res=max(res,i)
    return res
print(max_n([1,2,4,3,2,3,4]))

补充习题，求一个数分割的组合数
比如10可以分割成哪几个数的组合，有（1，9），（2，8），（3，2，2，3）等等

class solution1:
    def max_spilt(self,n):
        self.dic = {
    i:None for i in range(1,n+1)}
        #print(self.dic)
        return self.max_count_mixnum(n)
    #将n进行最少分割两次的组合数的集合
    def max_count_mixnum(self,n):
        a=False
        if n==1:
            return [[1]]
        arr1=[]
        for i in range(1,n):
            if self.dic[n-i] is not None:
                a=True
                res=self.dic[n-i]
            else:
                res=self.max_count_mixnum(n-i)
            for j in res:
                j.append(i)
                arr1.append(j)
        if a:
            self.dic[n-i]=arr1
        return arr1