选择排序之堆排序（HeapSort）-蒲公英云

选择排序之堆排序（HeapSort）

图解排序算法(三)之堆排序

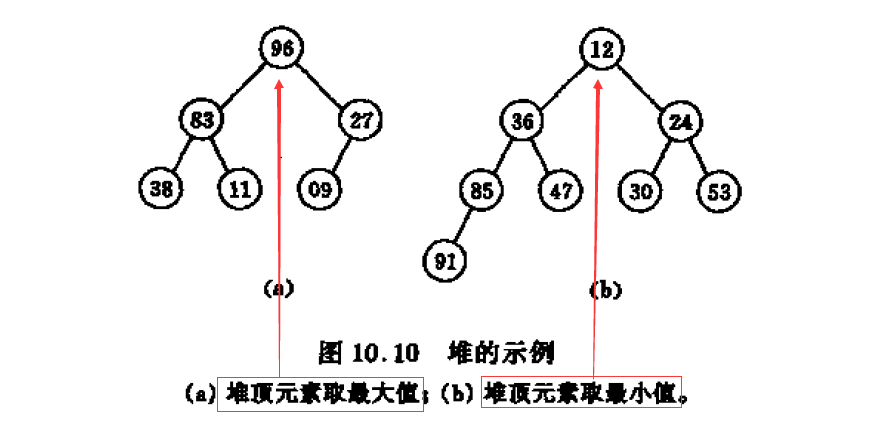
一、堆定义

（二叉）堆是一个数组，类似于完全二叉树。分为两种形式：
这里写图片描述

二、维持堆性质

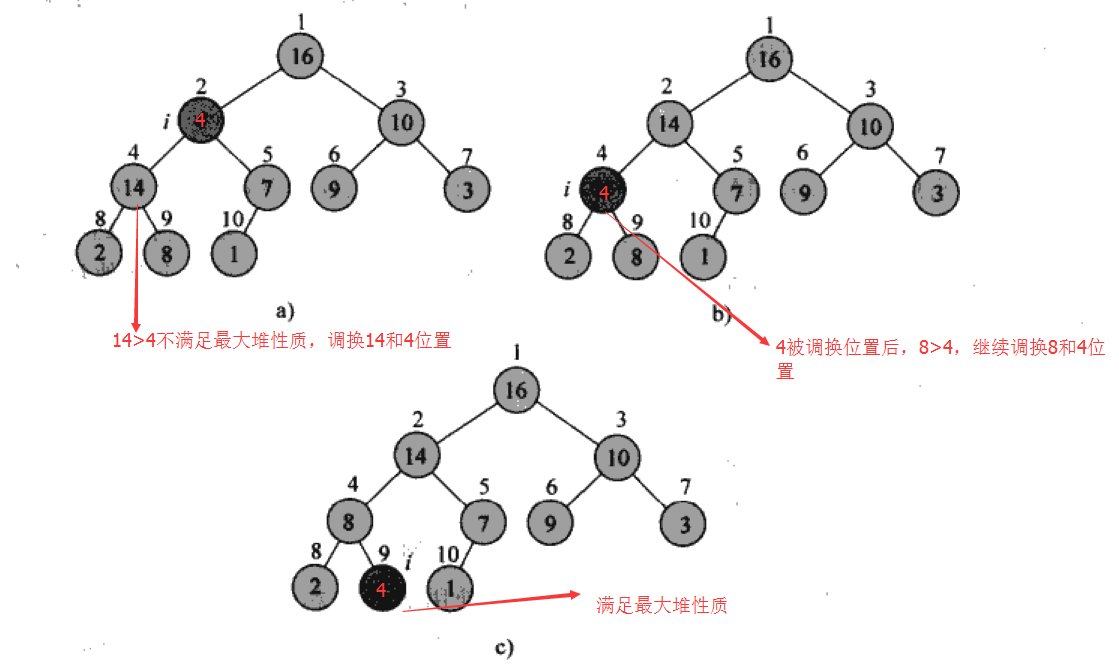
堆排序使用的是最大堆，如果堆中某个结点不满足最大堆性质，这时就需要用算法调整节点位置，使得满足最大堆性质。
这里写图片描述

三、建堆

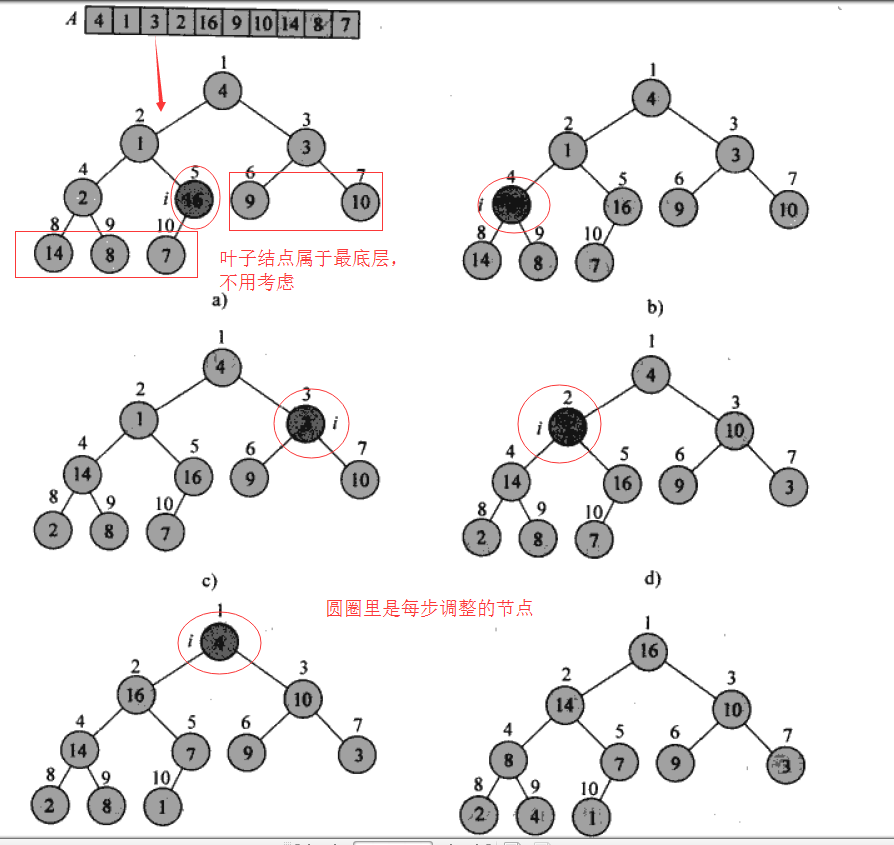
默认数组为一个无序堆，通过数组前部分数组调用MAX-HEAPIFY函数来调整节点来使其满足最大堆性质。
这里写图片描述

四、堆排序

由于堆已经排好序，我们只需要逐渐取出节点就可以完成排序。堆排序对于记录数较少文件并不提倡。但对于n较大文件还是很有效。但是其运行时间主要消耗在建初始堆和调整新堆上。
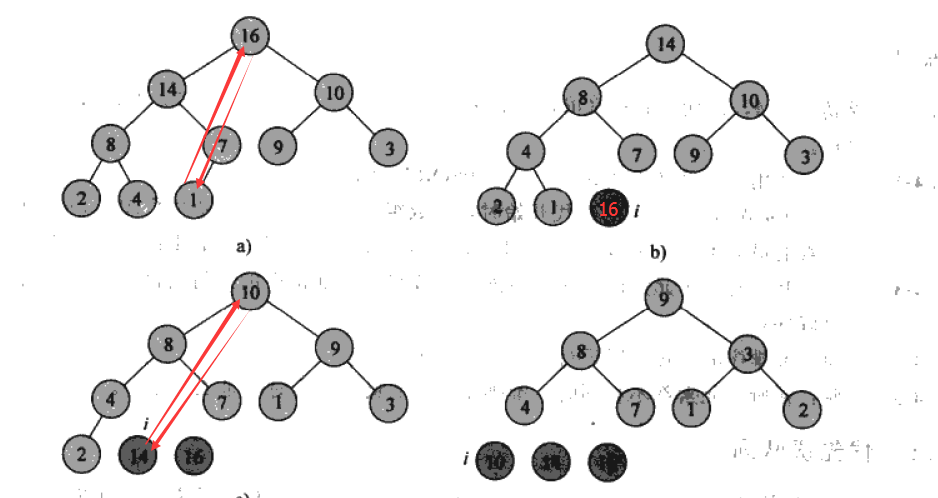
这里写图片描述

1、建堆：从倒数第一个非叶子节点开始，逐个比较节点和其左右儿子节点的大小，如果将父节点和子节点交换，那么就需要再次验证交换后的子节点是否满足要求。
2、排序：从最后一个节点开始，逐个将节点和堆顶节点交换，这样就能把最大值一直拿出来。

//实现
public class Main{
    public static void main(String[] args){
        int[] a = {1,5,3,7,5,2,-1,6};
        heapSort(a);
        for(int i=0; i<a.length; i++)
            System.out.println(a[i]);
    }
    private static void heapSort(int[] a){
        buildHeap(a);
        for(int i=a.length-1; i>0; i--){   //从a.length-1到1逐渐交换，最优剩的0位置不用再排
            swap(a, i, 0);
            heapify(a, 0, i);   //注意这个地方size一直在变化以避免再次将最大值加入堆中。
        }
    }
    private static void buildHeap(int[] a){
        int size = a.length;
        for(int i = (size-2)/2; i>=0; i--){   //从倒数第一个非叶子节点调整
            heapify(a, i, size);
        }
    }
    private static void heapify(int[] a, int i, int size){
        int left = 2*i+1;
        int right = 2*i+2;
        int largest = i;
        if(left<size && a[left]>a[largest]){
            largest = left;
        }
        if(right<size && a[right]>a[largest]){
            largest = right;
        }
        if(largest!=i){
            swap(a, largest, i);
            heapify(a, largest, size);
        }
    }
    private static void swap(int[] a, int i, int j){
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}