隐式类型转换

布满荆棘的人生 2023-10-04 23:37 115阅读 0赞

文章目录

  • 前言
    • 整形提升的概念
    • 整形提升的意义
    • 如何进行整形提升
      • 例一
      • 例二
      • 例三
  • 总结

前言

  我们在编程中经常进行数值运算，那么你清楚它具体是怎么进行的吗？本期就来带大家深入了解一下计算机进行数值运算的方法。

整形提升的概念

  C的整型算术运算总是至少以缺省整型类型的精度来进行的。为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。
  这个的意思就是在使用char和short类型时会先进行整形提升，也就是从使用1个字节（char)变成使用4个字节，运算完成之后再进行截断，char只截取一个字节，short截取两个字节。

  1. char a = 256;
  2.     //0000 0000 0000 0000 0000 0001 0000 0000  一个字节8个bit位
  3.     //截断:0000 0000
  4.     char b = 257;
  5.     //0000 0000 0000 0000 0000 0001 0000 0001
  6.     //截断:0000 0001
  7.     printf("%d\n", a);
  8.     printf("%d\n", b);
  9.     return 0;

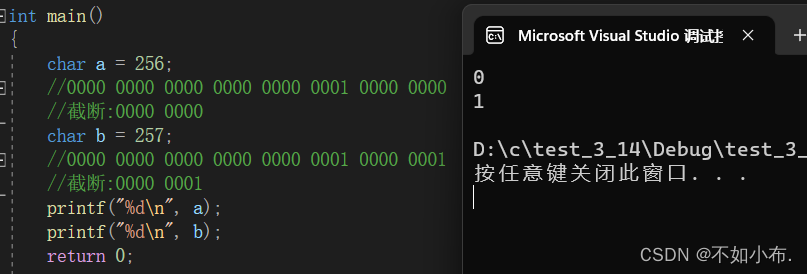
在这里插入图片描述

整形提升的意义

  表达式的整型运算要在CPU的相应运算器件内执行，CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度，同时也是CPU的通用寄存器的长度。
  因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。
  通用CPU（general-purpose CPU）是难以直接实现两个8比特字节直接相加运算（虽然机器指令中可能有这种字节相加指令）。所以，表达式中各种长度可能小于int长度的整型值，都必须先转换为int或unsigned int，然后才能送入CPU去执行运算。

如何进行整形提升

  整形提升是按照变量的数据类型的符号位来提升的。

  1. //负数的整形提升
  2. char c1 = -1;
  3. 变量c1的二进制位(补码)中只有8个bit位：
  4. 1111111
  5. 因为 char 为有符号的 char
  6. 所以整形提升的时候，高位补充符号位，即为1
  7. 提升之后的结果是：
  8. 11111111111111111111111111111111
  9. //正数的整形提升
  10. char c2 = 1;
  11. 变量c2的二进制位(补码)中只有8个bit位：
  12. 00000001
  13. 因为 char 为有符号的 char
  14. 所以整形提升的时候，高位补充符号位，即为0
  15. 提升之后的结果是：
  16. 00000000000000000000000000000001
  17. //无符号整形提升，高位补0

例一

  1. char a = 3;
  2.     //0000 0000 0000 0000 0000 0000 0000 0011
  3.     //0000 0011 发生截断
  5.     char b = 127;
  6.     //0000 0000 0000 0000 0000 0000 0111 1111
  7.     //0011 1111 截断
  9.     char c = a + b;
  10.     //先将 a 整形提升:0000 0000 0000 0000 0000 0000 0000 0011
  11.     //再将 b 整形提升:0000 0000 0000 0000 0000 0000 0111 1111
  13.     //c 的值:0000 0000 0000 0000 0000 0000 1000 0010
  14.     //发生截断:1000 0010
  15.     //整形提升:1111 1111 1111 1111 1111 1111 1000 0010 
  16.     printf("%d", c);
  17.     //这里是由%d打印，其实就是将c看成了整型
  18.     //1111 1111 1111 1111 1111 1111 1000 0010 补码
  19.     //1000 0000 0000 0000 0000 0000 0111 1101 反码
  20.     //1000 0000 0000 0000 0000 0000 0111 1100 原码
  21.     //-126

例二

  1. char a = 0xb6;
  2.  short b = 0xb600;
  3.  int c = 0xb6000000;
  4.  if(a == 0xb6)
  5.  {
  7.      printf("a");
  8.  }
  9.  if(b == 0xb600)
  10.  {
  12.      printf("b");
  13.  }
  14.  if(c == 0xb6000000)
  15.  {
  17.      printf("c");
  18.  }
  19.  return 0;

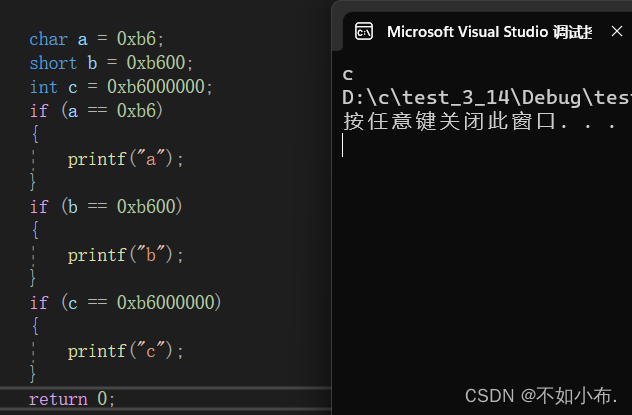
在这里插入图片描述
  这里的0xb6转化为二进制就是 1011 0110，按照前面整形提升的方法，这是有符号char，前面补符号位，也就是1，结果就是1111 1111 1111 1111 1111 1111 1011 0110，在内存中存储的是补码，要转化为原码来看。

  1. 1111 1111 1111 1111 1111 1111 1011 0110 //补码
  2. 1000 0000 0000 0000 0000 0000 0100 1001 //反码，符号位不变，其余按位取反
  3. 1000 0000 0000 0000 0000 0000 0100 1000 //原码，反码-1
  • 0xb6换成二进制就是
    0000 0000 0000 0000 0000 0000 1011 0110 // 182
  • a的实际存储是
    1000 0000 0000 0000 0000 0000 0100 1000 // -74
  • 两者的数据是不一样的，short同理，只有c是整型，不会发生整型提升，所以最终相等。

例三

  1. char c = 1;
  2.     char d = 2;
  3.     printf("%u\n", sizeof(c));
  4.     printf("%u\n", sizeof(c+d));
  5.     return 0;

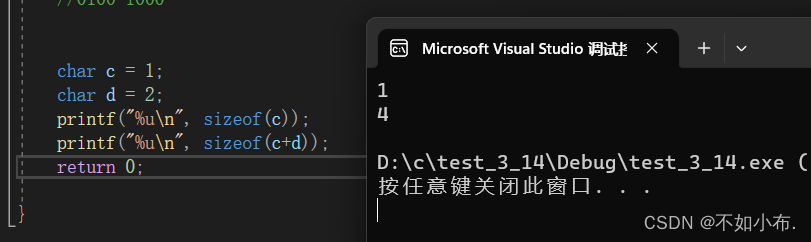
在这里插入图片描述

  • 原因是只要参加了表达式运算，就会发生整型提升，这也是一个证明整型提升的例子。

总结

  因为对这部分内容不太常用，而且我也不太熟悉，所以迟迟未写，恰好今天有空，就去补了一下前面的内容，顺便写出来巩固自己的理解。
  谢谢大家观看，如果有什么不懂的地方可以私信或者评论区留言嗷，觉得不错可以点赞加收藏哦。学习时光阴总是流逝的飞快，那么本期就到此结束，让我们下期再见。

发表评论

表情：
评论列表 （有 0 条评论，115人围观）

还没有评论，来说两句吧...

相关阅读

    相关 隐式类类型转换

    C++ primer 中有这么一句话：可以用单个实参来调用的构造函数定义了从形参类型到该类型的一个隐式转换。 这么解释： 比如有个类A的对象a的成员函数的参数应该是类A的对

    ゝ一世哀愁。ゝ一世哀愁。/ 0 赞/ 335 阅读