C语言：猜数字游戏——给“余”猜数

红太狼 2023-07-17 04:47 2阅读 0赞

## 猜数字游戏——给“余”猜数游戏 ##

**问题概述：**  
你心里先想好一个1~100之间的整数x，将它分别除以3、5和7并得到三个余数。你把这三个余数告诉计算机，计算机能马上猜出你心中的这个数。

**游戏过程：**  
Please think of a number between 1 and 100  
Your number divided by 3 has a remainder of?  
Your number divided by 5 has a remainder of?  
Your number divided by 7 has a remainder of?  
Let think a moment,emmm–  
Oh,your number was\*\*\*

**问题分析：**

1.  算法的关键：找出余数与求解数之间的关系，建立问题的数学模型；
2.  数学模型:  
    （1）不难理解当s=u+3*v+3*w时，s除以3的余数与u除以3的余数相同;  
    （2）对s=cu+3*v+3*w，当c除以3余数为1的数时, s除以3的余数与u除以3的余数相同。
3.  证明如下：  
    c 除以3余数为1，记c=3*k+1，则s=u+3*k*u+3*v+3*w，由1)的结论，上述结论正确。 记a，b，c分别为所猜数据d除以3，5，7后的余数，则d=70*a+21*b+15*c为问题的数学模型，其中70称作a的系数，21称作b的系数,15称作c的系数。
4.  问题总结：  
    （1） b、c的系数能被3整除，且a的系数被3整除余1；这样d除以3的余数与a相同；  
    （2）a、c的系数能被5整除，且b的系数被5整除余1；这样d除以5的余数与b相同；  
    （3）a、b的系数能被7整除，且c的系数被7整除余1；这样d除以7的余数与c相同。  
    **由此可见：**  
    c的系数是3和5的最公倍数且被7整除余1，正好是15；  
    a的系数是7和5的最公倍数且被3整除余1，最小只能是70；  
    b的系数是7和3的最公倍数且被5整除余1，正好是21。

**代码示例：**

#include<stdio.h> 
    #include <stdlib.h>
    int main( )
    { 
       int a,b,c,d;
       printf("Please think of a number between 1 and 100.\n");
       printf("your number divided by 3 has a reminder of:");
       scanf("%d",&a);
       printf("Your number divided by 5 has a reminder of:");
       scanf("%d",&b);
       printf("Your number divided by 7 has a reminder of:");
       scanf("%d",&c);
       printf("Let think a moment,emmm--");
       d=70*a+21*b+15*c;
       while(d>105)
        d=d-105;
       printf("Oh,your number was %d\n",d);
    }

**运行示例：**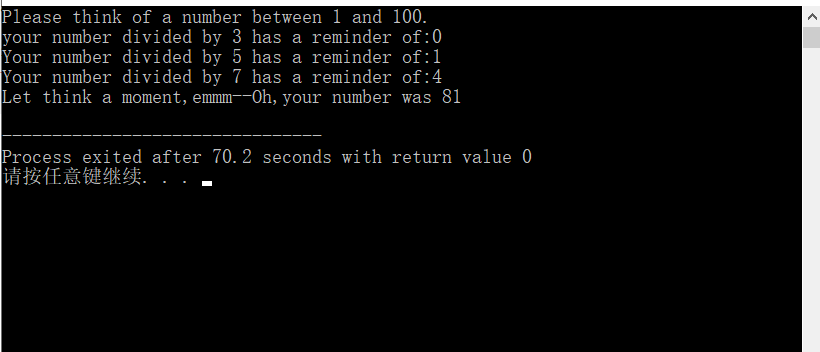  
![watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDE3MDQyMA_size_16_color_FFFFFF_t_70][]

[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDE3MDQyMA_size_16_color_FFFFFF_t_70]: /images/20230528/84587243906b4de0a4c1f8319c331690.png