中序线索化二叉树

1.头文件及类型定义
2.线索二叉树结点类型定义
3.函数声明
4.基本操作
- 4.1 先序建立线索二叉树
- 4.2 初始化tag
- 4.3 中序线索化二叉树
- - 4.3.1 访问并建立线索
  - 4.3.2 遍历
  - 4.3.3 中序线索化主过程
- 4.4 寻找中序后继
- - 4.4.1 找到最左下结点
  - 4.4.2 找到p的后继结点
- 4.4 寻找中序前驱
- - 4.4.1 找到最右下结点
  - 4.4.2 找到p的前驱
- 4.5 中序遍历和逆向中序遍历
- - 4.5.1 打印结点
  - 4.5.2 利用中序后继实现中序遍历
  - 4.5.3 利用中序前驱实现逆向中序遍历
- 4.6 main函数
- 4.7 测试
- - 4.7.1 二叉树结构
  - 4.7.2 测试结果
5.小结

1.头文件及类型定义

#include<stdio.h>
#include<stdlib.h>
#define ElemType char

2.线索二叉树结点类型定义

//线索二叉树结点类型定义
typedef struct ThreadNode {
    ElemType data;                            //数据元素
    struct ThreadNode* lchild, * rchild;    //左、右孩子指针
    int ltag, rtag;                            //左、右线索标志
    //tag=0,表示指针指向孩子;tag=1,表示指针是“线索”,ltag指向前驱，rtag指向后继
}ThreadNode, * ThreadTree;

3.函数声明

/*函数声明*/
void CreateThTree(ThreadTree& T);            //1.先序建立线索二叉树
void InitThread(ThreadTree& T);                //2.初始化tag
void visit1(ThreadNode* q);                    //3-1.访问并建立线索
void InThread(ThreadTree T);                //3-2.遍历
void CreateInThread(ThreadTree T);            //3-3.中序线索化主过程
ThreadNode* FirstNode(ThreadNode* p);        //4-1.找到以p为根的子树中，第一个被中序遍历的结点
ThreadNode* NextNode(ThreadNode* p);        //4-2.找到p的后继结点
ThreadNode* LastNode(ThreadNode* p);        //5-1.找到以p为根的子树中，最后一个被中序遍历的结点
ThreadNode* PreNode(ThreadNode* p);            //5-2.找到p的前驱结点    
void visit2(ThreadNode* p);                    //6-1.打印结点
void InOrder(ThreadNode* T);                //6-2.利用中序后继实现中序遍历
void RevInOrder(ThreadNode* T);                //6-3.利用中序前驱实现逆向中序遍历

4.基本操作

4.1 先序建立线索二叉树

/*1.先序建立线索二叉树*/
void CreateThTree(ThreadTree& T) {
    char c;
    scanf("%c", &c);
    if (c == '#')
        T = NULL;
    else {
        T = (ThreadNode*)malloc(sizeof(ThreadNode));
        T->data = c;
        CreateThTree(T->lchild);
        CreateThTree(T->rchild);
    }
}

4.2 初始化tag

/*2.初始化tag*/
void InitThread(ThreadTree& T) {
    if (T != NULL) {
        T->ltag = 0;
        T->rtag = 0;    //初始化当前树中的tag指针为0，表示还未线索化
        InitThread(T->lchild);    //递归遍历左子树
        InitThread(T->rchild);    //递归遍历右子树
    }
}

4.3 中序线索化二叉树

4.3.1 访问并建立线索

ThreadNode* pre = NULL;        //pre指向当前访问结点的前驱
//3-1.访问并建立线索
void visit1(ThreadNode* q) {
    if (q->lchild == NULL) {
        //左子树为空，建立前驱线索
        q->lchild = pre;
        q->ltag = 1;
    }
    if (pre != NULL && pre->rchild == NULL) {
        pre->rchild = q;    //建立前驱结点的后继线索
        pre->rtag = 1;
    }
    pre = q;            //标记当前结点为刚刚访问过的结点
}

4.3.2 遍历

//3-2.遍历
void InThread(ThreadTree T) {
    if (T != NULL) {
        InThread(T->lchild);    //中序遍历左子树
        visit1(T);                //访问根节点
        InThread(T->rchild);    //中序遍历右子树
    }
}

4.3.3 中序线索化主过程

//3-3.主过程
void CreateInThread(ThreadTree T) {
    pre = NULL;            //pre初始化为NULL
    if (T != NULL) {
        //非空二叉树才能线索化            
        InThread(T);    //中序线索化二叉树
        if (pre->rchild == NULL)    //实际上不用判断，中序遍历时最后一个结点的右孩子指针必为NULL
            pre->rtag = 1;            //处理遍历的最后一个结点
    }
}

4.4 寻找中序后继

4.4.1 找到最左下结点

//4-1.求中序线索二叉树中中序遍历的第一个结点：右子树中最左下的结点
ThreadNode* FirstNode(ThreadNode* p) {
    //循环找到最左下结点(不一定是叶节点)
    while (p->ltag == 0)
        p = p->lchild;
    return p;
}

4.4.2 找到p的后继结点

//4-2.找到p的后继结点
ThreadNode* NextNode(ThreadNode* p) {
    if (p->rtag == 0)        //若rtag=0，说明所找结点有右孩子，则找该结点的右子树最左下结点
        return FirstNode(p->rchild);
    else
        return p->rchild;    //若rtag=1，说明所找结点无右孩子，则返回后继线索
}

4.4 寻找中序前驱

4.4.1 找到最右下结点

//5-1.求中序线索二叉树中中序遍历的最后一个结点：左子树中最右下的结点
ThreadNode* LastNode(ThreadNode* p) {
    //循环找到最右下结点(不一定是叶节点)
    while (p->rtag == 0)
        p = p->rchild;
    return p;
}

4.4.2 找到p的前驱

//5-2.找到p的前驱结点
ThreadNode* PreNode(ThreadNode* p) {
    if (p->ltag == 0)        //若ltag=0，说明所找结点有左孩子，则找该结点的左子树最右下结点
        return LastNode(p->lchild);
    else
        return p->lchild;    //若ltag=1，说明所找结点无左孩子，则返回前驱线索
}

4.5 中序遍历和逆向中序遍历

4.5.1 打印结点

//6-1.打印结点
void visit2(ThreadNode* p) {
    printf("%c\t", p->data);
}

4.5.2 利用中序后继实现中序遍历

//6-2.利用中序后继实现中序遍历：空间复杂度为O(1) 
void InOrder(ThreadNode* T) {
    for (ThreadNode* p = FirstNode(T); p != NULL; p = NextNode(p))
        visit2(p);
}

4.5.3 利用中序前驱实现逆向中序遍历

//6-2.利用中序后继实现中序遍历：空间复杂度为O(1) 
void RevInOrder(ThreadNode* T) {
    for (ThreadNode* p = LastNode(T); p != NULL; p = PreNode(p))
        visit2(p);
}

4.6 main函数

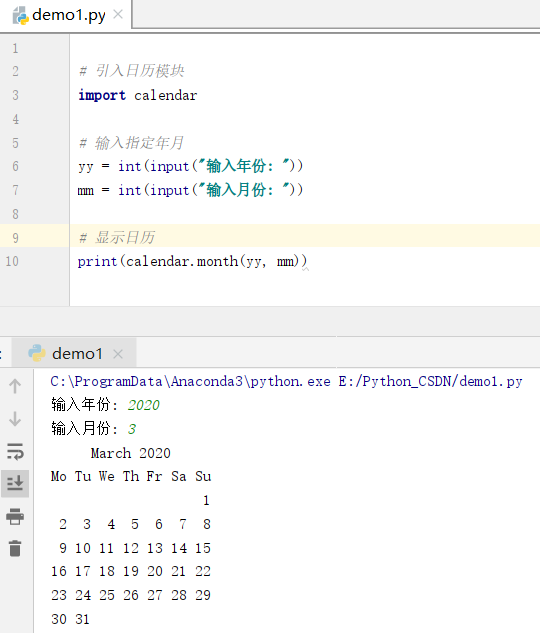
int main() {
    ThreadTree T;
    /*1、创建二叉树*/
    printf("先序创建二叉树：");
    CreateThTree(T);
    /*2、初始化tag为0*/
    InitThread(T);
    /*3、中序线索化*/
    CreateInThread(T);
    /*4、寻找中序后继（用根结点测试）*/
    printf("根结点的中序后继为：%c\n", NextNode(T)->data);
    /*5、寻找中序前驱（用根结点测试）*/
    printf("根结点的中序前驱为：%c\n", PreNode(T)->data);
    /*6、中序遍历二叉树*/
    printf("<————中序遍历————>\n");
    InOrder(T);
    /*7、逆向中序遍历二叉树*/
    printf("\n<————逆向中序遍历————>\n");
    RevInOrder(T);
    return 0;
}

4.7 测试

4.7.1 二叉树结构

在这里插入图片描述

4.7.2 测试结果

在这里插入图片描述

5.小结

关于线索二叉树
二叉树的线索化是将二叉链表中的n+1个空指针改为指向前驱或后继的线索。但前驱或后继的信息只有在遍历时才能得到，因此，线索化二叉树的本质是二叉树的遍历。
在对二叉树进行线索化以后，就可以很方便的找到指定结点的前驱或者后继，并且，利用寻找中序前驱或者中序后继的操作可以很方便的实现二叉树的中序遍历和逆向中序遍历，且这样实现的遍历空间复杂度仅为O(1)。