一文读懂特征值分解EVD与奇异值分解SVD

落日映苍穹つ 2023-02-25 15:28 3阅读 0赞

这篇关于特征值和特征向量的内容是我用PCA的时候接触到的，本科学的东西早就记不得了orz，所以复习了一遍顺便做了一下梳理，这算是PCA的前置知识。

# 特征值分解 #

## 特征值与特征向量 ##

设  A A A 是  n n n 阶矩阵, 如果数 λ \\lambda λ 和  n n n 维非零列向量  x x x 使关系式  
 A x = λ x A x=\\lambda x Ax=λx成立，那么 λ \\lambda λ 就称为矩阵  A A A 的特征值,  x x x 称为 A A A的对应于特征 值  λ \\lambda λ 的特征向量。

> 注意有两个要素：（1） A A A是方阵（2） x x x是非零向量

我们都知道左乘矩阵代表的是线性变换，上述定义从几何来理解就是：向量  x x x 经过 A A A变换后，它的方向没有变（可能会相反），而大小变为 λ \\lambda λ倍。这是一种很特殊的情况，你想变换后的向量形式千千万，唯独某类向量会保持住它的方向不变，而只改变其长度，这类向量对 A A A来说是及其特殊的存在，所以我们可以认为矩阵 A A A的特征可以由这些特征值和对应的特征向量所体现（这可能是“特征”两字的由来）。  
![2020060619500350.jpg_pic_center][]  
定义可以写成：  ( A − λ E ) x = 0 (A-\\lambda E) x=0 (A−λE)x=0这是一个齐次线性方程组，它有非零解的充分必要条件是系数行列式等于0，也就是 ∣ A − λ E ∣ = 0 |A-\\lambda E|=0 ∣A−λE∣=0这个式子化简以后是以  λ \\lambda λ 为未知数的一元  n n n 次方程，称为矩阵  A A A 的特征方程，它有 n n n个解（重根解算多个），这些解就是矩阵 A A A的特征值，求出特征值再带回到第二个式子中就可以得到对应的特征值 x x x。  
关于这 n n n个解，有三种情况

1.  存在复数解
2.  都是实数解，但存在重根
3.  都是互异实数解

下文都不考虑复数解的情况，先举个求特征值和特征向量的例子：  
求矩阵  A = ( 3 − 1 − 1 3 ) A=\\left(\\begin\{array\}\{rr\}3 & -1 \\\\ -1 & 3\\end\{array\}\\right) A=(3−1−13) 的特征值和特征问量  
特征多项式为：  
 ∣ A − λ E ∣ = ∣ 3 − λ − 1 − 1 3 − λ ∣ = ( 3 − λ ) 2 − 1 = 8 − 6 λ + λ 2 = ( 4 − λ ) ( 2 − λ ) |A-\\lambda E|=\\left|\\begin\{array\}\{cc\}3-\\lambda & -1 \\\\ -1 & 3-\\lambda\\end\{array\}\\right|=(3-\\lambda)^\{2\}-1=8-6 \\lambda+\\lambda^\{2\}=(4-\\lambda)(2-\\lambda) ∣A−λE∣=∣∣∣∣3−λ−1−13−λ∣∣∣∣=(3−λ)2−1=8−6λ\+λ2=(4−λ)(2−λ)所以 A 的特征值为  λ 1 = 2 , λ 2 = 4 \\lambda\_\{1\}=2, \\lambda\_\{2\}=4 λ1=2,λ2=4，当  λ 1 = 2 \\lambda\_\{1\}=2 λ1=2 时, 对应的特征向量应满足  
 ( 3 − 2 − 1 − 1 3 − 2 ) ( x 1 x 2 ) = ( 0 0 ) \\left(\\begin\{array\}\{cc\} 3-2 & -1 \\\\ -1 & 3-2 \\end\{array\}\\right)\\left(\\begin\{array\}\{l\} x\_\{1\} \\\\ x\_\{2\} \\end\{array\}\\right)=\\left(\\begin\{array\}\{l\} 0 \\\\ 0 \\end\{array\}\\right) (3−2−1−13−2)(x1x2)=(00)即 ( 1 − 1 − 1 1 ) ( x 1 x 2 ) = ( 0 0 ) \\left(\\begin\{array\}\{rr\} 1 & -1 \\\\ -1 & 1 \\end\{array\}\\right)\\left(\\begin\{array\}\{l\} x\_\{1\} \\\\ x\_\{2\} \\end\{array\}\\right)=\\left(\\begin\{array\}\{l\} 0 \\\\ 0 \\end\{array\}\\right) (1−1−11)(x1x2)=(00)解得 p 1 = k ( 1 1 ) （ k ≠ 0 ） p\_\{1\}=k\\left(\\begin\{array\}\{l\} 1 \\\\ 1 \\end\{array\}\\right)（k \\neq 0） p1=k(11)（k=0）同理可以求出 λ 2 = 4 \\lambda\_2=4 λ2=4时对应的特征向量，从这个例子我们可以看到，**特征向量是不唯一的**。  
那么特征值具有哪些性质呢？如下：

1.   λ 1 + λ 2 + ⋯ + λ n = a 11 + a 22 + ⋯ + a n n \\lambda\_\{1\}+\\lambda\_\{2\}+\\cdots+\\lambda\_\{n\}=a\_\{11\}+a\_\{22\}+\\cdots+a\_\{n n\} λ1\+λ2\+⋯\+λn=a11\+a22\+⋯\+ann
2.   λ 1 λ 2 ⋯ λ n = ∣ A ∣ \\lambda\_\{1\} \\lambda\_\{2\} \\cdots \\lambda\_\{n\}=|\\boldsymbol\{A\}| λ1λ2⋯λn=∣A∣
3.   φ ( λ ) \\varphi(\\lambda) φ(λ) 是  φ ( A ) \\varphi(A) φ(A) 的特征值，其中  φ ( λ ) = a 0 + a 1 λ + ⋯ + a m λ m \\varphi(\\lambda)=a\_\{0\}+a\_\{1\} \\lambda+\\cdots+a\_\{m\} \\lambda^\{m\} φ(λ)=a0\+a1λ\+⋯\+amλm 是  λ \\lambda λ 的多项式 ,  φ ( A ) = a 0 E + a 1 A + ⋯ + a m A m \\varphi(A)=a\_\{0\}E+a\_\{1\} A+\\cdots +a\_\{m\} A^m φ(A)=a0E\+a1A\+⋯\+amAm是矩阵 A A A的多项式，由此可以得到两个特殊的，(1)  λ k \\lambda^\{k\} λk 是  A k A^\{k\} Ak 的特征值（2） 1 λ \\frac\{1\}\{\\lambda\} λ1 是  A − 1 \\boldsymbol\{A\}^\{-1\} A−1 的特征值
4.  不同特征值对应的特征向量线性无关

## 特征值分解 ##

先引入一个相似矩阵的概念，定义，设 A 、 B A、B A、B都是 n n n阶矩阵，若有可逆矩阵 P P P，使  
 P − 1 A P = B \{P\}^\{-1\} \{A P\}=\{B\} P−1AP=B则称 A A A与 B B B相似，这个过程称为相似变换， P P P称为相似变换矩阵。  
它具有一个很重要的性质：**相似矩阵的特征值相同**

为什么要引入这么一个东西？主要是为了引出相似对角化这个玩意。  
特殊的，如果 A A A与对角矩阵 Λ = ( λ 1 λ 2 ⋱ λ n ) \\boldsymbol\{\\Lambda\}=\\left(\\begin\{array\}\{cccc\}\\lambda\_\{1\} & & & \\\\ & \\lambda\_\{2\} & & \\\\ & & \\ddots & \\\\ & & & \\lambda\_\{n\}\\end\{array\}\\right) Λ=⎝⎜⎜⎛λ1λ2⋱λn⎠⎟⎟⎞相似，即 P − 1 A P = Λ \{P\}^\{-1\} \{A P\}=\{\\Lambda\} P−1AP=Λ 那么 λ 1 , λ 2 , ⋯   , λ n \\lambda\_\{1\}, \\lambda\_\{2\}, \\cdots, \\lambda\_\{n\} λ1,λ2,⋯,λn 是  A \{A\} A 的  n n n 个特征值（相似矩阵和对角矩阵的性质），而  P P P 的列向量  p i p\_i pi 就是  A A A 的对应于特征值 λ i \\lambda\_i λi的特征向量。

把 P P P乘到右边，得到：  
 A = P Λ P − 1 A=P \\Lambda P^\{-1\} A=PΛP−1  
这个式子就是实际中经常用到的**特征值分解**，一个矩阵 A A A可以通过特征值分解得到它的特征值和特征向量（numpy有包可以直接调用） ，但是特征分解只适用于方阵，更普遍的是奇异值分解SVD。

import numpy as np
    from numpy.linalg import eig
    
    a = np.array([[1, 2, 3],[5, 8, 7],[1, 1, 1]])
    e_vals,e_vecs = np.linalg.eig(a)
    
    print(e_vals)
    print(e_vecs)
    # 注意列向量才是特征向量
    [10.254515   -0.76464793  0.51013292]
    [[-0.24970571 -0.89654947  0.54032982]
     [-0.95946634  0.19306928 -0.73818337]
     [-0.13065753  0.39865186  0.40389232]]

从相似对角化的的定义可以看到，我们可以把一个复杂的矩阵 A A A变换成一个很简单的对角矩阵，而这个对角矩阵也同样保留了原来矩阵的特征，且变换的矩阵 P P P就是 A A A的特征向量组成的矩阵，挺神奇！把一个复杂的事物变成具有同样性质的简单事物，进一步我们可以用这个简单的事物代替复杂的事物去做一些操作，从而提高效率或减少复杂度，这在工程上是非常有用的。

但是注意，不是每一个矩阵都能与对角矩阵相似，首先注意到 P P P必须是可逆的，而 P P P又是由特征向量组成，那么换句话说：**当且仅当 A A A有 n n n个线性无关的特征向量时， A A A才能相似对角化**。由这个定理结合特征值的性质4我们可以得到推论：如 果  n n n 阶 矩 阵  A A A 的  n n n 个特征值互不相等（解的情况3） , 则  A A A 可以相似对角化。

那么哪些不可以相似对角化？解的情况2中，重根对应的特征向量个数小于重数的矩阵，比如矩阵 A = ( − 1 1 0 − 4 3 0 1 0 2 ) A=\\left(\\begin\{array\}\{rrr\}-1 & 1 & 0 \\\\ -4 & 3 & 0 \\\\ 1 & 0 & 2\\end\{array\}\\right) A=⎝⎛−1−41130002⎠⎞， λ = 1 \\lambda=1 λ=1是2重根（另外一个根是2），但是对应的线性无关的特征向量只有一个，所以总体上就只有2个线性无关的特征向量（ < 3），故不能相似对角化。

## 对称矩阵的特征值分解 ##

在可相似对角化的矩阵中，对称矩阵（ A T = A A^T=A AT=A）是经常用到，它的性质是：**对称矩阵都有 N 个线性无关的特征向量，且不同特征值对应的特征向量相互正交。**

由此我们可以知道，对称矩阵一定可以相似对角化，而且可以把些特征向量正交单位化而得到一组正交且模为 1 的向量，故实对称矩阵 A 可被分解成：

A = P Λ P − 1 = P A P T A= P\\Lambda P^\{-1\} = P A P^\{\\mathrm\{T\}\} A=PΛP−1=PAPT  
其中， P P P为正交矩阵（ P P T = E PP^T=E PPT=E）

# 奇异值分解SVD #

特征值分解是一个提取矩阵特征很不错的方法，但是它只是对方阵而言的，在现实的世界中，我们看到的大部分矩阵都不是方阵，那么奇异值分解就是一种能适用于任意矩阵分解的方法。

假设矩阵A是一个  m × n m \\times n m×n 的矩阵，那么就可以分解为：  
 A = U Σ V T A=U \\Sigma V^\{T\} A=UΣVT  
U：  m × m m \\times m m×m ，其中的列向量  u ⃗ 1 , u ⃗ 2 , … , u ⃗ m \\vec\{u\}\_\{1\}, \\vec\{u\}\_\{2\}, \\ldots, \\vec\{u\}\_\{m\} u1,u2,…,um 是  A A T A A^\{T\} AAT 的特征向量, 称为矩阵  A A A的左奇异向量。  
V：  n × n n \\times n n×n ,其中的列向量  v ⃗ 1 , v ⃗ 2 , … , v ⃗ m \\vec\{v\}\_\{1\}, \\vec\{v\}\_\{2\}, \\ldots, \\vec\{v\}\_\{m\} v1,v2,…,vm 是  A T A A^\{T\}A ATA 的特征向量, 称为矩阵  A A A的右奇异向量。  
 Σ \\Sigma Σ： m × n m \\times n m×n ，除了主对角线上的元素以外全为0， 主对角线上的元素 σ i \\sigma\_\{i\} σi称为奇异值, σ i = λ i \\sigma\_\{i\}=\\sqrt\{\\lambda\_\{i\}\} σi=λi， λ i \\lambda\_\{i\} λi是 A T A A^\{T\}A ATA的特征值（或 A A T AA^\{T\} AAT，两者特征值相同）。  
另外，U和V都是正交矩阵（因为它们是对称矩阵求出来的呀！）, 即满足  U T U = E , V T V = E U^\{T\} U=E, V^\{T\} V=E UTU=E,VTV=E。  
示意图如下：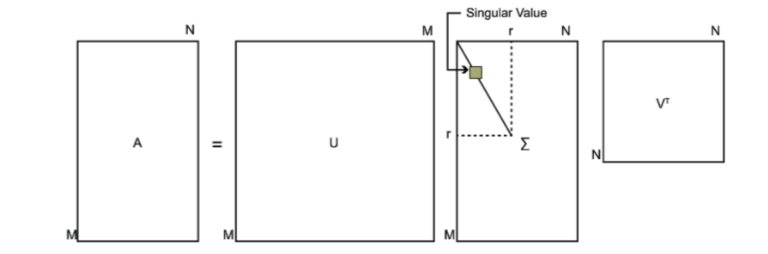  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L01vcmVBY3Rpb25f_size_16_color_FFFFFF_t_70]  
奇异值在矩阵中是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：  
 A m × n = U m × m Σ m × n V n × n T ≈ U m × k Σ k × k V k × n T A\_\{m \\times n\}=U\_\{m \\times m\} \\Sigma\_\{m \\times n\} V\_\{n \\times n\}^\{T\} \\approx U\_\{m \\times k\} \\Sigma\_\{k \\times k\} V\_\{k \\times n\}^\{T\} Am×n=Um×mΣm×nVn×nT≈Um×kΣk×kVk×nT  
其中，k是一个远小于m、n的数。SVD具有的这种特性可以用于PCA降维、数据压缩和去噪等，关于PCA的内容会另写一篇博客。

reference  
<<工程数学线性代数第六版>>  
<<线性代数及其应用>>  
https://www.zhihu.com/question/21874816/answer/181864044  
https://blog.csdn.net/itnerd/article/details/83445155  
https://www.cnblogs.com/pinard/p/6251584.html

如果对你有帮助，请点个赞让我知道:-D

[2020060619500350.jpg_pic_center]: /images/20230209/f62db58df8dc47c8a9d82eea5803a58e.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L01vcmVBY3Rpb25f_size_16_color_FFFFFF_t_70]: /images/20230209/ded7995eedbb4c8084c516b5aeb93e81.png