数据结构零基础，Java语言实现从入门到进阶

清疚 2023-02-19 11:21 53阅读 0赞

数据结构目录

  • 关于数据结构中的基础知识
    • 总结的并不是很到位。
    • 一、数组（Array）
      • 1.1 创建自己的数组以及对数组操作的方法（添加、查询、修改、包含、搜索、删除）
      • 1.2将之前的数组代码修改为泛型
      • 1.3动态数组（自动扩容和自动缩容）
      • 1.4简单的时间复杂度分析
    • 二、栈(Stack)和队列（Queue）
      • 2.1关于栈
      • **2.2程序调用系统栈**
      • 2.3栈的基本实现
      • 2.4关于队列(Queue)
      • 2.5数组队列的基本实现
      • 2.6循环队列的实现
      • 2.7测试数组队列和循环队列二者的性能
    • 小结：动态数组、栈、队列底层依托静态数组，靠的是resize解决固定容量问题！
    • 三、链表LinkedList（真正的动态数据结构、最简单的动态数据结构）
      • 3.1关于链表
      • 3.2链表的基本实现（增加、遍历、查询、修改、删除）
      • 3.3使用链表实现栈(在Stack工程下实现)
      • 3.4比较数组栈和链表栈之间的性能差距
      • 3.5使用链表实现队列（从队首端删除元素，从队尾端插入元素）
      • 3.6移除链表元素（测试自己的链表代码，在题库提交类似的题目时，需将main函数中的内容去掉！！）
        • 3.61不使用虚拟头节点**
        • 3.62使用虚拟头节点
    • 四、递归（Recursion）
      • 4.1使用递归实现求和
      • 4.2运用递归解决链表中删除元素的问题
      • 4.3递归算法的调试（使用打印输出的方式来了解递归调用的过程）
    • 五、二分搜索树（Binary Search Tree）
      • 5.1在了解二分搜索树之前，先了解一下二叉树
      • 5.2二分搜索树的特点
      • 5.3二分搜索树的实现
    • 六、集合和映射（Set and Map）
      • 6.1基于二分搜索树的集合实现
      • 6.2基于链表的集合实现
      • 6.3关于映射
      • 6.4基于链表的映射实现
      • 6.5基于二分搜索树的映射实现
    • 七、优先队列（PriorityQueue）和堆(Heap)
      • 7.1使用二叉树来表示堆，简称二叉堆
      • 7.2利用数组实现最大堆
      • 7.3基于堆的优先队列
    • 八、线段树(Segment Tree)、区间树
      • 8.1关于线段树
      • 8.2实现线段树
    • 九、字典树(Trie),也叫做前缀树
      • 9.1字典树的实现
    • 十、并查集（Union Find）
      • 10.1数组模拟实现并查集
      • 10.2用孩子指向树的结构实现并查集
      • 10.3基于size的优化
      • 10.4基于rank(指树的高度)的优化
      • 10.5路径压缩
    • 十一、AVL树、平衡二叉树
      • 11.1AVL树的实现
      • 11.2基于AVL树的映射实现
      • 11.3基于AVL树的集合实现
    • 十二、红黑树
      • 12.1关于红黑树
      • 12.2 2-3树
      • 12.3 2-3树添加元素的过程
      • 12.4红黑树的实现
      • 12.5红黑树的性能总结
    • 十三、哈希表
      • 实现哈希表（增删改查等方法）

关于数据结构中的基础知识

总结的并不是很到位。

一、数组（Array）

以下代码首先实现了数组的创建，以及对其所创建的数组进行一次二次封装。接着，在Array类中提供了对数组的添加、查询、修改、包含、搜索和删除的方法，以及到后面的使用泛型，动态数组，简单的复杂度分析和均摊复杂度和防止复杂度的震荡。

1.1 创建自己的数组以及对数组操作的方法（添加、查询、修改、包含、搜索、删除）

  1. public class Array { 
  2.     private int[] data;
  3.     private int size;   //data数组中元素的个数
  5.     //构造函数，传入数组的容量为capacity
  6.     public Array(int capacity){ 
  7.         data = new int[capacity];
  8.         size = 0;
  9.     }
  11.     //无参数的构造函数，默认数组的容量capacity=10
  12.     public Array(){ 
  13.         this(10);//通过一个构造方法区调用另一个构造方法，达到代码重用。
  14.     }
  16.     //获取数组中的元素个数
  17.     public int getSize(){ 
  18.         return size;
  19.     }
  21.     //获取数组的容量
  22.     public int getCapacity(){ 
  23.         return data.length;
  24.     }
  26.     //返回数组是否为空
  27.     public boolean isEmpty(){ 
  28.         return size==0;
  29.     }
  31.     //向所有元素后添加一个新元素
  32.     public void addLast(int e){ 
  33.         add(size,e);
  34.     }
  36.     //向所有元素前添加一个新元素
  37.     public void addFirst(int e){ 
  38.         add(0,e);
  39.     }
  42.     //在index位置插入一个新元素e
  43.     public void add(int index,int e) { 
  44.         if (size == data.length){ 
  45.             throw new IllegalArgumentException("Add failed. Array is full");
  46.         }
  48.         if(index <0 || index >size) { 
  49.             throw new IllegalArgumentException("Add failed. Require index >=0 and index <= size");
  50.         }
  52.         for(int i=size-1;i>=index;i--) { 
  53.             data[i + 1] = data[i];
  54.         }
  55.             data[index]=e;
  56.             size++;
  57.     }
  59.     //获取index索引位置的元素
  60.     int get(int index){ 
  61.         if(index<0 || index>=size){ 
  62.             throw new IllegalArgumentException("Get failed. Index is illegal");
  63.         }
  64.         return data[index];
  65.     }
  67.     //修改index索引位置的元素e
  68.     void set(int index,int e){ 
  69.         if(index<0 || index>=size){ 
  70.             throw new IllegalArgumentException("Get failed. index is illegal");
  71.         }
  72.         data[index] = e;
  73.     }
  75.     //查找数组中是否有元素e
  76.     public boolean contains(int e){ 
  77.         for(int i=0;i<size;i++){ 
  78.             if(data[i]==e){ 
  79.                 return true;
  80.             }
  81.         }
  82.         return false;
  83.     }
  85.     //查找数组中元素e所在的索引，如果不存在元素e，则返回-1
  86.     public int find(int e){ 
  87.         for(int i=0;i<size;i++){ 
  88.             if(data[i]==e){ 
  89.                 return i;
  90.             }
  91.         }
  92.         return -1;
  93.     }
  95.     //从数组中删除index位置的元素，返回删除的元素
  96.     public int remove(int index){ 
  97.         if(index<0 || index>=size){ 
  98.             throw new IllegalArgumentException("Remove failed Index is illegal");
  99.         }
  100.         int ret = data[index];
  101.         for(int i=index+1;i<size;i++){ 
  102.             data[i-1] = data[i];
  103.         }
  104.         size--;
  105.         return ret;
  106.     }
  108.     //从数组中删除第一个元素，返回删除的元素
  109.     public int removeFirst(){ 
  110.         return remove(0);
  111.     }
  113.     //从数组中删除最后一个元素，返回删除的元素
  114.     public int removeLast(){ 
  115.         return remove(size-1);
  116.     }
  118.     //从数组中删除元素e
  119.     public void removeElement(int e){ 
  120.         int index = find(e);
  121.         if(index != -1){ 
  122.             remove(index);
  123.         }
  124.     }
  126.     @Override
  127.     public String toString(){ 
  128.         StringBuilder res = new StringBuilder();
  129.         res.append(String.format("Array:size = %d , capacity = %d\n",size,data.length));
  130.         res.append('[');
  131.         for(int i=0;i<size;i++){ 
  132.             res.append(data[i]);
  133.             if(i!=size-1) { 
  134.                 res.append(",");
  135.             }
  136.         }
  137.         res.append(']');
  138.         return res.toString();
  139.     }
  140. }

测试代码如下

  1. public class Main { 
  3.     public static void main(String[] args) { 
  4.       Array arr=new Array(20);
  5.       for(int i=0 ; i<10 ;i++)
  6.           arr.addLast(i);
  7.             System.out.println(arr);
  9.           arr.add(1,100);
  10.             System.out.println(arr);
  12.           arr.addFirst(-1);
  13.             System.out.println(arr);
  15.           arr.remove(2);
  16.             System.out.println(arr);
  18.           arr.removeElement(4);
  19.             System.out.println(arr);
  21.            arr.removeFirst();
  22.             System.out.println(arr);
  23.     }
  24. }

此处为运行结果
在这里插入图片描述

1.2将之前的数组代码修改为泛型

  1. public class Array<E> { 
  2.     private E[] data;
  3.     private int size;   //data数组中元素的个数
  5.     //构造函数，传入数组的容量为capacity
  6.     public Array(int capacity){ 
  7.         data = (E[]) new Object[capacity];
  8.         size = 0;
  9.     }
  11.     //无参数的构造函数，默认数组的容量capacity=10
  12.     public Array(){ 
  13.         this(10);//通过一个构造方法区调用另一个构造方法，达到代码重用。
  14.     }
  16.     //获取数组中的元素个数
  17.     public int getSize(){ 
  18.         return size;
  19.     }
  21.     //获取数组的容量
  22.     public int getCapacity(){ 
  23.         return data.length;
  24.     }
  26.     //返回数组是否为空
  27.     public boolean isEmpty(){ 
  28.         return size==0;
  29.     }
  31.     //向所有元素后添加一个新元素
  32.     public void addLast(E e){ 
  33.         add(size,e);
  34.     }
  36.     //向所有元素前添加一个新元素
  37.     public void addFirst(E e){ 
  38.         add(0,e);
  39.     }
  42.     //在index位置插入一个新元素e
  43.     public void add(int index,E e) { 
  44.         if (size == data.length){ 
  45.             throw new IllegalArgumentException("Add failed. Array is full");
  46.         }
  48.         if(index <0 || index >size) { 
  49.             throw new IllegalArgumentException("Add failed. Require index >=0 and index <= size");
  50.         }
  52.         for(int i=size-1;i>=index;i--) { 
  53.             data[i + 1] = data[i];
  54.         }
  55.             data[index]=e;
  56.             size++;
  57.     }
  59.     //获取index索引位置的元素
  60.     public E get(int index){ 
  61.         if(index<0 || index>=size){ 
  62.             throw new IllegalArgumentException("Get failed. Index is illegal");
  63.         }
  64.         return data[index];
  65.     }
  67.     //修改index索引位置的元素e
  68.     public void set(int index,E e){ 
  69.         if(index<0 || index>=size){ 
  70.             throw new IllegalArgumentException("Get failed. index is illegal");
  71.         }
  72.         data[index] = e;
  73.     }
  75.     //查找数组中是否有元素e
  76.     public boolean contains(E e){ 
  77.         for(int i=0;i<size;i++){ 
  78.             if(data[i].equals(e)){ 
  79.                 return true;
  80.             }
  81.         }
  82.         return false;
  83.     }
  85.     //查找数组中元素e所在的索引，如果不存在元素e，则返回-1
  86.     public int find(E e){ 
  87.         for(int i=0;i<size;i++){ 
  88.             if(data[i].equals(e)){ 
  89.                 return i;
  90.             }
  91.         }
  92.         return -1;
  93.     }
  95.     //从数组中删除index位置的元素，返回删除的元素
  96.     public E remove(int index){ 
  97.         if(index<0 || index>=size){ 
  98.             throw new IllegalArgumentException("Remove failed Index is illegal");
  99.         }
  100.         E ret = data[index];
  101.         for(int i=index+1;i<size;i++){ 
  102.             data[i-1] = data[i];
  103.         }
  104.         size--;
  105.         data[size]=null;
  106.         return ret;
  107.     }
  109.     //从数组中删除第一个元素，返回删除的元素
  110.     public E removeFirst(){ 
  111.         return remove(0);
  112.     }
  114.     //从数组中删除最后一个元素，返回删除的元素
  115.     public E removeLast(){ 
  116.         return remove(size-1);
  117.     }
  119.     //从数组中删除元素e
  120.     public void removeElement(E e){ 
  121.         int index = find(e);
  122.         if(index != -1){ 
  123.             remove(index);
  124.         }
  125.     }
  127.     @Override
  128.     public String toString(){ 
  129.         StringBuilder res = new StringBuilder();
  130.         res.append(String.format("Array:size = %d , capacity = %d\n",size,data.length));
  131.         res.append('[');
  132.         for(int i=0;i<size;i++){ 
  133.             res.append(data[i]);
  134.             if(i!=size-1) { 
  135.                 res.append(",");
  136.             }
  137.         }
  138.         res.append(']');
  139.         return res.toString();
  140.     }
  141. }

测试

  1. public class Main { 
  3.     public static void main(String[] args) { 
  4.       Array<Integer> arr=new Array<Integer>(20);//数组中存放的都是Integer类型
  5.       for(int i=0 ; i<10 ;i++)
  6.           arr.addLast(i);
  7.             System.out.println(arr);
  9.           arr.add(1,100);
  10.             System.out.println(arr);
  12.           arr.addFirst(-1);
  13.             System.out.println(arr);
  15.           arr.remove(2);
  16.             System.out.println(arr);
  18.           arr.removeElement(4);
  19.             System.out.println(arr);
  21.            arr.removeFirst();
  22.             System.out.println(arr);
  23.     }
  24. }

创建一个学生数组，泛型

  1. public class Student { 
  2.     private String name;
  3.     private int score;
  5.     public Student(String studentName,int studentScore){ 
  6.         name=studentName;
  7.         score=studentScore;
  8.     }
  10.     @Override
  11.     public String toString(){ 
  12.         return String.format("Student(name: %s, score: %d)",name,score);
  13.     }
  15.     public static void main(String[] args){ 
  16.         Array<Student> arr = new Array<Student>();
  17.         arr.addLast(new Student("Alice",100));
  18.         arr.addLast(new Student("Bob",70));
  19.         arr.addLast(new Student("Tracy",80));
  20.         System.out.println(arr);
  21.     }
  22. }

输出结果
在这里插入图片描述

1.3动态数组（自动扩容和自动缩容）

增加了扩容方法和缩容逻辑

  1. public class Array<E> { 
  2.     private E[] data;
  3.     private int size;   //data数组中元素的个数
  5.     //构造函数，传入数组的容量为capacity
  6.     public Array(int capacity){ 
  7.         data = (E[]) new Object[capacity];
  8.         size = 0;
  9.     }
  11.     //无参数的构造函数，默认数组的容量capacity=10
  12.     public Array(){ 
  13.         this(10);//通过一个构造方法区调用另一个构造方法，达到代码重用。
  14.     }
  16.      public Array(E[] arr){ 
  17.         data =(E[]) new Object[arr.length];
  18.         for(int i=0;i<arr.length;i++){ 
  19.             data[i] = arr[i];
  20.         }
  21.         size = arr.length;
  22.     }
  24.     //获取数组中的元素个数
  25.     public int getSize(){ 
  26.         return size;
  27.     }
  29.     //获取数组的容量
  30.     public int getCapacity(){ 
  31.         return data.length;
  32.     }
  34.     //返回数组是否为空
  35.     public boolean isEmpty(){ 
  36.         return size==0;
  37.     }
  39.     //向所有元素后添加一个新元素
  40.     public void addLast(E e){ 
  41.         add(size,e);
  42.     }
  44.     //向所有元素前添加一个新元素
  45.     public void addFirst(E e){ 
  46.         add(0,e);
  47.     }
  50.     //在第index位置插入一个新元素e
  51.     public void add(int index,E e) { 
  53.         if(index <0 || index >size) { 
  54.             throw new IllegalArgumentException("Add failed. Require index >=0 and index <= size");
  55.         }
  57.         if (size == data.length){ 
  58.             resize(2 * data.length);
  59.         }
  61.         for(int i=size-1;i>=index;i--) { 
  62.             data[i + 1] = data[i];
  63.         }
  64.             data[index]=e;
  65.             size++;
  66.     }
  68.     //获取index索引位置的元素
  69.     public E get(int index){ 
  70.         if(index<0 || index>=size){ 
  71.             throw new IllegalArgumentException("Get failed. Index is illegal");
  72.         }
  73.         return data[index];
  74.     }
  76.     //修改index索引位置的元素e
  77.     public void set(int index,E e){ 
  78.         if(index<0 || index>=size){ 
  79.             throw new IllegalArgumentException("Get failed. index is illegal");
  80.         }
  81.         data[index] = e;
  82.     }
  84.     //查找数组中是否有元素e
  85.     public boolean contains(E e){ 
  86.         for(int i=0;i<size;i++){ 
  87.             if(data[i].equals(e)){ 
  88.                 return true;
  89.             }
  90.         }
  91.         return false;
  92.     }
  94.     //查找数组中元素e所在的索引，如果不存在元素e，则返回-1
  95.     public int find(E e){ 
  96.         for(int i=0;i<size;i++){ 
  97.             if(data[i].equals(e)){ 
  98.                 return i;
  99.             }
  100.         }
  101.         return -1;
  102.     }
  104.     //从数组中删除index位置的元素，返回删除的元素
  105.     public E remove(int index){ 
  106.         if(index<0 || index>=size){ 
  107.             throw new IllegalArgumentException("Remove failed Index is illegal");
  108.         }
  109.         E ret = data[index];
  110.         for(int i=index+1;i<size;i++){ 
  111.             data[i-1] = data[i];
  112.         }
  113.         size--;
  114.         data[size]=null;
  116.         //对数组缩容
  117.         if(size==data.length / 2){ 
  118.             resize(data.length / 2);
  119.         }
  121.         return ret;
  122.     }
  124.     //从数组中删除第一个元素，返回删除的元素
  125.     public E removeFirst(){ 
  126.         return remove(0);
  127.     }
  129.     //从数组中删除最后一个元素，返回删除的元素
  130.     public E removeLast(){ 
  131.         return remove(size-1);
  132.     }
  134.     //从数组中删除元素e
  135.     public void removeElement(E e){ 
  136.         int index = find(e);
  137.         if(index != -1){ 
  138.             remove(index);
  139.         }
  140.     }
  142.     public void swap(int i,int j){ 
  143.         if(i<0 || i>=size || j<0 || j>=size){ 
  144.             throw new IllegalArgumentException("index is illegal");
  145.         }
  146.         E t = data[i];
  147.         data[i] = data[j];
  148.         data[j] = t;
  149.     }
  151.     @Override
  152.     public String toString(){ 
  153.         StringBuilder res = new StringBuilder();
  154.         res.append(String.format("Array:size = %d , capacity = %d\n",size,data.length));
  155.         res.append('[');
  156.         for(int i=0;i<size;i++){ 
  157.             res.append(data[i]);
  158.             if(i!=size-1) { 
  159.                 res.append(",");
  160.             }
  161.         }
  162.         res.append(']');
  163.         return res.toString();
  164.     }
  166.     //数组扩容
  167.     private void resize(int newCapacity){ 
  168.         E[] newData =(E[]) new Object[newCapacity];
  169.         for(int i=0;i<size;i++){ 
  170.             newData[i]=data[i];
  171.         }
  172.             data=newData;
  173.     }
  174. }

测试

  1. public class Main { 
  3.     public static void main(String[] args) { 
  4.       Array<Integer> arr=new Array<>();//数组中存放的都是Integer类型
  5.       for(int i=0 ; i<10 ;i++)
  6.           arr.addLast(i);
  7.           System.out.println(arr);
  9.           arr.add(1, 100);
  10.           System.out.println(arr);
  12.           arr.addFirst(-1);
  13.           System.out.println(arr);
  15.           arr.remove(2);
  16.             System.out.println(arr);
  18.           arr.removeElement(4);
  19.             System.out.println(arr);
  21.             arr.removeFirst();
  22.             System.out.println(arr);
  23.     }
  24. }

运行结果：当数组个数为原有容量的二分之一时，原数组容量也随之缩小二分之一；当数组个数超出原数组容量时，数组容量将会扩容为原来容量的二倍。
在这里插入图片描述

1.4简单的时间复杂度分析

在这里插入图片描述
为什么要用大O，叫做O(n)？
忽略常数。实际时间T=c1*n+c2

线性时间的算法：
T=2n+2 — O(n)
T=2000n+10000 — O(n)
O的表示实际上叫做渐进复杂度。渐进(描述n趋近于无穷的情况)

T=1nn+0 — O(n^2)
n越大，O(n)级别的算法远远快于O(n^2)级别的算法
T=2nn+300n+10 — O(n^2) 300n这个低阶项会被忽略掉

分析动态数组的时间复杂度
添加操作：最坏情况，三者均为O(n)操作，因为有resize 为O(n)操作
addLast(e) O(1)操作
addFirst(e) O(n)操作
add(index,e) O(n/2)=O(n) 操作

删除操作：最坏情况，三者均为O(n)操作，因为有resize 为O(n)操作
removeLast(e) O(1)
removeFirst(e) O(n)
remove(index,e) O(n/2)=O(n)

修改操作：
set(index,e) O(1)操作

查找操作：
get(index) O(1)操作
contains(e) O(n)操作
find(e) O(n)操作

在这里插入图片描述
resize复杂度分析
在这里插入图片描述
resize O(n) 操作
9次addLast操作，触发resize，总共进行了17次基本操作，平均，每次addLast操作，进行2次基本操作。
假设capacity = n，n+1次addLast，触发resize，总共进行2n+1次基本操作，平均，每次addLast操作，进行2次基本操作。这样均摊计算，时间复杂度是O(1)的！这种思想为均摊复杂度（amortized time complexity）其思想是一个相对比较耗时的操作，如果我们能够保证它不会每次都触发，这个耗时的操作相应的时间可以分摊到其他操作上。

addLast的均摊复杂度为O(1),同理，removeLast操作，均摊复杂度也为O(1).

当同时看addLast和removeLast操作的时候，出现了复杂度震荡（在调用addLast方法时，出现了capacity的扩容；当调用removeLast方法时，又出现了capacity的缩容，其都是O(n)操作）

出现复杂度震荡的原因：removeLast时resize过于着急
解决方案：当size==capacity/4时，才将capacity缩容减半

解决方案运用到代码中：修改缩容部分的代码，修改后如下：
在这里插入图片描述

二、栈(Stack)和队列（Queue）

2.1关于栈

1.栈也是一种线性结构
2.相比数组，栈对应的操作时数组的子集
3.只能从一端添加元素，也只能从一端取出元素
4.这一端称为栈顶
5.栈是一种先进后出的数据结构

以下图示展示压栈，弹栈，以及先进后出
在这里插入图片描述
在这里插入图片描述弹栈也可以叫做出栈

2.2程序调用系统栈

在这里插入图片描述

2.3栈的基本实现

首先创建一个接口

  1. public interface Stack<E> { 
  3.     int getSize();
  4.     boolean isEmpty();
  5.     void push(E e);//入栈
  6.     E pop();//出栈
  7.     E peek();//栈顶
  8. }

接着将之前的动态数组粘贴到当前的包中，并增加以下两个新的方法
在这里插入图片描述
接着创建一个ArrayStack类

  1. public class ArrayStack<E> implements Stack<E> { 
  3.     Array<E> array;
  5.     public ArrayStack(int capacity){ 
  6.         array = new Array<>(capacity);
  7.     }
  9.     public ArrayStack(){ 
  10.         array = new Array<>();
  11.     }
  13.     @Override
  14.     public int getSize(){ 
  15.         return array.getSize();
  16.     }
  18.     @Override
  19.     public boolean isEmpty(){ 
  20.         return array.isEmpty();
  21.     }
  23.     public int getCapacity(){ 
  24.         return array.getCapacity();
  25.     }
  27.     @Override
  28.     public void push(E e){   //压栈
  29.         array.addLast(e);
  30.     }
  32.     @Override
  33.     public E pop(){      //弹栈
  34.         return array.removeLast();
  35.     }
  37.     @Override
  38.     public E peek(){ 
  39.         return array.getLast();
  40.     }
  42.     @Override
  43.     public String toString(){ 
  44.         StringBuilder res = new StringBuilder();
  45.         res.append("Stack: ");
  46.         res.append('[');
  47.         for(int i=0;i<array.getSize();i++){ 
  48.             res.append(array.get(i));
  49.             if(i != array.getSize()-1){ 
  50.                 res.append(", ");
  51.             }
  52.         }
  53.                 res.append("] top");//显示栈顶元素
  54.             return res.toString();
  55.     }
  56. }

测试类

  1. public class Main { 
  3.     public static void main(String[] args) { 
  5.         ArrayStack<Integer> stack = new ArrayStack<>();
  7.         for(int i=0;i<5;i++){ 
  8.             stack.push(i);  //入栈操作
  9.             System.out.println(stack);
  10.         }
  12.         stack.pop();    //出栈操作
  13.         System.out.println(stack);
  14.     }
  15. }

运行结果

最右边的是栈顶元素在这里插入图片描述

2.4关于队列(Queue)

1.队列也是一种线性结构
2.相比数组，队列对应的操作是数组的子集
3.只能从一端（队尾）添加元素，只能从另一端（队首）取出元素
4.队列是一种先进先出的数据结构

以下图示展现队列以及先进先出：

在这里插入图片描述

2.5数组队列的基本实现

首先创建一个Queue接口

  1. public interface Queue<E> { 
  3.     int getSize();
  4.     boolean isEmpty();
  5.     void enqueue(E e); //入队
  6.     E dequeue();    //出队
  7.     E getFront();   //队首
  8. }

接着将上面栈中的Array类复制到Queue包中
然后再创建一个ArrayQueue类并进行测试

  1. public class ArrayQueue<E> implements Queue<E> { 
  3.     private Array<E> array;
  5.     public ArrayQueue(int capacity){ 
  6.         array = new Array<>(capacity);
  7.     }
  9.     public ArrayQueue(){ 
  10.         array = new Array<>();
  11.     }
  13.     @Override
  14.     public int getSize(){ 
  15.         return array.getSize();
  16.     }
  18.     @Override
  19.     public boolean isEmpty(){ 
  20.         return array.isEmpty();
  21.     }
  23.     public int getCapacity(){ 
  24.         return array.getCapacity();
  25.     }
  27.     @Override
  28.     public void enqueue(E e){ 
  29.         array.addLast(e);
  30.     }
  32.     @Override
  33.     public E dequeue(){ 
  34.         return array.removeFirst();
  35.     }
  37.     @Override
  38.     public E getFront(){ 
  39.         return array.getFirst();
  40.     }
  42.     @Override
  43.     public String toString(){ 
  44.         StringBuilder res = new StringBuilder();
  45.         res.append("Queue: ");
  46.         res.append("front ["); //显示队首
  47.         for(int i=0;i<array.getSize();i++){ 
  48.             res.append(array.get(i));
  49.             if(i != array.getSize()-1){ 
  50.                 res.append(", ");
  51.             }
  52.         }
  53.             res.append("] tail");//显示队尾
  54.             return res.toString();
  55.     }
  57.     public static void main(String[] args){ 
  58.         ArrayQueue<Integer> queue = new ArrayQueue<>();
  59.         for(int i=0;i<10;i++){ 
  60.             queue.enqueue(i);
  61.             System.out.println(queue);
  63.             if(i % 3 == 2){ 
  64.                 queue.dequeue();
  65.                 System.out.println(queue);
  66.             }
  67.         }
  68.     }
  69. }

运行结果如下（每添加3个元素后从队首往出拿一个）
在这里插入图片描述

2.6循环队列的实现

  1. public class LoopQueue<E> implements Queue<E> { 
  3.     private E[] data;
  4.     private int front,tail; //队首，队尾
  5.     private int size;
  7.     public LoopQueue(int capacity){ 
  8.         data =(E[]) new Object[capacity + 1];
  9.         front = 0;
  10.         tail = 0;
  11.         size = 0;
  12.     }
  14.     public LoopQueue(){ 
  15.         this(10);
  16.     }
  18.     public int getCapacity(){ 
  19.         return data.length-1;
  20.     }
  22.     @Override
  23.     public boolean isEmpty(){ 
  24.         return front == tail;
  25.     }
  27.     @Override
  28.     public int getSize(){ 
  29.         return size;
  30.     }
  32.     //循环队列的入队过程
  33.     @Override
  34.     public void enqueue(E e){ 
  35.         if((tail+1) % data.length == front){ 
  36.             resize(getCapacity() * 2);
  37.         }
  38.         data[tail]=e;
  39.         tail = (tail+1)% data.length;
  40.         size++;
  41.     }
  43.     //循环队列出队过程
  44.     @Override
  45.     public E dequeue(){ 
  46.         if(isEmpty()){ 
  47.             throw new IllegalArgumentException("Cannot dequeue from an empty queue");
  48.         }
  49.         E ret = data[front];
  50.         data[front]=null;
  51.         front = (front + 1) % data.length;
  52.         size--;
  54.         //缩容操作
  55.         if(size==getCapacity()/4 && getCapacity()/2 !=0){ 
  56.             resize(getCapacity()/2);
  57.         }
  58.         return ret;
  59.     }
  61.     @Override
  62.     public E getFront(){ 
  63.         if(isEmpty()){ 
  64.             throw new IllegalArgumentException("Queue is empty");
  65.         }
  66.         return data[front];
  67.     }
  70.     //数组扩容
  71.     private void resize(int newCapacity){ 
  72.         E[] newData =(E[]) new Object[newCapacity + 1];
  73.         for(int i=0;i<size;i++){ 
  74.             newData[i] = data[(i+front) % data.length];
  75.         }
  77.         data=newData;
  78.         front=0;
  79.         tail=size;
  80.     }
  82.     @Override
  83.     public String toString(){ 
  84.         StringBuilder res = new StringBuilder();
  85.         res.append(String.format("Queue: size = %d , capacity = %d\n", size, getCapacity()));
  86.         res.append("front [");
  87.         for(int i = front; i!=tail;i=(i+1)%data.length){ 
  88.             res.append(data[i]);
  89.             if((i+1)%data.length != tail){ 
  90.                 res.append(", ");
  91.             }
  92.         }
  93.         res.append("] tail");
  94.         return res.toString();
  95.     }
  97.     public static void main(String[] args){ 
  98.         LoopQueue<Integer> queue = new LoopQueue<>();
  99.         for(int i=0;i<10;i++){ 
  100.             queue.enqueue(i);
  101.             System.out.println(queue);
  103.         if(i%3 == 2){ 
  104.             queue.dequeue();
  105.             System.out.println(queue);
  106.             }
  107.         }
  108.     }
  109. }

运行结果：
每次入队3个元素后都会进行一次出队操作，相应的，若数组中的元素比原容量的二分之一还要小，则进行一次缩容操作；若数组中的元素个数大于容量个数，则进行一次扩容操作！
在这里插入图片描述

2.7测试数组队列和循环队列二者的性能

  1. import java.util.Random;
  2. public class Main { 
  3.     //测试使用q运行opCount个enqueue和dequeue操作所需要的时间，单位秒
  4.     private static double testQueue(Queue<Integer> q,int opCount){ 
  5.         long startTime = System.nanoTime();
  6.         Random random = new Random();
  8.         for(int i=0;i<opCount;i++){ 
  9.             q.enqueue(random.nextInt(Integer.MAX_VALUE));
  10.         }
  12.         for(int i=0;i<opCount;i++){ 
  13.             q.dequeue();
  14.         }
  16.         long endTime = System.nanoTime();
  17.         return (endTime-startTime)/1000000000.0;
  18.     }
  20.     public static void main(String[] args){ 
  21.         int opCount = 100000;
  22.         ArrayQueue<Integer> arrayQueue = new ArrayQueue<>();
  23.         double time1 = testQueue(arrayQueue,opCount);
  24.         System.out.println("ArrayQueue,time: "+time1+"s");
  26.         LoopQueue<Integer> loopQueue = new LoopQueue<>();
  27.         double time2 = testQueue(loopQueue,opCount);
  28.         System.out.println("LoopQueue,time: "+time2+"s");
  29.     }
  30. }

运行结果如下：
注：不同的计算机性能不同，所测试出的结果也不相同，但肯定的是，循环队列的性能要比数组队列的要好很多！
在这里插入图片描述

小结：动态数组、栈、队列底层依托静态数组，靠的是resize解决固定容量问题！

三、链表LinkedList（真正的动态数据结构、最简单的动态数据结构）

3.1关于链表

1.数据存储在”节点（Node）“中
2.优点：真正的动态，不需要处理固定容量的问题
3.缺点：丧失了随机访问能力

在这里插入图片描述

3.2链表的基本实现（增加、遍历、查询、修改、删除）

  1. public class LinkedList<E> { 
  2.     private class Node{ 
  3.         public E e;
  4.         public Node next;
  6.         public Node(E e,Node next){ 
  7.             this.e=e;
  8.             this.next=next;
  9.         }
  11.         public Node(E e){ 
  12.             this(e,null);
  13.         }
  15.         public Node(){ 
  16.             this(null,null);
  17.         }
  19.         @Override
  20.         public String toString(){ 
  21.             return e.toString();
  22.         }
  23.     }
  25.     private Node dummyHead;//虚拟头节点
  26.     private int size;//个数
  28.     public LinkedList(){ 
  29.         dummyHead=new Node(null,null);
  30.         size=0;
  31.     }
  33.     //获取链表中的元素个数
  34.     public int getSize(){ 
  35.         return size;
  36.     }
  38.     //返回链表是否为空
  39.     public boolean isEmpty(){ 
  40.         return size==0;
  41.     }
  43.     //在链表的index（从0开始）位置添加新的元素e
  44.     //在链表中不是一个常用的操作，练习用
  45.     public void add(int index, E e){ 
  46.         if(index<0 || index>size){ 
  47.             throw new IllegalArgumentException("Add failed Illegal index");
  48.         }
  50.             Node prev = dummyHead;
  51.             for(int i=0;i<index;i++){ 
  52.                 prev=prev.next;
  53.             }
  55. // Node node = new Node(e);
  56. // node.next = prev.next;
  57. // prev.next = node;
  59.             //以上三行代码可以用以下一行代码表示
  60.             prev.next = new Node(e,prev.next);
  61.             size++;
  62.     }
  64.     //在链表头添加新的元素e
  65.     public void addFirst(E e){ 
  66.         add(0,e);
  67.     }
  69.     //在链表末尾添加新的元素e
  70.     public void addLast(E e){ 
  71.         add(size,e);
  72.     }
  74.     //获得链表的第index（从0开始）个位置的元素
  75.     //在链表中不是一个常用操作，练习用
  76.     public E get(int index){ 
  77.         if(index < 0 || index >=size){ 
  78.             throw new IllegalArgumentException("Get failed Illegal index");
  79.         }
  81.         Node cur = dummyHead.next;
  82.         for(int i = 0;i<index;i++){ 
  83.             cur = cur.next;
  84.         }
  85.         return cur.e;
  86.     }
  88.     //获得链表的第一个元素
  89.     public E getFirst(){ 
  90.         return get(0);
  91.     }
  93.     //获得链表的最后一个元素
  94.     public E getLast(){ 
  95.         return get(size-1);
  96.     }
  98.     //修改链表的第index（从0开始）个位置的元素e
  99.     //在链表中不是一个常用操作，练习用
  100.     public void set(int index,E e){ 
  101.         if(index<0 || index>= size){ 
  102.             throw new IllegalArgumentException("Set failed Illegal index");
  103.         }
  105.         Node cur = dummyHead.next;
  106.         for(int i=0;i<index;i++){ 
  107.             cur=cur.next;
  108.         }
  109.             cur.e=e;
  110.     }
  112.     //查找链表中是否含有元素e
  113.     public boolean contains(E e){ 
  114.         Node cur = dummyHead.next;
  115.         while(cur!=null){ 
  116.             if(cur.e.equals(e)){ 
  117.                 return true;
  118.             }
  119.             cur=cur.next;
  120.         }
  121.             return false;
  122.     }
  124.     //从链表中删除index（从0开始）位置的元素，返回删除的元素
  125.     //在链表中不是一个常用的操作，练习用
  126.     public E remove(int index){ 
  127.         if(index<0 || index>=size){ 
  128.             throw new IllegalArgumentException("Remove failed Index is illegal");
  129.         }
  130.         Node prev = dummyHead;
  131.         for(int i=0;i<index;i++){ 
  132.             prev = prev.next;
  133.         }
  135.         Node retNode=prev.next;
  136.         prev.next = retNode.next;
  137.         retNode.next=null;
  138.         size--;
  139.         return retNode.e;
  140.     }
  142.     //从链表中删除最后一个元素，返回删除元素
  143.     public E removeFirst(){ 
  144.         return remove(0);
  145.     }
  147.     //从链表中删除最后一个元素，返回删除元素
  148.     public E removeLast(){ 
  149.         return remove(size-1);
  150.     }
  152.      //从链表中删除元素e
  153.     public void removeElement(E e){ 
  154.         Node prev = dummyHead;
  155.         while(prev.next != null){ 
  156.             if(prev.next.e.equals(e)){ 
  157.                 break;
  158.             }
  159.             prev=prev.next;
  160.         }
  161.         if(prev.next != null){ 
  162.             Node delNode = prev.next;
  163.             prev.next = delNode.next;
  164.             delNode.next = null;
  165.         }
  166.     }
  168.     @Override
  169.     public String toString(){ 
  170.         StringBuilder res = new StringBuilder();
  171.         Node cur = dummyHead.next;
  172.         while(cur!=null){ 
  173.             res.append(cur+"->");
  174.             cur=cur.next;
  175.         }
  176.         res.append("NULL");
  177.         return res.toString();
  178.     }
  179. }

测试

  1. public class Main { 
  2.     public static void main(String[] args){ 
  3.         LinkedList<Integer> linkedList = new LinkedList<>();
  4.         for(int i=0;i<5;i++){ 
  5.             //从头添加元素
  6.             linkedList.addFirst(i);
  7.             System.out.println(linkedList);
  8.         }
  10.         //从索引为2的地方添加一个666元素
  11.         linkedList.add(2,666);
  12.         System.out.println(linkedList);
  14.         System.out.println("==========");
  16.         //删除元素
  17.         linkedList.remove(2);
  18.         System.out.println(linkedList);
  20.         linkedList.removeFirst();
  21.         System.out.println(linkedList);
  23.         linkedList.removeLast();
  24.         System.out.println(linkedList);
  26.     }
  27. }

运行结果如下
在这里插入图片描述

3.3使用链表实现栈(在Stack工程下实现)

  1. public class LinkedListStack<E> implements Stack<E>{ 
  2.     private LinkedList<E> list;
  4.     public LinkedListStack(){ 
  5.         list = new LinkedList<>();
  6.     }
  8.     @Override
  9.     public int getSize(){ 
  10.         return list.getSize();
  11.     }
  13.     @Override
  14.     public boolean isEmpty(){ 
  15.         return list.isEmpty();
  16.     }
  18.     @Override
  19.     public void push(E e){ 
  20.         list.addFirst(e);
  21.     }
  23.     @Override
  24.     public E pop(){ 
  25.         return list.removeFirst();
  26.     }
  28.     @Override
  29.     public E peek(){ 
  30.         return list.getFirst();
  31.     }
  33.     @Override
  34.     public String toString(){ 
  35.         StringBuilder res=new StringBuilder();
  36.         res.append("Stack: top ");
  37.         res.append(list);
  38.         return res.toString();
  39.     }
  41.     public static void main(String[] args) { 
  43.         LinkedListStack<Integer> stack = new LinkedListStack<>();
  45.         for(int i=0;i<5;i++){ 
  46.             stack.push(i);  //入栈操作
  47.             System.out.println(stack);
  48.         }
  50.         stack.pop();    //出栈操作
  51.         System.out.println(stack);
  52.     }
  53. }

运行结果
在这里插入图片描述

3.4比较数组栈和链表栈之间的性能差距

  1. import java.util.Random;
  2. public class Main { 
  4.     //测试使用stack运行opCount个push和pop操作所需要的时间，单位秒
  5.     private static double testStack(Stack<Integer> stack,int opCount){ 
  6.         long startTime = System.nanoTime();
  8.         Random random = new Random();
  9.         for(int i=0;i<opCount;i++){ 
  10.             stack.push(random.nextInt(Integer.MAX_VALUE));
  11.         }
  13.         for(int i=0;i<opCount;i++){ 
  14.             stack.pop();
  15.         }
  17.         long endTime=System.nanoTime();
  18.         return (endTime-startTime)/1000000000.0;
  19.     }
  21.     public static void main(String[] args){ 
  22.         int opCpunt=100000;
  24.         ArrayStack<Integer> arrayStack=new ArrayStack<>();
  25.         double time1=testStack(arrayStack,opCpunt);
  26.         System.out.println("ArrayStack,time: "+time1+"s");
  28.         LinkedListStack<Integer> linkedListStack = new LinkedListStack<>();
  29.         double time2 = testStack(linkedListStack,opCpunt);
  30.         System.out.println("LinkedListStack,time: "+time2+"s");
  31.     }
  32. }

运行结果：
实际上，无论是链表栈还是数组栈，他们的各项操作中都属于同一时间复杂度的，所以在不同情况下谁比谁耗时长一些或短一些都是很正常的，而且与JVM的版本号和电脑的操作系统有一定的关系。二者在复杂度上面没有巨大的差异。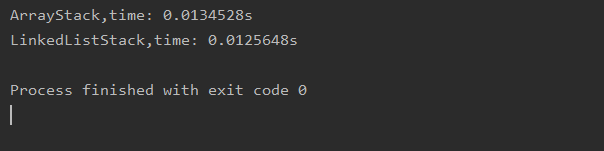
在这里插入图片描述

3.5使用链表实现队列（从队首端删除元素，从队尾端插入元素）

  1. public class LinkedListQueue<E> implements Queue<E> { 
  2.     private class Node{ 
  3.         public E e;
  4.         public Node next;
  6.         public Node(E e,Node next){ 
  7.             this.e=e;
  8.             this.next=next;
  9.         }
  11.         public Node(E e){ 
  12.             this(e,null);
  13.         }
  15.         public Node(){ 
  16.             this(null,null);
  17.         }
  19.         @Override
  20.         public String toString(){ 
  21.             return e.toString();
  22.         }
  23.     }
  25.     private Node head,tail;
  26.     private int size;
  28.     public LinkedListQueue(){ 
  29.         head = null;
  30.         tail = null;
  31.         size = 0;
  32.     }
  34.     @Override
  35.     public int getSize(){ 
  36.         return size;
  37.     }
  39.     @Override
  40.     public boolean isEmpty(){ 
  41.         return size==0;
  42.     }
  44.     //入队操作
  45.     @Override
  46.     public void enqueue(E e){ 
  47.         if(tail==null){ 
  48.             tail=new Node(e);
  49.             head=tail;
  50.         }else{ 
  51.             tail.next=new Node(e);
  52.             tail=tail.next;
  53.         }
  54.         size++;
  55.     }
  57.     //出队操作
  58.     @Override
  59.     public E dequeue(){ 
  60.         if(isEmpty()){ 
  61.             throw new IllegalArgumentException("Cannot dequeue from an empty queue");
  62.         }
  63.         Node retNode=head;
  64.         head=head.next;
  65.         retNode.next=null;
  67.         if(head==null){ 
  68.             tail=null;
  69.         }
  70.         size--;
  71.         return retNode.e;
  72.     }
  74.     //查看队首
  75.     @Override
  76.     public E getFront(){ 
  77.         if(isEmpty()){ 
  78.             throw new IllegalArgumentException("Queue is Empty");
  79.         }
  80.         return head.e;
  81.     }
  83.     @Override
  84.     public String toString(){ 
  85.         StringBuilder res = new StringBuilder();
  86.         res.append("Queue: front ");
  88.         Node cur = head;
  89.         while(cur!=null){ 
  90.             res.append(cur+"->");
  91.             cur=cur.next;
  92.         }
  93.         res.append("NULL tail");
  94.         return res.toString();
  95.     }
  97.     public static void main(String[] args){ 
  98.         LinkedListQueue<Integer> queue = new LinkedListQueue<>();
  99.         for(int i=0;i<10;i++){ 
  100.             queue.enqueue(i);
  101.             System.out.println(queue);
  103.             //每次入队3个元素就出队一个元素
  104.             if(i%3==2){ 
  105.                 queue.dequeue();
  106.                 System.out.println(queue);
  107.             }
  108.         }
  109.     }
  110. }

运行结果：
每次入队三个元素将会出队一个
在这里插入图片描述

3.6移除链表元素（测试自己的链表代码，在题库提交类似的题目时，需将main函数中的内容去掉！！）

删除链表中等于给定值 val 的所有节点。
示例:
输入: 1->2->6->3->4->5->6, val = 6
输出: 1->2->3->4->5

3.61不使用虚拟头节点**

首先创建一个ListNode类

  1. public class ListNode { 
  2.     public int val;
  3.     public ListNode next;
  5.     public ListNode(int x){ 
  6.         val = x;
  7.     }
  9.     //链表节点的构造函数
  10.     //使用arr为参数，创建一个链表，当前的ListNode为链表头节点
  11.     public ListNode(int[] arr){ 
  12.         if(arr == null || arr.length == 0){ 
  13.             throw new IllegalArgumentException("arr cannot be empty");
  14.         }
  15.         this.val=arr[0];
  16.         ListNode cur = this;
  17.         for(int i=1;i<arr.length;i++){ 
  18.             cur.next = new ListNode(arr[i]);
  19.             cur = cur.next;
  20.         }
  21.     }
  23.     //以当前节点为头节点的链表信息字符串
  24.     @Override
  25.     public String toString(){ 
  26.         StringBuilder res = new StringBuilder();
  27.         ListNode cur = this;
  28.         while(cur != null){ 
  29.             res.append(cur.val + "->");
  30.             cur = cur.next;
  31.         }
  32.             res.append("NULL");
  33.             return res.toString();
  34.     }
  35. }

再创建Solution类

  1. import java.util.List;
  3. public class Solution { 
  4.     public ListNode removeElements(ListNode head,int val){ 
  5.         while(head != null &&  head.val == val){ 
  6.            head = head.next;
  7.         }
  9.         if(head==null){ 
  10.             return null;
  11.         }
  13.         ListNode prev = head;
  14.         while(prev.next != null){ 
  15.             if(prev.next.val == val){ 
  16.                prev.next = prev.next.next;
  17.             }else{ 
  18.                 prev = prev.next;
  19.             }
  20.         }
  21.         return head;
  22.     }
  24.     //测试
  25.     public static void main(String[] args){ 
  26.         int[] nums = { 1,2,6,3,4,5,6,};
  27.         ListNode head = new ListNode(nums);
  28.         System.out.println(head);
  30.         ListNode res = (new Solution()).removeElements(head,6);
  31.         System.out.println(res);
  32.     }
  33. }

运行结果如下
在这里插入图片描述

3.62使用虚拟头节点

  1. public class Solution2 { 
  2.     public ListNode removeElements(ListNode head,int val){ 
  4.         ListNode dummyHead = new ListNode(-1);
  5.         dummyHead.next = head;
  7.         ListNode prev = dummyHead;
  8.         while(prev.next != null){ 
  9.             if(prev.next.val == val){ 
  10.                prev.next = prev.next.next;
  11.             }else{ 
  12.                 prev = prev.next;
  13.             }
  14.         }
  15.         return dummyHead.next;
  16.     }
  18.     //测试
  19.     public static void main(String[] args){ 
  20.         int[] nums = { 1,2,6,3,4,5,6,};
  21.         ListNode head = new ListNode(nums);
  22.         System.out.println(head);
  24.         ListNode res = (new Solution2()).removeElements(head,6);
  25.         System.out.println(res);
  26.     }
  27. }

运行结果如下
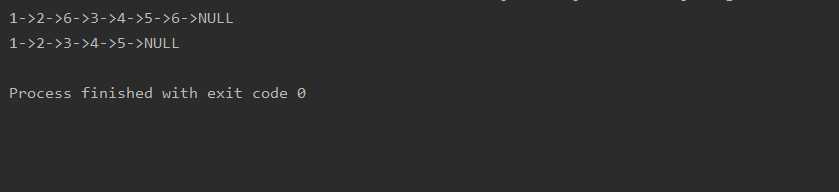
在这里插入图片描述

四、递归（Recursion）

编程语言中，函数直接或间接调用函数本身，则该函数称为递归函数。
近乎和链表相关的所有操作都可以用递归来完成。

4.1使用递归实现求和

  1. public class Sum { 
  2.     public static int sum(int[] arr){ 
  3.         return sum(arr,0);
  4.     }
  6.     //计算arr[l...n)这个区间内所有数字的和
  7.     private static int sum(int[] arr,int l){ 
  8.         if(l==arr.length){ 
  9.             return 0;
  10.         }else{ 
  11.             return arr[l] + sum(arr,l+1);
  12.         }
  13.     }
  15.     public static void main(String[] args){ 
  16.         int[] nums={ 1,2,3,4,5,6,7,8};
  17.         System.out.println(sum(nums));
  18.     }
  19. }

4.2运用递归解决链表中删除元素的问题

我们可以将最原始的链表理解成：头节点后边接着一个更短的链表，然后运用递归删除这个更短链表中相应的元素。如果头节点不需要删除的话，那么结果就是，头节点接上后面的删除元素后的那个更短的链表，如果头节点需要删除的话，那么对应的结果就是，删除元素后得道德那个更短的链表。
在这里插入图片描述
测试

  1. public class Solution3 { 
  2.     //使用递归
  3.     public ListNode removeElements(ListNode head,int val){ 
  4.         if(head == null){ 
  5.             return null;
  6.         }
  7.         head.next = removeElements(head.next,val);
  8.         return head.val == val ? head.next : head;
  9.     }
  11.     //测试
  12.     public static void main(String[] args){ 
  13.         int[] nums = { 1,2,6,3,4,5,6,};
  14.         ListNode head = new ListNode(nums);
  15.         System.out.println(head);
  17.         ListNode res = (new Solution3()).removeElements(head,6);
  18.         System.out.println(res);
  19.     }
  20. }

结果
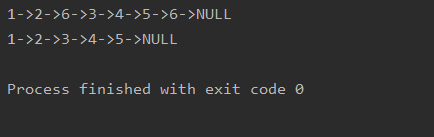
在这里插入图片描述

4.3递归算法的调试（使用打印输出的方式来了解递归调用的过程）

运用递归深度（每一个函数在它内部再次调用自身，则递归深度就多了1）来表示。

  1. import java.util.List;
  3. public class Test { 
  4.     //使用递归
  5.     public ListNode removeElements(ListNode head,int val,int depth){  //depth代表递归深度
  7.         String depthString = generateDepthString(depth);
  9.         System.out.print(depthString);//打印深度字符串
  10.         System.out.println("Call: remove" + val + "in" + head); //在head这个节点删去val这个元素
  12.         if(head == null){ 
  13.             System.out.print(depthString);
  14.             System.out.println("Return: " + head);
  15.             return head;
  16.         }
  17.         ListNode res = removeElements(head.next,val,depth+1);
  18.         System.out.print(depthString);
  19.         System.out.println("After remove" + val + ":" + res);
  21.         ListNode ret;
  22.         if(head.val == val){ 
  23.             ret = res;
  24.         }else{ 
  25.             head.next = res;
  26.             ret = head;
  27.         }
  29.         System.out.print(depthString);
  30.         System.out.println("Return: " + ret);
  31.         return ret;
  32.     }
  34.     private String generateDepthString(int depth){ 
  35.         StringBuilder res = new StringBuilder();
  36.         for(int i=0;i<depth;i++){ 
  37.             res.append("-");//深度越深，“-”越多
  38.         }
  39.         return res.toString();
  40.     }
  42.     //测试
  43.     public static void main(String[] args){ 
  44.         int[] nums = { 1,2,6,3,4,5,6,};
  45.         ListNode head = new ListNode(nums);
  46.         System.out.println(head);
  48.         ListNode res = (new Test()).removeElements(head,6,0);
  49.         System.out.println(res);
  50.     }
  51. }

运行结果如下：
-代表深度字符串，-越多代表递归调用深度越高，-的长度相同，代表在同一深度的递归调用。要在1->2->6->3->4->5->6->null这个链表中删除6，就必须递归调用对2->6->3->4->5->6->null这个链表递归调用删除6的结果，再次递归调用在6->3->4->5->6->null这个链表中删除6的结果，以此类推，当到达空列表删除6这一过程时，返回的依然为null，此时就回到了6->null这一层的结果调用，6是被删除的元素，所以此时返回的依然是null，再回到了5->6->null这一链表中删除6，返回5->null这个链表，依次返回，最终得到了最后的结果，返回1->2->3->4->5->null这一链表。
在这里插入图片描述

五、二分搜索树（Binary Search Tree）

5.1在了解二分搜索树之前，先了解一下二叉树

1.二叉树具有根节点
2.二叉树每个节点最多分成两个节点，分为左节点和右节点
3.二叉树具有天然递归结构
4.二叉树不一定是“满的”，有的节点可能只分成一个节点
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

5.2二分搜索树的特点

1.首先，二分搜索树是一个二叉树
2.二分搜索树，每个节点的值，大于其左子树的所有节点的值；小于其右子树的所有节点的值
3.每一颗子树也是二分搜索树
4.存储的元素必须右可比性

5.3二分搜索树的实现

以下程序包含了二分搜索树的增删改查等各种方法，与前面的数据结构相比
，代码量偏多，而且也相对难理解！！！不过，总体上方法都能够被调用，就是写的较乱了一些。

  1. import java.util.LinkedList;
  2. import java.util.Queue;
  3. import java.util.Stack;
  5. public class BST<E extends Comparable<E>> { 
  6.     private class Node{ 
  7.         public E e;
  8.         public Node left,right;
  10.         public Node(E e){ 
  11.             this.e = e;
  12.             left = null;
  13.             right = null;
  14.         }
  15.     }
  17.     private Node root;
  18.     private int size;
  20.     public BST(){ 
  21.         root = null;
  22.         size = 0;
  23.     }
  25.     public int size(){ 
  26.         return size;
  27.     }
  29.     public boolean isEmpty(){ 
  30.         return size==0;
  31.     }
  33.     //向二分搜索树中添加新的元素
  34.     public void add(E e){ 
  35.        root = add(root,e);
  36.     }
  38.     //向以node为根的二分搜索树中插入元素E，递归算法
  39.     //返回插入新节点后二分搜索树的根
  40.     private Node add(Node node,E e){ 
  41.         if(node == null){ 
  42.             size++;
  43.             return new Node(e);
  44.         }
  46.         if(e.compareTo(node.e) < 0){ 
  47.             node.left = add(node.left,e);
  48.         }else if(e.compareTo(node.e) > 0){ 
  49.             node.right = add(node.right,e);
  50.         }
  51.         return node;
  52.     }
  54.     //查询操作
  55.     //看二分搜索树中是否包含元素e
  56.     public boolean contains(E e){ 
  57.         return contains(root,e);
  58.     }
  60.     //看以node为根的二分搜索书中是否包含元素e，递归算法
  61.     private boolean contains(Node node,E e){ 
  62.         if(node == null){ 
  63.             return false;
  64.         }
  66.         if(e.compareTo(node.e) == 0){ 
  67.             return true;
  68.         }else if(e.compareTo(node.e) < 0){ 
  69.             return contains(node.left,e);
  70.         }else{ 
  71.             return contains(node.right,e);
  72.         }
  73.     }
  75.     //二分搜索树的前序遍历
  76.     public void preOrder(){ 
  77.         preOrder(root);
  78.     }
  80.     //前序遍历以node为根的二分搜索树，递归算法
  81.     private void preOrder(Node node){ 
  82.         if(node == null){ 
  83.             return;
  84.         }
  85.         System.out.println(node.e);
  86.         preOrder(node.left);
  87.         preOrder(node.right);
  88.     }
  90.     //二分搜索树的非递归前序遍历
  91.     public void preOrderNR(){ 
  92.         Stack<Node> stack = new Stack<>();
  93.         stack.push(root);
  94.         while(!stack.isEmpty()){ 
  95.             Node cur = stack.pop();
  96.             System.out.println(cur.e);
  98.             if(cur.right!=null){ 
  99.                 stack.push(cur.right);
  100.             }
  102.             if(cur.left!=null){ 
  103.                 stack.push(cur.left);
  104.             }
  105.         }
  106.     }
  108.     //二分搜索树的中序遍历（中序遍历的结果是顺序的）
  109.     public void inOrder(){ 
  110.         inOrder(root);
  111.     }
  113.     //中序遍历以node为根的二分搜索树，递归算法
  114.     private void inOrder(Node node){ 
  115.         if(node == null){ 
  116.             return;
  117.         }
  118.         inOrder(node.left);
  119.         System.out.println(node.e);
  120.         inOrder(node.right);
  121.     }
  123.     //二分搜索树的后序遍历
  124.     public void postOrder(){ 
  125.         postOrder(root);
  126.     }
  128.     //后续遍历以node为根的二分搜索树，递归算法
  129.     private void postOrder(Node node){ 
  130.         if(node == null){ 
  131.             return;
  132.         }
  133.         postOrder(node.left);
  134.         postOrder(node.right);
  135.         System.out.println(node.e);
  136.     }
  138.     //二分搜索树的层序遍历，运用队列
  139.     public void levelOrder(){ 
  140.         Queue<Node> q = new LinkedList<>();
  141.         q.add(root);
  142.         while(!q.isEmpty()){ 
  143.             Node cur = q.remove();
  144.             System.out.println(cur.e);
  146.             if(cur.left != null){ 
  147.                 q.add(cur.left);
  148.             }
  149.             if(cur.right != null){ 
  150.                 q.add(cur.right);
  151.             }
  152.         }
  153.     }
  155.     //寻找二分搜索树的最小元素
  156.     public E minimum(){ 
  157.         if(size == 0){ 
  158.             throw new IllegalArgumentException("BST is empty");
  159.         }
  160.         return minimum(root).e;
  161.     }
  163.     //返回以node为根的二分搜索树的最小值所在的节点
  164.     private Node minimum(Node node){ 
  165.         if(node.left == null){ 
  166.             return node;
  167.         }
  168.         return minimum(node.left);
  169.     }
  171.     //寻找二分搜索树的最大元素
  172.     public E maximum(){ 
  173.         if(size == 0){ 
  174.             throw new IllegalArgumentException("BST is empty");
  175.         }
  176.         return maximum(root).e;
  177.     }
  179.     //返回以node为根的二分搜索树的最大值所在的节点
  180.     private Node maximum(Node node){ 
  181.         if(node.right == null){ 
  182.             return node;
  183.         }
  184.         return maximum(node.right);
  185.     }
  187.     //从二分搜索树中删除最小值所在节点，返回最小值
  188.     public E removeMin(){ 
  189.         E ret = minimum();
  190.         removeMin(root);
  191.         return ret;
  192.     }
  194.     //删除掉以node为根的二分搜索树中的最小节点
  195.     //返回删除节点后的新的二分搜索树的根
  196.     private Node removeMin(Node node){ 
  197.         if(node.left == null){ 
  198.             Node rightNode = node.right;
  199.             node.right = null;
  200.             size--;
  201.             return rightNode;
  202.         }
  203.         node.left = removeMin(node.left);
  204.         return node;
  205.     }
  207.     //从二分搜索树中删除最大值所在的节点
  208.     public E removeMax(){ 
  209.         E ret = maximum();
  210.         root = removeMax(root);
  211.         return ret;
  212.     }
  214.     //删除掉以node为根的二分搜索树中的最大节点
  215.     //返回删除节点后新的二分搜索树的根
  216.     private Node removeMax(Node node){ 
  217.         if(node.right == null){ 
  218.             Node leftNode = node.left;
  219.             node.left = null;
  220.             size--;
  221.             return leftNode;
  222.         }
  223.         node.right = removeMax(node.right);
  224.         return node;
  225.     }
  227.     //从二分搜索树中删除元素为e的节点
  228.     public void remove(E e){ 
  229.         root = remove(root,e);
  230.     }
  232.     //删除以node为根的二分搜索树中值为e的节点，递归算法
  233.     //返回节点后的新的二分搜索树的根
  234.     private Node remove(Node node,E e){ 
  235.         if(node==null){ 
  236.             return null;
  237.         }
  239.         if(e.compareTo(node.e)<0){ 
  240.             node.left = remove(node.left,e);
  241.             return node;
  242.         }else if(e.compareTo(node.e)>0){ 
  243.             node.right = remove(node.right,e);
  244.             return node;
  245.         }else { 
  246.             //待删除节点左子树为空的情况
  247.             if(node.left == null){ 
  248.                 Node rightNode = node.right;
  249.                 node.right = null;
  250.                 size--;
  251.                 return rightNode;
  252.             }
  254.             //待删除节点右子树为空的情况
  255.             if(node.right == null){ 
  256.                 Node leftNode = node.left;
  257.                 node.left = null;
  258.                 size--;
  259.                 return leftNode;
  260.             }
  262.             //待删除节点左右子树均不为空的情况
  263.             //找到比待删除节点大的最小节点，即待删除节点右子树的最小节点
  264.             //用这个节点顶替待删除节点的位置
  265.             Node successor = minimum(node.right);
  266.             successor.right = removeMin(node.right);
  267.             successor.left = node.left;
  269.             node.left = node.right = null;
  270.             return successor;
  271.         }
  272.     }
  274.     @Override
  275.     public String toString(){ 
  276.         StringBuilder res = new StringBuilder();
  277.         generateBSTString(root,0,res);
  278.         return res.toString();
  279.     }
  281.     //生成以node为根节点，深度为depth的描述二叉树的字符串
  282.     private void generateBSTString(Node node,int depth,StringBuilder res){ 
  283.         if(node == null){ 
  284.             res.append(generateDepthString(depth) + "null\n");
  285.             return;
  286.         }
  288.         res.append(generateDepthString(depth) + node.e + "\n");
  289.         generateBSTString(node.left,depth+1,res);
  290.         generateBSTString(node.right,depth+1,res);
  291.     }
  293.     private String generateDepthString(int depth){ 
  294.         StringBuilder res = new StringBuilder();
  295.         for(int i=0;i<depth;i++){ 
  296.             res.append("-");
  297.         }
  298.         return res.toString();
  299.     }
  300. }

测试遍历

  1. public class Main { 
  2.     public static void main(String[] args){ 
  3.         BST<Integer> bst = new BST<>();
  4.         int[] nums = { 5,3,6,8,4,2};
  5.         for(int num:nums){ 
  6.             bst.add(num);
  7.         }
  8.         //前序遍历
  9. // bst.preOrder();
  10. // System.out.println();
  11. //
  12. // bst.preOrderNR();
  14.         //中序遍历
  15.         //bst.inOrder();
  16.         //System.out.println();
  18.         //后序遍历
  19.         //bst.postOrder();
  20.         //System.out.println();
  22.         //层序遍历
  23.         bst.levelOrder();
  24.     }
  25. }

测试删除

  1. import java.util.ArrayList;
  2. import java.util.Random;
  4. public class Main { 
  5.     public static void main(String[] args) { 
  6.         BST<Integer> bst = new BST<>();
  7.         Random random = new Random();
  9.         int n = 100;
  11.         //test removeMin
  12.         for(int i=0;i<n;i++){ 
  13.             bst.add(random.nextInt(100));
  14.         }
  15.         ArrayList<Integer> nums = new ArrayList<>();
  16.         while(!bst.isEmpty()){ 
  17.             nums.add(bst.removeMin());
  18.         }
  19.         System.out.println(nums);
  20.         for(int i=1;i<nums.size();i++){ 
  21.             if(nums.get(i-1)>nums.get(i)){ 
  22.                 throw new IllegalArgumentException("error");
  23.             }
  24.         }
  25.         System.out.println("removeMin test completed");
  27.         //test removeMax
  28.         for(int i=0;i<n;i++){ 
  29.             bst.add(random.nextInt(100));
  30.         }
  31.         nums=new ArrayList<>();
  32.         while(!bst.isEmpty()){ 
  33.             nums.add(bst.removeMax());
  34.         }
  35.         System.out.println(nums);
  36.         for(int i=1;i<nums.size();i++){ 
  37.             if(nums.get(i-1)<nums.get(i)){ 
  38.                 throw new IllegalArgumentException("error");
  39.             }
  40.         }
  41.         System.out.println("removeMax test completed");
  42.     }
  43. }

六、集合和映射（Set and Map）

6.1基于二分搜索树的集合实现

首先，要定义一个Set接口

  1. public interface Set<E> { 
  2.     void add(E e);
  3.     void remove(E e);
  4.     boolean contains(E e);
  5.     int getSize();
  6.     boolean isEmpty();
  7. }
  9. public class BSTSet<E extends Comparable<E>> implements Set<E>{ 
  11.     private BST<E> bst;
  13.     public BSTSet(){ 
  14.         bst = new BST<>();
  15.     }
  17.     @Override
  18.     public int getSize(){ 
  19.         return bst.size();
  20.     }
  22.     @Override
  23.     public boolean isEmpty(){ 
  24.         return bst.isEmpty();
  25.     }
  27.     @Override
  28.     public void add(E e){ 
  29.         bst.add(e);
  30.     }
  32.     @Override
  33.     public boolean contains(E e){ 
  34.         return bst.contains(e);
  35.     }
  37.     @Override
  38.     public void remove(E e){ 
  39.         bst.remove(e);
  40.     }
  41. }

6.2基于链表的集合实现

  1. public class LinkedListSet<E> implements Set<E> { 
  3.     private LinkedList<E> list;
  5.     public LinkedListSet(){ 
  6.         list = new LinkedList<>();
  7.     }
  9.     @Override
  10.     public int getSize(){ 
  11.         return list.getSize();
  12.     }
  14.     @Override
  15.     public boolean isEmpty(){ 
  16.         return list.isEmpty();
  17.     }
  19.     @Override
  20.     public boolean contains(E e){ 
  21.         return list.contains(e);
  22.     }
  24.     @Override
  25.     public void add(E e){ 
  26.         if(!list.contains(e)){ 
  27.             list.addFirst(e);
  28.         }
  29.     }
  31.     @Override
  32.     public void remove(E e){ 
  33.       list.removeElement(e);
  34.     }
  35. }

6.3关于映射

可以将映射简单的理解为：
字典—>单词对应相应的释意
点名册—>身份证号对应人
车辆管理—>车牌号对应车
映射特点：
1.存储键值对的数据结构（键(key)，值(value)）
2.根据键（key），寻找值（value）

6.4基于链表的映射实现

首先定义一个Map接口

  1. public interface Map<K,V> { 
  2.     void add(K key,V value);
  3.     V remove(K key);
  4.     boolean contains(K key);
  5.     V get(K key);
  6.     void set(K key, V newValue);
  7.     int getSize();
  8.     boolean isEmpty();
  9. }

创建一个LinkedListMap类

  1. public class LinkedListMap<K,V> implements Map<K,V> { 
  2.     private class Node{ 
  3.         public K key;
  4.         public V value;
  5.         public Node next;
  7.         public Node(K key,V value,Node next){ 
  8.             this.key = key;
  9.             this.value = value;
  10.             this.next = next;
  11.         }
  13.         public Node(K key){ 
  14.             this(key,null,null);
  15.         }
  17.         public Node(){ 
  18.             this(null,null,null);
  19.         }
  21.         @Override
  22.         public String toString(){ 
  23.             return key.toString() + ":" + value.toString();
  24.         }
  25.     }
  27.         private Node dummyHead;
  28.         private int size;
  30.         public LinkedListMap(){ 
  31.             dummyHead = new Node();
  32.             size = 0;
  33.         }
  35.         @Override
  36.         public int getSize(){ 
  37.             return size;
  38.         }
  40.         @Override
  41.         public boolean isEmpty(){ 
  42.             return size==0;
  43.         }
  45.         private Node getNode(K key){ 
  46.             Node cur = dummyHead.next;
  47.             while(cur!=null){ 
  48.                 if(cur.key.equals(key)){ 
  49.                     return cur;
  50.                 }
  51.                 cur = cur.next;
  52.             }
  53.             return null;
  54.         }
  56.         @Override
  57.         public boolean contains(K key){ 
  58.             return getNode(key) != null;
  59.         }
  61.         @Override
  62.         public V get(K key){ 
  63.             Node node = getNode(key);
  64.             return node == null ? null : node.value;
  65.         }
  67.         //添加操作
  68.         @Override
  69.         public void add(K key, V value){ 
  70.             Node node = getNode(key);
  71.             if(node == null){ 
  72.                 dummyHead.next = new Node(key,value,dummyHead.next);
  73.                 size++;
  74.             }else{ 
  75.                 node.value = value;
  76.             }
  77.         }
  79.         @Override
  80.         public void set(K key, V newValue){ 
  81.             Node node = getNode(key);
  82.             if(node == null){ 
  83.                 throw new IllegalArgumentException(key + "doesn't exist ");
  84.             }
  85.             node.value = newValue;
  86.         }
  88.         @Override
  89.         public V remove(K key){ 
  90.             Node prev = dummyHead;
  91.             while(prev.next != null){ 
  92.                 if(prev.next != null){ 
  93.                     break;
  94.                 }
  95.                 prev = prev.next;
  96.             }
  97.             if(prev.next != null){ 
  98.                 Node delNode = prev.next;
  99.                 prev.next = delNode.next;
  100.                 delNode.next = null;
  101.                 size--;
  102.                 return delNode.value;
  103.             }
  104.             return null;
  105.         }
  106. }

6.5基于二分搜索树的映射实现

  1. public class BSTMap<K extends Comparable<K>,V> implements Map<K,V>{ 
  3.     private class Node{ 
  4.         public K key;
  5.         public V value;
  6.         public Node left,right;
  8.         public Node(K key,V value){ 
  9.             this.key=key;
  10.             this.value=value;
  11.             left=null;
  12.             right=null;
  13.         }
  14.     }
  16.     private Node root;
  17.     private int size;
  19.     public BSTMap(){ 
  20.         root=null;
  21.         size=0;
  22.     }
  24.     @Override
  25.     public int getSize(){ 
  26.         return size;
  27.     }
  29.     @Override
  30.     public boolean isEmpty(){ 
  31.         return size==0;
  32.     }
  34.     //向二分搜索树中添加新的元素（key ，value）
  35.     @Override
  36.     public void add(K key,V value){ 
  37.         root = add(root,key,value);
  38.     }
  40.     //向node为根的二分搜索树中插入元素（key，value）,递归算法
  41.     //返回插入新节点后二分搜索树的根
  42.     private Node add(Node node,K key,V value){ 
  43.         if(node == null){ 
  44.             size++;
  45.             return new Node(key,value);
  46.         }
  47.         if(key.compareTo(node.key)<0){ 
  48.             node.left = add(node.left,key,value);
  49.         }else if(key.compareTo(node.key)>0){ 
  50.             node.right = add(node.right,key,value);
  51.         }else if(key.compareTo(node.key)==0){ 
  52.             node.value=value;
  53.         }
  54.         return node;
  55.     }
  57.     //返回以node为节点的二分搜索树中，key所在的节点
  58.     private Node getNode(Node node,K key){ 
  59.         if(node==null){ 
  60.             return null;
  61.         }
  62.         if(key.compareTo(node.key)==0){ 
  63.             return node;
  64.         }else if(key.compareTo(node.key)<0){ 
  65.             return getNode(node.left,key);
  66.         }else
  67.             return getNode(node.right,key);
  68.     }
  70.     @Override
  71.     public boolean contains(K key){ 
  72.         return getNode(root,key) != null;
  73.     }
  75.     @Override
  76.     public V get(K key){ 
  77.         Node node=getNode(root,key);
  78.         return node == null? null : node.value;
  79.     }
  81.     @Override
  82.     public void set(K key,V newValue){ 
  83.         Node node = getNode(root,key);
  84.         if(node == null){ 
  85.             throw new IllegalArgumentException(key + "doesn't exist");
  86.         }
  87.         node.value = newValue;
  88.     }
  90.     //返回以node为根的二分搜索树的最小值所在的节点
  91.     private Node minimum(Node node){ 
  92.         if(node.left==null){ 
  93.             return node;
  94.         }
  95.         return minimum(node.left);
  96.     }
  98.     //删除掉以node为根的二分搜索树中的最小节点
  99.     //返回删除节点后新的二分搜索树的根
  100.     private Node removeMin(Node node){ 
  101.         if(node.left == null){ 
  102.             Node rightNode = node.right;
  103.             node.right=null;
  104.             size--;
  105.             return rightNode;
  106.         }
  107.         node.left = removeMin(node.left);
  108.         return node;
  109.     }
  111.     //从二分搜索树中删除键为key的节点
  112.     @Override
  113.     public V remove(K key){ 
  114.         Node node = getNode(root,key);
  115.         if(node != null){ 
  116.             root = remove(root,key);
  117.             return node.value;
  118.         }
  119.         return null;
  120.     }
  122.     //删除掉以node为根的二分搜索树中键为key的节点，递归算法
  123.     //返回删除节点后新的二分搜索树的根
  124.     private Node remove(Node node,K key){ 
  125.         if(node==null){ 
  126.             return null;
  127.         }
  128.         if(key.compareTo(node.key)<0){ 
  129.             node.left = remove(node.left,key);
  130.             return node;
  131.         }else if(key.compareTo(node.key)>0){ 
  132.             node.right = remove(node.right,key);
  133.             return node;
  134.         }else{  //key.compareTo(node.key)==0
  135.             //删除节点左子树为空的情况
  136.             if(node.left == null){ 
  137.                 Node rightNode = node.right;
  138.                 node.right = null;
  139.                 size--;
  140.                 return rightNode;
  141.             }
  142.             //删除节点右子树为空的情况
  143.             if(node.right == null){ 
  144.                 Node leftNode = node.left;
  145.                 node.left = null;
  146.                 size--;
  147.                 return leftNode;
  148.             }
  149.             //待删除节点左右子树均不为空的情况
  150.             //找到比待删除节点大的最小节点，即待删除节点右子树的最小节点
  151.             //用这个节点顶替待删除节点的位置
  152.             Node successor = minimum(node.right);
  153.             successor.right = removeMin(node.right);
  154.             successor.left = node.left;
  155.             node.left = node.right = null;
  156.             return successor;
  157.         }
  158.     }
  159. }

七、优先队列（PriorityQueue）和堆(Heap)

优先队列：出队顺序和入队顺序无关；和优先级相关。可以简单的理解为，医院中，医生会根据患者生病的程度大小来进行手术，较为严重的患者，相对来说，优先级更高一些，所以医生会对他先进行手术。

7.1使用二叉树来表示堆，简称二叉堆

1.二叉堆是一棵完全二叉树(将元素按一层一层的顺序排列成树的形状)
2.二叉堆中某个节点的值总是不大于其父亲节点的值，称其为最大堆
3.满二叉树就是除了叶子节点，左右孩子都不为空
4.完全二叉树不一定是一个满的二叉树，缺失节点的那一部分一定是整棵树的右下侧

在这里插入图片描述

7.2利用数组实现最大堆

  1. import java.util.IllformedLocaleException;
  3. public class MaxHeap<E extends Comparable<E>> { 
  5.     private Array<E> data;
  7.     public MaxHeap(int capacity){ 
  8.         data = new Array<>(capacity);
  9.     }
  11.     public MaxHeap(){ 
  12.         data = new Array<>();
  13.     }
  15.     //将任意数组整理成堆的形状
  16.     public MaxHeap(E[] arr){ 
  17.         data = new Array<>(arr);
  18.         for(int i = parent(arr.length-1);i>=0;i--){ 
  19.             siftDown(i);
  20.         }
  21.     }
  23.     //返回堆中的元素个数
  24.     public int size(){ 
  25.         return data.getSize();
  26.     }
  28.     //返回一个布尔值，表示堆中是否为空
  29.     public boolean isEmpty(){ 
  30.         return data.isEmpty();
  31.     }
  33.     //返回完全二叉树的数组表示中，一个索引所表示的元素的父亲节点的索引
  34.     private int parent(int index){ 
  35.         if(index==0){ 
  36.             throw new IllegalArgumentException("index-0 doesn't have parent");
  37.         }
  38.         return (index-1)/2;
  39.     }
  41.     //返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
  42.     private int leftChild(int index){ 
  43.         return index*2+1;
  44.     }
  46.     //返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
  47.     private int rightChild(int index){ 
  48.         return index*2+2;
  49.     }
  51.     //向堆中添加元素
  52.     public void add(E e){ 
  53.         data.addLast(e);
  54.         siftUp(data.getSize()-1);
  55.     }
  57.     //上移元素
  58.     private void siftUp(int k){ 
  59.         while(k>0 && data.get(parent(k)).compareTo(data.get(k))<0){ 
  60.             data.swap(k,parent(k));
  61.             k=parent(k);
  62.         }
  63.     }
  65.     //看堆中的最大元素
  66.     public E findMax(){ 
  67.         if(data.getSize() == 0){ 
  68.             throw new IllformedLocaleException("heap is empty");
  69.         }
  70.         return data.get(0);
  71.     }
  73.     //取出堆中最大元素
  74.     public E extractMax(){ 
  75.         E ret = findMax();
  76.         data.swap(0,data.getSize()-1);
  77.         data.removeLast();
  78.         siftDown(0);
  79.         return ret;
  80.     }
  82.     //向下移动
  83.     private void siftDown(int k){ 
  84.         while(leftChild(k)<data.getSize()){ 
  85.             int j = leftChild(k);
  86.             if(j+1 < data.getSize() && data.get(j+1).compareTo(data.get(j))>0){ 
  87.                 j = rightChild(k);
  88.                 //data[j]是leftChild和rightChild中的最大值
  89.             }
  90.             if(data.get(k).compareTo(data.get(j))>=0){ 
  91.                 break;
  92.             }
  93.             data.swap(k,j);
  94.             k=j;
  95.         }
  96.     }
  98.     //取出堆中的最大元素，并且替换成元素e
  99.     public E replace(E e){ 
  100.         E ret = findMax();
  101.         data.set(0,e);
  102.         return ret;
  103.     }
  104. }

测试用Heapify与不用Heapify的性能差别

  1. import java.util.Random;
  3. public class Main { 
  4.     private static double testHeap(Integer[] testData,boolean isHeapify){ 
  5.         long startTime = System.nanoTime();
  7.         MaxHeap<Integer> maxHeap;
  8.         if(isHeapify){ 
  9.             maxHeap = new MaxHeap<>(testData);
  10.         }else{ 
  11.             maxHeap = new MaxHeap<>();
  12.             for(int num: testData){ 
  13.                 maxHeap.add(num);
  14.             }
  15.         }
  17.         int[] arr = new int[testData.length];
  18.         for(int i=0;i<testData.length;i++){ 
  19.             arr[i] = maxHeap.extractMax();
  20.         }
  22.         for(int i=1;i<testData.length;i++){ 
  23.             if(arr[i-1]<arr[i]){ 
  24.                 throw new IllegalArgumentException("Error");
  25.             }
  26.         }
  27.         System.out.println("Test MaxHeap completed");
  29.         long endTime = System.nanoTime();
  30.         return (endTime-startTime)/1000000000.0;
  31.     }
  33.     public static void main(String[] args){ 
  34.         int n=1000000;
  35.         Random random = new Random();
  36.         Integer[] testData = new Integer[n];
  37.         for(int i=0;i<n;i++){ 
  38.            testData[i] = random.nextInt(Integer.MAX_VALUE);
  39.         }
  41.         double time1 = testHeap(testData,false);
  42.         System.out.println("Without heapify: " +time1+ "s");
  44.         double time2 = testHeap(testData,true);
  45.         System.out.println("With heapify: " +time2+ "s");
  47.     }
  48. }

测试结果：
用了Heapify（将任意数组整理成堆的形状）的耗时短一些
在这里插入图片描述

7.3基于堆的优先队列

  1. public class PriorityQueue<E extends Comparable<E>> implements Queue<E> { 
  2.     private MaxHeap<E> maxHeap;
  3.     public PriorityQueue(){ 
  4.         maxHeap = new MaxHeap<>();
  5.     }
  7.     @Override
  8.     public int getSize(){ 
  9.         return maxHeap.size();
  10.     }
  12.     @Override
  13.     public boolean isEmpty(){ 
  14.         return maxHeap.isEmpty();
  15.     }
  17.     @Override
  18.     public E getFront(){ 
  19.         return maxHeap.findMax();
  20.     }
  22.     //入队
  23.     @Override
  24.     public void enqueue(E e){ 
  25.         maxHeap.add(e);
  26.     }
  28.     //出队
  29.     @Override
  30.     public E dequeue(){ 
  31.         return maxHeap.extractMax();
  32.     }
  33. }

八、线段树(Segment Tree)、区间树

8.1关于线段树

线段树就是对每一棵二叉树的每一个节点存储的是一个线段或者是一个区间相应的信息。
1.线段树不一定是满二叉树，也不一定是完全二叉树
2.线段树是平衡二叉树(对于整棵树来说，最大的深度和最小的深度他们之间的差最多只有可能为1)
在这里插入图片描述

8.2实现线段树

创建merger接口

  1. public interface Merger<E> { 
  2.     E merge(E a,E b);
  3. }

创建线段树类

  1. package _SegmentTree;
  3. import java.lang.management.BufferPoolMXBean;
  5. public class SegmentTree<E> { 
  6.     private E[] tree;
  7.     private E[] data;
  8.     private Merger<E> merger;
  10.     public SegmentTree(E[] arr,Merger<E> merger){ 
  11.         this.merger=merger;
  12.         data =(E[]) new Object[arr.length];
  13.         for(int i=0;i<arr.length;i++){ 
  14.             data[i]=arr[i];
  15.         }
  16.         tree =(E[]) new Object[4*arr.length];
  17.         buildSegmentTree(0,0,data.length-1);
  18.     }
  20.     //在treeIndex的位置创建表示区间[l...r]的线段树
  21.     private void buildSegmentTree(int treeIndex,int l,int r){ 
  22.         if(l==r){ 
  23.             tree[treeIndex] = data[l];
  24.             return;
  25.         }
  27.         int leftTreeIndex = leftChild(treeIndex);
  28.         int rightTreeIndex = rightChild(treeIndex);
  30.         int mid = l + (r-l)/2;
  31.         buildSegmentTree(leftTreeIndex,l,mid);
  32.         buildSegmentTree(rightTreeIndex,mid+1,r);
  33.         tree[treeIndex] = merger.merge(tree[leftTreeIndex] , tree[rightTreeIndex]);
  34.     }
  37.     public int getSize(){ 
  38.         return data.length;
  39.     }
  41.     public E get(int index){ 
  42.         if(index<0 || index>=data.length){ 
  43.             throw new IllegalArgumentException("Index is illegal");
  44.         }
  45.         return data[index];
  46.     }
  48.     //返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
  49.     private int leftChild(int index){ 
  50.         return 2*index + 1;
  51.     }
  53.     //返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
  54.     private int rightChild(int index){ 
  55.         return 2*index + 2;
  56.     }
  58.     //返回区间[queryL，queryR]的值（求和过程）
  59.     public E query(int queryL,int queryR){ 
  60.         if(queryL<0 || queryL >=data.length || queryR <0 || queryR >=data.length || queryL > queryR){ 
  61.             throw new IllegalArgumentException("index is illegal");
  62.         }
  63.         return query(0,0,data.length-1,queryL,queryR);
  64.     }
  66.     //在一treeID为根的线段树中[l...r]的范围里，搜索区间[queryL...queryR]的值
  67.     private E query(int treeIndex,int l,int r,int queryL,int queryR){ 
  68.         if(l==queryL && r==queryR){ 
  69.             return tree[treeIndex];
  70.         }
  71.         int mid = l+(r-l)/2;
  72.         int leftTreeIndex=leftChild(treeIndex);
  73.         int rightTreeIndex=rightChild(treeIndex);
  75.         if(queryL >= mid+1){ 
  76.             return query(rightTreeIndex,mid+1,r,queryL,queryR);
  77.         }else if(queryR <= mid){ 
  78.             return query(leftTreeIndex,l,mid,queryL,queryR);
  79.         }
  81.         E leftResult = query(leftTreeIndex,l,mid,queryL,mid);
  82.         E rightResult = query(rightTreeIndex,mid+1,r,mid+1,queryR);
  83.         return merger.merge(leftResult,rightResult);
  84.     }
  86.     //将index位置的值，跟新为e
  87.     public void set(int index,E e){ 
  88.         if(index < 0 || index >= data.length){ 
  89.             throw new IllegalArgumentException("Index is illegal");
  90.         }
  91.         data[index] = e;
  92.         set(0,0,data.length-1,index,e);
  93.     }
  95.     //在以treeIndex为根的线段树中跟新index的值为e
  96.     private void set(int treeIndex,int l,int r,int index,E e){ 
  97.         if(l==r){ 
  98.             tree[treeIndex] = e;
  99.             return;
  100.         }
  101.         int mid = l+(r-l)/2;
  102.         int leftTreeIndex = leftChild(treeIndex);
  103.         int rightTreeIndex = rightChild(treeIndex);
  104.         if(index >= mid + 1){ 
  105.             set(rightTreeIndex,mid+1,r,index,e);
  106.         }else{   //index<=mid
  107.             set(leftTreeIndex,l,mid,index,e);
  108.         }
  109.         tree[treeIndex]=merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
  110.     }
  112.     @Override
  113.     public String toString(){ 
  114.         StringBuilder res = new StringBuilder();
  115.         res.append('[');
  116.         for(int i=0;i<tree.length;i++){ 
  117.             if(tree[i] != null){ 
  118.                 res.append(tree[i]);
  119.             }else{ 
  120.                 res.append("null");
  121.             }
  122.             if(i != tree.length-1){ 
  123.                 res.append(',');
  124.             }
  125.         }
  126.         res.append(']');
  127.         return res.toString();
  128.     }
  129. }

测试求和

  1. package _SegmentTree;
  3. public class Main { 
  4.     public static void main(String[] args){ 
  5.         Integer[] nums = { -2,0,3,-5,2,-1};
  6.         SegmentTree<Integer> segTree = new SegmentTree<>(nums,(a,b) -> a+b);
  8.         System.out.println(segTree.query(0,2)); //index从0-2的元素的和
  9.     }
  10. }

输出结果
在这里插入图片描述

九、字典树(Trie),也叫做前缀树

可以将字典树简单的理解为字典，从而去查询对应节点所指的对应元素，从而找出所对应的单词。
在这里插入图片描述

9.1字典树的实现

字典树的实现主要用于处理一些字符串问题！

  1. package _Trie;
  3. import java.util.TreeMap;
  5. public class Trie { 
  7.     private class Node{ 
  9.         public boolean isWord;
  10.         public TreeMap<Character,Node> next;
  12.         public Node(boolean isWord){ 
  13.             this.isWord=isWord;
  14.             next = new TreeMap<>();
  15.         }
  17.         public Node(){ 
  18.             this(false);
  19.         }
  20.     }
  22.     private Node root;
  23.     private int size;
  25.     public Trie(){ 
  26.         root = new Node();
  27.         size = 0;
  28.     }
  30.     //获得Trie中存储的单词数量
  31.     public int getSize(){ 
  32.         return size;
  33.     }
  35.     //向Trie中添加一个新的单词word
  36.     public void add(String word){ 
  37.         Node cur = root;
  38.         for(int i=0;i<word.length();i++){ 
  39.             char c = word.charAt(i);
  40.             if(cur.next.get(c) == null){ 
  41.                 cur.next.put(c,new Node());
  42.             }
  43.             cur = cur.next.get(c);
  44.         }
  45.         if(!cur.isWord){ 
  46.             cur.isWord=true;
  47.             size++;
  48.         }
  49.     }
  51.     //查询单词word是否在Trie中
  52.     public boolean contains(String word){ 
  53.         Node cur = root;
  54.         for(int i=0;i<word.length();i++){ 
  55.             char c = word.charAt(i);
  56.             if(cur.next.get(c) == null){ 
  57.                 return false;
  58.             }
  59.             cur = cur.next.get(c);
  60.         }
  61.         return cur.isWord;
  62.     }
  64.     //前缀查询
  65.     //查询是否在Trie中有单词以prefix为前缀
  66.     public boolean isPrefix(String prefix){ 
  67.         Node cur = root;
  68.         for(int i=0;i<prefix.length();i++){ 
  69.             char c=prefix.charAt(i);
  70.             if(cur.next.get(c)==null){ 
  71.                 return false;
  72.             }
  73.             cur =cur.next.get(c);
  74.         }
  75.         return true;
  76.     }
  77. }

十、并查集（Union Find）

由孩子指向父亲的树形结构，用来处理连接问题(判断节点间的连接状态)。

10.1数组模拟实现并查集

  1. package _UnionFind;
  2. //第一版的Union-Find
  3. public class UnionFind1 implements UF{ 
  5.     private  int[] id;
  7.     public UnionFind1(int size){ 
  8.         id=new int[size];
  9.         for(int i=0;i<id.length;i++){ 
  10.             id[i]=i;
  11.         }
  12.     }
  14.     @Override
  15.     public int getSize(){ 
  16.         return id.length;
  17.     }
  19.     //查找元素p所对应的集合编号
  20.     private int find(int p){ 
  21.         if(p<0 && p>= id.length){ 
  22.             throw new IllegalArgumentException("p is out of bound");
  23.         }
  24.         return id[p];
  25.     }
  27.     //查看元素p和元素q是否所属一个集合
  28.     @Override
  29.     public boolean isConnected(int p,int q){ 
  30.         return find(p) == find(q);
  31.     }
  33.     //合并元素p和元素q所属的集合
  34.     @Override
  35.     public void unionElements(int p,int q){ 
  36.         int pID = find(p);
  37.         int qID = find(q);
  39.         if(pID == qID){ 
  40.             return;
  41.         }
  43.         for(int i=0;i<id.length;i++){ 
  44.             if(id[i]==pID){ 
  45.                 id[i]=qID;
  46.             }
  47.         }
  48.     }
  49. }

10.2用孩子指向树的结构实现并查集

在这里插入图片描述

  1. package _UnionFind;
  2. //第二版并查集
  3. public class UnionFind2 implements UF { 
  5.     private int[] parent;
  7.     public UnionFind2(int size){ 
  8.         parent = new int[size];
  10.         for(int i=0;i<size;i++){ 
  11.             parent[i] = i;  //节点初始化，让每个节点都指向自身
  12.         }
  13.     }
  15.     @Override
  16.     public int getSize(){ 
  17.         return parent.length;
  18.     }
  20.     //查找过程，查找元素p所对应的集合编号
  21.     //O(h)复杂度，h为树的高度
  22.     private int find(int p){ 
  23.         if(p<0 && p>= parent.length){ 
  24.             throw new IllegalArgumentException("p is out of bound");
  25.         }
  26.         while (p != parent[p]){ 
  27.             p = parent[p];
  28.         }
  29.         return p;
  30.     }
  32.     //产看元素p和元素q是否所属一个集合
  33.     //O(h)复杂度，h为树的高度
  34.     @Override
  35.     public boolean isConnected(int p,int q){ 
  36.         return find(p) == find(q);
  37.     }
  39.     //合并元素p和合并元素q所属的集合
  40.     //O(h)复杂度，h为树的高度
  41.     @Override
  42.     public void unionElements(int p,int q){ 
  43.         int pRoot = find(p);
  44.         int qRoot = find(q);
  46.         if(pRoot == qRoot){ 
  47.             return;
  48.         }
  49.         parent[pRoot] = qRoot;
  50.     }
  51. }

10.3基于size的优化

  1. package _UnionFind;
  2. //第三版并查集
  3. public class UnionFind3 implements UF { 
  5.     private int[] parent;
  6.     private int[] sz;   //sz[i]表示以i为根的集合中元素个数
  8.     public UnionFind3(int size){ 
  9.         parent = new int[size];
  10.         sz = new int[size];
  12.         for(int i=0;i<size;i++){ 
  13.             parent[i] = i;  //节点初始化，让每个节点都指向自身
  14.             sz[i] = 1;
  15.         }
  16.     }
  18.     @Override
  19.     public int getSize(){ 
  20.         return parent.length;
  21.     }
  23.     //查找过程，查找元素p所对应的集合编号
  24.     //O(h)复杂度，h为树的高度
  25.     private int find(int p){ 
  26.         if(p<0 && p>= parent.length){ 
  27.             throw new IllegalArgumentException("p is out of bound");
  28.         }
  29.         while (p != parent[p]){ 
  30.             p = parent[p];
  31.         }
  32.         return p;
  33.     }
  35.     //产看元素p和元素q是否所属一个集合
  36.     //O(h)复杂度，h为树的高度
  37.     @Override
  38.     public boolean isConnected(int p,int q){ 
  39.         return find(p) == find(q);
  40.     }
  42.     //合并元素p和合并元素q所属的集合
  43.     //O(h)复杂度，h为树的高度
  44.     @Override
  45.     public void unionElements(int p,int q) { 
  46.         int pRoot = find(p);
  47.         int qRoot = find(q);
  49.         if (pRoot == qRoot) { 
  50.             return;
  51.         }
  53.         //根据两个元素所在树的元素个数不同判断合并方向
  54.         //将元素个数少的集合合并到元素个数多的集合上
  55.         if (sz[pRoot] < sz[qRoot]) { 
  56.             parent[pRoot] = qRoot;
  57.             sz[qRoot] += sz[pRoot];
  58.         }else{   //sz[qRoot] <= sz[pRoot]
  59.             parent[qRoot] = pRoot;
  60.             sz[pRoot] += sz[qRoot];
  61.         }
  62.     }
  63. }

10.4基于rank(指树的高度)的优化

让节点树高度低的指向节点树高度高的
在这里插入图片描述

  1. package _UnionFind;
  2. //第四版并查集
  3. public class UnionFind4 implements UF { 
  5.     private int[] parent;
  6.     private int[] rank;   //rank[i]表示以i为根的集合所表示的树的层数
  8.     public UnionFind4(int size){ 
  9.         parent = new int[size];
  10.         rank = new int[size];
  12.         for(int i=0;i<size;i++){ 
  13.             parent[i] = i;  //节点初始化，让每个节点都指向自身
  14.             rank[i] = 1;    //节点层数为1
  15.         }
  16.     }
  18.     @Override
  19.     public int getSize(){ 
  20.         return parent.length;
  21.     }
  23.     //查找过程，查找元素p所对应的集合编号
  24.     //O(h)复杂度，h为树的高度
  25.     private int find(int p){ 
  26.         if(p<0 && p>= parent.length){ 
  27.             throw new IllegalArgumentException("p is out of bound");
  28.         }
  29.         while (p != parent[p]){ 
  30.             p = parent[p];
  31.         }
  32.         return p;
  33.     }
  35.     //产看元素p和元素q是否所属一个集合
  36.     //O(h)复杂度，h为树的高度
  37.     @Override
  38.     public boolean isConnected(int p,int q){ 
  39.         return find(p) == find(q);
  40.     }
  42.     //合并元素p和合并元素q所属的集合
  43.     //O(h)复杂度，h为树的高度
  44.     @Override
  45.     public void unionElements(int p,int q) { 
  46.         int pRoot = find(p);
  47.         int qRoot = find(q);
  49.         if (pRoot == qRoot) { 
  50.             return;
  51.         }
  53.         //根据两个元素所在树的rank不同判断合并方向
  54.         //将rank低的集合合并到rank高的集合上
  55.         if (rank[pRoot] < rank[qRoot]) { 
  56.             parent[pRoot] = qRoot;
  57.         }else if(rank[qRoot] < rank[pRoot]){ 
  58.             parent[qRoot] = pRoot;
  59.         }else{   //RANK[qRoot] == rank[pRoot]
  60.             parent[qRoot] = pRoot;
  61.             rank[pRoot] += 1;
  62.         }
  63.     }
  64. }

10.5路径压缩

在这里插入图片描述

  1. package _UnionFind;
  2. //第五版并查集
  3. public class UnionFind5 implements UF { 
  5.     private int[] parent;
  6.     private int[] rank;   //rank[i]表示以i为根的集合所表示的树的层数
  8.     public UnionFind5(int size){ 
  9.         parent = new int[size];
  10.         rank = new int[size];
  12.         for(int i=0;i<size;i++){ 
  13.             parent[i] = i;  //节点初始化，让每个节点都指向自身
  14.             rank[i] = 1;    //节点层数为1
  15.         }
  16.     }
  18.     @Override
  19.     public int getSize(){ 
  20.         return parent.length;
  21.     }
  23.     //查找过程，查找元素p所对应的集合编号
  24.     //O(h)复杂度，h为树的高度
  25.     private int find(int p){ 
  26.         if(p<0 && p>= parent.length){ 
  27.             throw new IllegalArgumentException("p is out of bound");
  28.         }
  29.         while (p != parent[p]){ 
  30.             parent[p] = parent[parent[p]];
  31.             p = parent[p];
  32.         }
  33.         return p;
  34.     }
  36.     //产看元素p和元素q是否所属一个集合
  37.     //O(h)复杂度，h为树的高度
  38.     @Override
  39.     public boolean isConnected(int p,int q){ 
  40.         return find(p) == find(q);
  41.     }
  43.     //合并元素p和合并元素q所属的集合
  44.     //O(h)复杂度，h为树的高度
  45.     @Override
  46.     public void unionElements(int p,int q) { 
  47.         int pRoot = find(p);
  48.         int qRoot = find(q);
  50.         if (pRoot == qRoot) { 
  51.             return;
  52.         }
  54.         //根据两个元素所在树的rank不同判断合并方向
  55.         //将rank低的集合合并到rank高的集合上
  56.         if (rank[pRoot] < rank[qRoot]) { 
  57.             parent[pRoot] = qRoot;
  58.         }else if(rank[qRoot] < rank[pRoot]){ 
  59.             parent[qRoot] = pRoot;
  60.         }else{   //RANK[qRoot] == rank[pRoot]
  61.             parent[qRoot] = pRoot;
  62.             rank[pRoot] += 1;
  63.         }
  64.     }
  65. }

在这里插入图片描述

  1. package _UnionFind;
  2. //第六版并查集
  3. public class UnionFind6 implements UF { 
  5.     private int[] parent;
  6.     private int[] rank;   //rank[i]表示以i为根的集合所表示的树的层数
  8.     public UnionFind6(int size){ 
  9.         parent = new int[size];
  10.         rank = new int[size];
  12.         for(int i=0;i<size;i++){ 
  13.             parent[i] = i;  //节点初始化，让每个节点都指向自身
  14.             rank[i] = 1;    //节点层数为1
  15.         }
  16.     }
  18.     @Override
  19.     public int getSize(){ 
  20.         return parent.length;
  21.     }
  23.     //查找过程，查找元素p所对应的集合编号
  24.     //O(h)复杂度，h为树的高度
  25.     private int find(int p){ 
  26.         if(p<0 && p>= parent.length){ 
  27.             throw new IllegalArgumentException("p is out of bound");
  28.         }
  29.         if(p != parent[p]){ 
  30.             parent[p] = find(parent[p]);
  31.         }
  32.         return parent[p];
  33.     }
  35.     //产看元素p和元素q是否所属一个集合
  36.     //O(h)复杂度，h为树的高度
  37.     @Override
  38.     public boolean isConnected(int p,int q){ 
  39.         return find(p) == find(q);
  40.     }
  42.     //合并元素p和合并元素q所属的集合
  43.     //O(h)复杂度，h为树的高度
  44.     @Override
  45.     public void unionElements(int p,int q) { 
  46.         int pRoot = find(p);
  47.         int qRoot = find(q);
  49.         if (pRoot == qRoot) { 
  50.             return;
  51.         }
  53.         //根据两个元素所在树的rank不同判断合并方向
  54.         //将rank低的集合合并到rank高的集合上
  55.         if (rank[pRoot] < rank[qRoot]) { 
  56.             parent[pRoot] = qRoot;
  57.         }else if(rank[qRoot] < rank[pRoot]){ 
  58.             parent[qRoot] = pRoot;
  59.         }else{   //RANK[qRoot] == rank[pRoot]
  60.             parent[qRoot] = pRoot;
  61.             rank[pRoot] += 1;
  62.         }
  63.     }
  64. }

测试性能

  1. package _UnionFind;
  3. import java.util.Random;
  5. public class Main { 
  7.     private static double testUF(UF uf,int m){ 
  8.         int size = uf.getSize();
  9.         Random random = new Random();
  11.         long startTime = System.nanoTime();
  13.         for(int i=0;i<m;i++){ 
  14.             int a = random.nextInt(size);
  15.             int b = random.nextInt(size);
  16.             uf.unionElements(a,b);
  17.         }
  19.         for(int i=0;i<m;i++){ 
  20.             int a = random.nextInt(size);
  21.             int b = random.nextInt(size);
  22.             uf.isConnected(a,b);
  23.         }
  25.         long endTime = System.nanoTime();
  26.         return (endTime-startTime)/1000000000.0;
  27.     }
  29.     public static void main(String[] args){ 
  30.         int size = 100000;
  31.         int m = 100000;
  33.         UnionFind1 uf1 = new UnionFind1(size);
  34.         System.out.println("UnionFind1 :" +testUF(uf1,m) + "s");
  36.         UnionFind2 uf2 = new UnionFind2(size);
  37.         System.out.println("UnionFind2 :" +testUF(uf2,m) + "s");
  39.         UnionFind3 uf3 = new UnionFind3(size);
  40.         System.out.println("UnionFind3 :" +testUF(uf3,m) + "s");
  42.         UnionFind4 uf4 = new UnionFind4(size);
  43.         System.out.println("UnionFind4 :" +testUF(uf4,m) + "s");
  45.         UnionFind5 uf5 = new UnionFind5(size);
  46.         System.out.println("UnionFind5 :" +testUF(uf5,m) + "s");
  48.         UnionFind6 uf6 = new UnionFind6(size);
  49.         System.out.println("UnionFind6 :" +testUF(uf6,m) + "s");
  50.     }
  51. }

测试结果
可以将size和m继续增大，效果可能会明显一些
在这里插入图片描述

十一、AVL树、平衡二叉树

1.平衡二叉树：对于任意一个节点，左子树和右子树的高度差不能超过1
2.平衡因子：任意节点而言，左右子树高度差，计算高度差用左子树的高度减去右子树的高度
在这里插入图片描述

11.1AVL树的实现

以下代码实现了AVL树，计算节点的高度和平衡因子，以及AVL的删除元素，以及左右旋转的实现

  1. package _AVLTree;
  3. import _Map.Map;
  5. import java.util.ArrayList;
  7. public class AVLTree<K extends Comparable<K>,V> implements Map<K,V>{ 
  9.     private class Node{ 
  10.         public K key;
  11.         public V value;
  12.         public Node left,right;
  13.         public int height;
  15.         public Node(K key,V value){ 
  16.             this.key=key;
  17.             this.value=value;
  18.             left=null;
  19.             right=null;
  20.             height=1;
  21.         }
  22.     }
  24.     private Node root;
  25.     private int size;
  27.     public AVLTree(){ 
  28.         root=null;
  29.         size=0;
  30.     }
  32.     @Override
  33.     public int getSize(){ 
  34.         return size;
  35.     }
  37.     @Override
  38.     public boolean isEmpty(){ 
  39.         return size==0;
  40.     }
  42.     //判断该二叉树是否是二分搜索树
  43.     public boolean isBST(){ 
  44.         ArrayList<K> keys = new ArrayList<>();
  45.         inOrder(root,keys);
  46.         for(int i=1;i<keys.size();i++){ 
  47.             if(keys.get(i-1).compareTo(keys.get(i)) > 0){ 
  48.                 return false;
  49.             }
  50.         }
  51.         return true;
  52.     }
  54.     private void inOrder(Node node,ArrayList<K> keys){ 
  55.         if(node == null){ 
  56.             return;
  57.         }
  58.         inOrder(node.left,keys);
  59.         keys.add(node.key);
  60.         inOrder(node.right,keys);
  61.     }
  63.     //判断该二叉树是否是平衡二叉树
  64.     public boolean isBalanced(){ 
  65.         return isBalanced();
  66.     }
  68.     //判断以Node为根的二叉树是否是平衡二叉树，递归算法
  69.     private boolean isBalanced(Node node){ 
  70.         if(node == null){ 
  71.             return true;
  72.         }
  73.         int balanceFactor = getBalanceFactor(node);
  74.         if(Math.abs(balanceFactor) > 1){ 
  75.             return false;
  76.         }
  77.         return isBalanced(node.left) && isBalanced(node.right);
  78.     }
  80.     //获得节点的高度
  81.     private int getHeight(Node node){ 
  82.         if(node==null){ 
  83.             return 0;
  84.         }
  85.         return node.height;
  86.     }
  88.     //获得节点node的平衡因子
  89.     private int getBalanceFactor(Node node){ 
  90.         if(node == null){ 
  91.             return 0;
  92.         }
  93.         return getHeight(node.left) - getHeight(node.right);
  94.     }
  96.     //插入的元素在不平衡的节点的左侧的左侧
  97.     //对节点y进行向右旋转操作，返回旋转后新的根节点x
  98.     // y x
  99.     // / \ / \
  100.     // x T4 向右旋转（y） z y
  101.     // / \ ---------------> /\ /\
  102.     // z T3 T1 T2 T3 T4
  103.     // / \
  104.     // T1 T2
  105.     private Node rightRotate(Node y){ 
  106.         Node x = y.left;
  107.         Node T3 = x.right;
  109.         //向右旋转过程
  110.         x.right = y;
  111.         y.left = T3;
  113.         //跟新height
  114.         y.height = Math.max(getHeight(y.left),getHeight(y.right)) + 1;
  115.         x.height = Math.max(getHeight(x.left),getHeight(x.right)) + 1;
  117.         return x;
  118.     }
  120.     //插入的元素在不平衡的节点的右侧的右侧
  121.     //对节点y进行向左旋转操作，返回旋转后新的根节点x
  122.     // y x
  123.     // / \ / \
  124.     // T1 x 向左旋转（y） y z
  125.     // / \ --------------> / \ / \
  126.     // T2 z T1 T2 T3 T4
  127.     // / \
  128.     // T3 T4
  129.     private Node leftRotate(Node y){ 
  130.         Node x = y.right;
  131.         Node T2 = x.left;
  133.         //向左旋转过程
  134.         x.left = y;
  135.         y.right = T2;
  137.         //跟新height
  138.         y.height = Math.max(getHeight(y.left),getHeight(y.right)) + 1;
  139.         x.height = Math.max(getHeight(x.left),getHeight(x.right)) + 1;
  141.         return x;
  142.     }
  144.     //向二分搜索树中添加新的元素（key ，value）
  145.     @Override
  146.     public void add(K key,V value){ 
  147.         root = add(root,key,value);
  148.     }
  150.     //向node为根的二分搜索树中插入元素（key，value）,递归算法
  151.     //返回插入新节点后二分搜索树的根
  152.     private Node add(Node node,K key,V value){ 
  153.         if(node == null){ 
  154.             size++;
  155.             return new Node(key,value);
  156.         }
  157.         if(key.compareTo(node.key)<0){ 
  158.             node.left = add(node.left,key,value);
  159.         }else if(key.compareTo(node.key)>0){ 
  160.             node.right = add(node.right,key,value);
  161.         }else {  //key.compareTo(node.key}==0
  162.             node.value=value;
  163.         }
  164.         //更新height
  165.         node.height = 1 + Math.max(getHeight(node.left),getHeight(node.right));
  167.         //计算平衡因子
  168.         int balanceFactor = getBalanceFactor(node);
  169.         if(Math.abs(balanceFactor) > 1){ 
  170.             System.out.println("unbalanced :" + balanceFactor);
  171.         }
  172.         //平衡维护
  173.         //LL
  174.         if(balanceFactor > 1 && getBalanceFactor(node.left) >= 0){ 
  175.             return rightRotate(node);
  176.         }
  178.         //RR
  179.         if(balanceFactor < -1 && getBalanceFactor(node.right) <= 0){ 
  180.             return leftRotate(node);
  181.         }
  183.         //LR
  184.         if(balanceFactor > 1 && getBalanceFactor(node.left) < 0){ 
  185.             node.left = leftRotate(node.left);
  186.             return rightRotate(node);
  187.         }
  189.         //RL
  190.         if(balanceFactor < -1 && getBalanceFactor(node.right) > 0){ 
  191.             node.right = rightRotate(node.right);
  192.             return leftRotate(node);
  193.         }
  195.         return node;
  196.     }
  198.     //返回以node为节点的二分搜索树中，key所在的节点
  199.     private Node getNode(Node node,K key){ 
  200.         if(node==null){ 
  201.             return null;
  202.         }
  203.         if(key.compareTo(node.key)==0){ 
  204.             return node;
  205.         }else if(key.compareTo(node.key)<0){ 
  206.             return getNode(node.left,key);
  207.         }else
  208.             return getNode(node.right,key);
  209.     }
  211.     @Override
  212.     public boolean contains(K key){ 
  213.         return getNode(root,key) != null;
  214.     }
  216.     @Override
  217.     public V get(K key){ 
  218.         Node node=getNode(root,key);
  219.         return node == null? null : node.value;
  220.     }
  222.     @Override
  223.     public void set(K key,V newValue){ 
  224.         Node node = getNode(root,key);
  225.         if(node == null){ 
  226.             throw new IllegalArgumentException(key + "doesn't exist");
  227.         }
  228.         node.value = newValue;
  229.     }
  231.     //返回以node为根的二分搜索树的最小值所在的节点
  232.     private Node minimum(Node node){ 
  233.         if(node.left==null){ 
  234.             return node;
  235.         }
  236.         return minimum(node.left);
  237.     }
  239.     //从二分搜索树中删除键为key的节点
  240.     @Override
  241.     public V remove(K key){ 
  242.         Node node = getNode(root,key);
  243.         if(node != null){ 
  244.             root = remove(root,key);
  245.             return node.value;
  246.         }
  247.         return null;
  248.     }
  250.     //删除掉以node为根的二分搜索树中键为key的节点，递归算法
  251.     //返回删除节点后新的二分搜索树的根
  252.     private Node remove(Node node,K key){ 
  253.         if(node==null){ 
  254.             return null;
  255.         }
  257.         Node retNode;
  259.         if(key.compareTo(node.key)<0){ 
  260.             node.left = remove(node.left,key);
  261.             retNode = node;
  262.         }else if(key.compareTo(node.key)>0){ 
  263.             node.right = remove(node.right,key);
  264.             retNode = node;
  265.         }else {  //key.compareTo(node.key)==0
  266.             //删除节点左子树为空的情况
  267.             if (node.left == null) { 
  268.                 Node rightNode = node.right;
  269.                 node.right = null;
  270.                 size--;
  271.                 retNode = rightNode;
  272.             }
  273.             //删除节点右子树为空的情况
  274.             else if (node.right == null) { 
  275.                 Node leftNode = node.left;
  276.                 node.left = null;
  277.                 size--;
  278.                 retNode = leftNode;
  279.             } else { //待删除节点左右子树均不为空的情况
  280.                     //找到比待删除节点大的最小节点，即待删除节点右子树的最小节点
  281.                     //用这个节点顶替待删除节点的位置
  282.                     Node successor = minimum(node.right);
  283.                     successor.right = remove(node.right, successor.key);
  284.                     successor.left = node.left;
  285.                     node.left = node.right = null;
  286.                     retNode = successor;
  287.             }
  288.         }
  290.         if(retNode==null){ 
  291.             return null;
  292.         }
  294.         //更新height
  295.         retNode.height = 1 + Math.max(getHeight(retNode.left),getHeight(retNode.right));
  297.         //计算平衡因子
  298.         int balanceFactor = getBalanceFactor(retNode);
  300.         //平衡维护
  301.         //LL
  302.         if(balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0){ 
  303.             return rightRotate(retNode);
  304.         }
  306.         //RR
  307.         if(balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0){ 
  308.             return leftRotate(retNode);
  309.         }
  311.         //LR
  312.         if(balanceFactor > 1 && getBalanceFactor(retNode.left) < 0){ 
  313.             retNode.left = leftRotate(retNode.left);
  314.             return rightRotate(retNode);
  315.         }
  317.         //RL
  318.         if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0){ 
  319.             retNode.right = rightRotate(retNode.right);
  320.             return leftRotate(retNode);
  321.         }
  323.         return retNode;
  324.     }
  325. }

11.2基于AVL树的映射实现

  1. package _Map;
  3. public class AVLMap<K extends Comparable<K>,V> implements Map<K,V> { 
  5.     private AVLTree<K,V> avl;
  7.     public AVLMap(){ 
  8.         avl = new AVLTree<>();
  9.     }
  11.     @Override
  12.     public int getSize(){ 
  13.         return avl.getSize();
  14.     }
  16.     @Override
  17.     public boolean isEmpty(){ 
  18.         return avl.isEmpty();
  19.     }
  21.     @Override
  22.     public void add(K key,V value){ 
  23.         avl.add(key,value);
  24.     }
  26.     @Override
  27.     public boolean contains(K key){ 
  28.         return avl.contains(key);
  29.     }
  31.     @Override
  32.     public V get(K key){ 
  33.         return avl.get(key);
  34.     }
  36.     @Override
  37.     public void set(K key,V newValue){ 
  38.         avl.set(key,newValue);
  39.     }
  41.     @Override
  42.     public V remove(K key){ 
  43.         return avl.remove(key);
  44.     }
  45. }

11.3基于AVL树的集合实现

  1. package _Set;
  3. public class AVLSet<E extends Comparable<E>> implements Set<E> { 
  5.     private AVLTree<E ,Object> avl;
  7.     public AVLSet(){ 
  8.         avl = new AVLTree<>();
  9.     }
  11.     @Override
  12.     public int getSize(){ 
  13.         return avl.getSize();
  14.     }
  16.     @Override
  17.     public boolean isEmpty(){ 
  18.         return avl.isEmpty();
  19.     }
  21.     @Override
  22.     public void add(E e){ 
  23.         avl.add(e,null);
  24.     }
  26.     @Override
  27.     public boolean contains(E e){ 
  28.         return avl.contains(e);
  29.     }
  31.     @Override
  32.     public void remove(E e){ 
  33.         avl.remove(e);
  34.     }
  35. }

十二、红黑树

12.1关于红黑树

1.红黑树也是二分搜索树
2.每个节点或者是红色的，或者是黑色的
3.根节点是黑色的
4.每个叶子节点（最后的空节点）是黑色的
5.如果一个节点是红色的，那么他的孩子节点都是黑色的
6.从任意一个节点到叶子节点，经过的黑色节点是一样的
7.所有的红色节点都是左倾斜的

12.2 2-3树

1.2-3树满足二分搜索树的基本性质，但是它不是二叉树
2.节点可以存放一个元素或者两个元素
3.每个节点有2个孩子或者3个孩子
4.2-3树是一棵绝对平衡的树
5.2-3树在添加节点时，如果那一个元素为根节点的话会发生节点的融合现象
在这里插入图片描述
在这里插入图片描述
该图所对应的红黑树为：
在这里插入图片描述

12.3 2-3树添加元素的过程

添加的宗旨就是不直接添加到根节点为空的情况，若为空，需要进行融合，融合后为保持树的平衡，需要进行分裂
在这里插入图片描述在这里插入图片描述在这里插入图片描述
在这里插入图片描述在这里插入图片描述

12.4红黑树的实现

  1. **package RedBlackTree;
  3. import _Map.BSTMap;
  5. public class RBTree<K extends Comparable<K> ,V> { 
  7.     private static final boolean RED = true;
  8.     private static final boolean BLACK = false;
  10.     private class Node{ 
  11.         public K key;
  12.         public V value;
  13.         public Node left,right;
  14.         public boolean color;
  16.         public Node(K key,V value){ 
  17.             this.key = key;
  18.             this.value = value;
  19.             left = null;
  20.             right = null;
  21.         }
  22.     }
  24.     private Node root;
  25.     private int size;
  27.     public RBTree(){ 
  28.         root = null;
  29.         size = 0;
  30.     }
  32.     public int getSize(){ 
  33.         return size;
  34.     }
  36.     public boolean isEmpty(){ 
  37.         return size == 0;
  38.     }
  40.     //判断节点node的颜色
  41.     private boolean isRed(Node node){ 
  42.         if(node == null){ 
  43.             return BLACK;
  44.         }
  45.         return node.color;
  46.     }
  48.     // node x
  49.     // / \ 左旋转 / \
  50.     // T1 x ---------> node T3
  51.     // / \ / \
  52.     // T2 T3 T1 T2
  53.     private Node leftRotate(Node node){ 
  54.         Node x = node.right;
  56.         //左旋转
  57.         node.right = x.left;
  58.         x.left = node;
  60.         x.color = node.color;
  61.         node.color = RED;
  62.         return x;
  63.     }
  65.     // node x
  66.     // / \ 右旋转 / \
  67.     // x T2 --------> y node
  68.     // / \ / \
  69.     // y T1 T1 T2
  70.     private Node rightRotate(Node node){ 
  71.         Node x = node.left;
  73.         //右旋转
  74.         node.left = x.right;
  75.         x.right = node;
  77.         x.color = node.color;
  78.         node.color = RED;
  80.         return x;
  81.     }
  83.     //颜色翻转
  84.     private void flipColors(Node node){ 
  85.         node.color = RED;
  86.         node.left.color = BLACK;
  87.         node.right.color = BLACK;
  88.     }
  90.     //向红黑树中添加新的元素（key，value）
  91.     public void add(K key, V value){ 
  92.         root = add(root,key,value);
  93.         root.color = BLACK; //最终根节点为黑色节点
  94.     }
  96.     //向以node为根的红黑树中插入元素（key, value），递归算法
  97.     //返回插入新节点后红黑树的根
  98.     private Node add(Node node,K key,V value){ 
  99.         if(node == null){ 
  100.             size++;
  101.             return new Node(key,value); //默认插入红色节点
  102.         }
  103.         if(key.compareTo(node.key) < 0){ 
  104.             node.left = add(node.left,key,value);
  105.         }else if(key.compareTo(node.key) > 0){ 
  106.             node.right = add(node.right,key,value);
  107.         }else{   //key.compareTo(node.key) == 0
  108.             node.value = value;
  109.         }
  111.         if(isRed(node.right) && !isRed(node.left)){ 
  112.             node = leftRotate(node);
  113.         }
  115.         if(isRed(node.left) && isRed(node.left.left)){ 
  116.             node = rightRotate(node);
  117.         }
  119.         if(isRed(node.left) && isRed(node.right)){ 
  120.             flipColors(node);
  121.         }
  122.         return node;
  123.     }
  125.     //返回以node为节点的二分搜索树中，key所在的节点
  126.     private Node getNode(Node node, K key){ 
  127.         if(node==null){ 
  128.             return null;
  129.         }
  130.         if(key.equals(node.key)){ 
  131.             return node;
  132.         }else if(key.compareTo(node.key)<0){ 
  133.             return getNode(node.left,key);
  134.         }else{   //if(key.compareTo(node.key) > 0)
  135.             return getNode(node.right,key);
  136.         }
  137.     }
  139.     public boolean contains(K key){ 
  140.         return getNode(root,key) != null;
  141.     }
  143.     public V get(K key){ 
  144.         Node node=getNode(root,key);
  145.         return node == null? null : node.value;
  146.     }
  148.     public void set(K key,V newValue){ 
  149.         Node node = getNode(root,key);
  150.         if(node == null){ 
  151.             throw new IllegalArgumentException(key + "doesn't exist");
  152.         }
  153.         node.value = newValue;
  154.     }
  156.     //返回以node为根的二分搜索树的最小值所在的节点
  157.     private Node minimum(Node node){ 
  158.         if(node.left==null){ 
  159.             return node;
  160.         }
  161.         return minimum(node.left);
  162.     }
  164.     //删除掉以node为根的二分搜索树中的最小节点
  165.     //返回删除节点后新的二分搜索树的根
  166.     private Node removeMin(Node node){ 
  167.         if(node.left == null){ 
  168.             Node rightNode = node.right;
  169.             node.right=null;
  170.             size--;
  171.             return rightNode;
  172.         }
  173.         node.left = removeMin(node.left);
  174.         return node;
  175.     }
  177.     //从二分搜索树中删除键为key的节点
  178.     public V remove(K key){ 
  179.         Node node = getNode(root,key);
  180.         if(node != null){ 
  181.             root = remove(root,key);
  182.             return node.value;
  183.         }
  184.         return null;
  185.     }
  187.     //删除掉以node为根的二分搜索树中键为key的节点，递归算法
  188.     //返回删除节点后新的二分搜索树的根
  189.     private Node remove(Node node, K key){ 
  190.             if(node==null){ 
  191.             return null;
  192.         }
  193.         if(key.compareTo(node.key)<0){ 
  194.             node.left = remove(node.left,key);
  195.             return node;
  196.         }else if(key.compareTo(node.key)>0){ 
  197.             node.right = remove(node.right,key);
  198.             return node;
  199.         }else{  //key.compareTo(node.key)==0
  200.             //删除节点左子树为空的情况
  201.             if(node.left == null){ 
  202.                 Node rightNode = node.right;
  203.                 node.right = null;
  204.                 size--;
  205.                 return rightNode;
  206.             }
  207.             //删除节点右子树为空的情况
  208.             if(node.right == null){ 
  209.                 Node leftNode = node.left;
  210.                 node.left = null;
  211.                 size--;
  212.                 return leftNode;
  213.             }
  214.             //待删除节点左右子树均不为空的情况
  215.             //找到比待删除节点大的最小节点，即待删除节点右子树的最小节点
  216.             //用这个节点顶替待删除节点的位置
  217.             Node successor = minimum(node.right);
  218.             successor.right = removeMin(node.right);
  219.             successor.left = node.left;
  220.             node.left = node.right = null;
  221.             return successor;
  222.         }
  223.     }
  224. }
  225. **

12.5红黑树的性能总结

1.对于完全随机的数据，普通的二分搜索树很好用
2.缺点：极端退化成链表（或者高度不平衡）
3.对于查询较多的情况，使用AVL树
4.统计性能更优（增删改查等操作）

十三、哈希表

什么是哈希表？
每个字符都有一个索引相对应。

实现哈希表（增删改查等方法）

  1. package _HashTable;
  2. import java.util.TreeMap;
  3. public class HashTable<K,V> { 
  4.     private final int[] capacity = { 53,97,193,389,749,1543,3079,6151,
  5.     12289,24593,19157,98317,196613,393241,786433,1572869,3145739,6291469,
  6.     12582917,25165843,50331653,100263319,20132611,402653189,805306457,1610612741};
  8.     private static final int upperTol = 10;
  9.     private static final int lowerTol = 2;
  10.     private static  int capacityIndex=0;
  11.     private TreeMap<K,V>[] hashtable;
  12.     private int M;
  13.     private int size;
  15.     public HashTable(int M){ 
  16.         this.M =capacity[capacityIndex];
  17.         size = 0;
  18.         hashtable = new TreeMap[M];
  20.         for(int i=0;i<M;i++){ 
  21.             hashtable[i] = new TreeMap<>();
  22.         }
  23.     }
  25.     private int hash(K key){ 
  26.         return (key.hashCode() & 0x7fffffff) % M;
  27.     }
  29.     public int getSize(){ 
  30.         return size;
  31.     }
  33.     public void add(K key,V value){ 
  34.         TreeMap<K,V> map = hashtable[hash(key)];
  35.         if(map.containsKey(key)){ 
  36.             map.put(key,value);
  37.         }else{ 
  38.             map.put(key,value);
  39.             size++;
  41.             if(size >= upperTol * M && capacityIndex+1 < capacity.length){ 
  42.                 capacityIndex++;
  43.                 resize(capacity[capacityIndex]);
  44.             }
  45.         }
  46.     }
  48.     public V remove(K key){ 
  49.         TreeMap<K,V> map = hashtable[hash(key)];
  50.         V ret = null;
  51.         if(map.containsKey(key)){ 
  52.             ret = map.remove(key);
  53.             size--;
  55.             if(size < lowerTol * M && capacityIndex-1 >=0){ 
  56.                 capacityIndex--;
  57.                 resize(capacity[capacityIndex]);
  58.             }
  59.         }
  60.         return ret;
  61.     }
  63.     public void set(K key,V value){ 
  64.         TreeMap<K,V> map = hashtable[hash(key)];
  65.         if(!map.containsKey(key)){ 
  66.             throw new IllegalArgumentException(key + "doesn't exist");
  67.         }
  68.         map.put(key,value);
  69.     }
  71.     public boolean contains(K key){ 
  72.         return hashtable[hash(key)].containsKey(key);
  73.     }
  75.     public V get(K key){ 
  76.         return hashtable[hash(key)].get(key);
  77.     }
  79.     private void resize(int newM){ 
  80.         TreeMap<K,V>[] newHashTable = new TreeMap[newM];
  81.         for(int i=0;i<newM;i++){ 
  82.             newHashTable[i] = new TreeMap<>();
  83.         }
  85.         int oldM=M;
  86.         this.M = newM;
  87.         for(int i=0;i<oldM;i++){ 
  88.             TreeMap<K,V> map = hashtable[i];
  89.             for(K key:map.keySet()){ 
  90.                 newHashTable[hash(key)].put(key,map.get(key));
  91.             }
  92.         }
  93.         this.hashtable=newHashTable;
  94.     }
  95. }

发表评论

表情：
评论列表 （有 0 条评论，53人围观）

还没有评论，来说两句吧...

相关阅读