算法导论学习笔记第七章快速排序-蒲公英云

算法导论学习笔记第七章快速排序

青旅半醒 2023-01-14 01:45 243阅读 0赞

快排最坏时间复杂度为θ（n²），但它的平均性能很好，通常是实际排序应用中最好的选择，它的期望时间复杂度为θ（nlgn），且θ（nlgn）中隐含的常数因子非常小，且它还能进行原址排序。

快排也使用了分治思想：
1.分解：数组被划分为两个子数组，使得一个子数组中的每个元素都小于A[q]，而另一个子数组中的每个元素都大于A[q]。
2.解决：通过递归调用快排，对两个子数组进行排序。
3.合并：子数组都是原址排序，不需要合并操作。

快排伪代码：

QUICKSORT(A, p, r):
if p < r
    q = PARTITIO
|  |  |
|--|--|
|  |  |
N(A, p, r)
    QUICKSORT(A, p, q - 1)
    QUICKSORT(A, q + 1, r)

PARTITION过程：

PARTITION(A, p, r):
x = A[r]
i = p - 1
for j = p to r - 1
    if A[j] <= x
        i = i + 1
        exchange A[i] with A[j]
exchange A[i + 1] with A[r]
return i + 1

以下是PARTITION图解，它选择x=A[r]作为主元，并围绕它来划分子数组：
在这里插入图片描述
PARTITION的时间复杂度为O（n）。

当数组中的值都相同时，PARTITION返回r，可以使算法在数组中所有值都相同时，返回一个中间的值。

快排的运行时间依赖于划分是否平衡，而平衡与否依赖于用于划分的元素。

当划分产生的两个子问题分别包含n-1个元素和0个元素时，快排的最坏情况发生，此时时间复杂度为θ（n²）。

快排的最好情况是每一层递归都平衡划分子数组，即PARTITION得到的两个子问题的规模都不大于n/2（一个⌊n/2⌋，一个⌈n/2⌉-1），此时时间复杂度为θ（nlgn）。

快排的平均运行时间更接近其最好情况，即使每次划分子数组总是产生9:1的划分：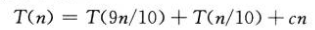
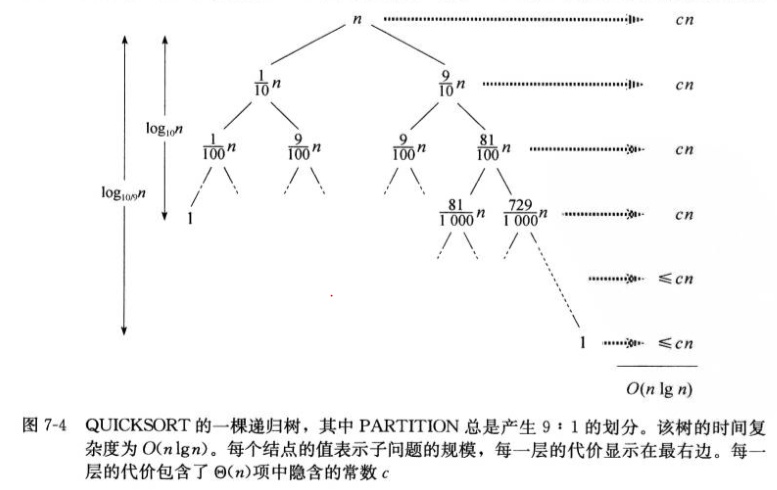
在这里插入图片描述

虽然递归每一层都产生9:1的划分，直观上看起来非常不平衡，但运行时间还是O（nlgn）。事实上，任何一种常数比例的划分都会产生θ（lgn）的递归树，其中每一层的代价都是O（n）。

一个好的和坏的划分交替出现的序列和每次都是完美划分的序列快排时的时间复杂度相同，只是前者情况下，O符号中隐含的常数因子大一些：
在这里插入图片描述
对几乎有序的序列排序时，插入排序性能往往要由于快排。

我们可以通过在算法中引入随机性，使得算法对于所有输入都能获得较好的期望性能。我们可以采用随机抽样的方法选出主元：

RANDOMIZED-PARTITION(A, p, r):
i = RANDOM(p, r)
exchange A[r] with A[i]
return PARTITION(A, p, r)

使用随机方法选主元的快排代码：

#include <iostream>
#include <vector>
#include <random>
#include <time.h>
using namespace std;
size_t partition(vector<int> &ivec, size_t start, size_t end) { 
    uniform_int_distribution<size_t> u(start, end);
    default_random_engine e(time(0));
    size_t rand = u(e);
    swap(ivec[end], ivec[rand]);
    size_t firstBigIndex = start;
    for (size_t i = start; i < end; ++i) { 
        if (ivec[i] < ivec[end]) { 
            swap(ivec[i], ivec[firstBigIndex]);
            ++firstBigIndex;
        }
    }
    swap(ivec[firstBigIndex], ivec[end]);
    return firstBigIndex;
}
void quickSort(vector<int> &ivec, size_t start, size_t end) { 
    size_t mid = partition(ivec, start, end);
    if (start < mid) { 
        quickSort(ivec, start, mid - 1);
    }
    if (end > mid) { 
        quickSort(ivec, mid + 1, end);
    }
}
int main() { 
    vector<int> ivec = {  4,5,7,3,2,1,9,6 };
    quickSort(ivec, 0, ivec.size() - 1);
    for (int i : ivec) { 
        cout << i;
    }
    cout << endl;
}

当输入数据几乎有序时，插入排序速度很快，可以利用它提高快排的速度，当对一个长度小于k的子数组调用快排时，让它不做任何排序就返回，当上层快排调用返回后，对整个数组运行插入排序完成排序过程，这一算法的时间复杂度为O（nk+nlg（n/k）），理论上，k的取值为：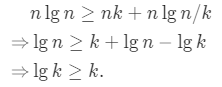
在这里插入图片描述
这是不可能的，如果加上常数因子：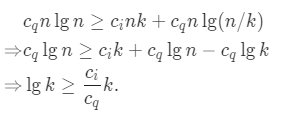

实践中，需要根据实验测试k的取值。

可对PARTITION过程选主元的过程改为从数组总随机选3个元素，选择中间大小的数字作为主元所在下标。

Hoare设计的划分算法：

HOARE-PARTITION(A, p, r):
x = A[p]
i = p - 1
j = r + 1
while TRUE
    repeat 
        j = j - 1
    until A[j] <= x
    repeat 
        i = i + 1
    until A[j] >= x
    if i < j
        exchange A[i] with A[j]
    else 
        return j

由于以上代码运行时永远都有p≤i<j≤r ，因此不会访问到A之外的内存。

使用以上过程的快排代码：

#include <iostream>
#include <vector>
using namespace std;
int partition(vector<int> &ivec, int start, int end) { 
    int sign = ivec[start];
    int l = start - 1;
    int r = end + 1;
    while (true) { 
        do { 
            --r;
        } while (ivec[r] > sign);
        do { 
            ++l;
        } while (ivec[l] < sign);
        if (l < r) { 
            swap(ivec[l], ivec[r]);
        } else {     // 返回前，整个数组分为两部分，start~j子数组中的元素小于等于从j+1~end子数组中的元素
            return r;
        }
    }
}
void quickSort(vector<int> &ivec, int start, int end) { 
    if (start >= end) { 
        return;
    }
    int mid = partition(ivec, start, end);
    quickSort(ivec, start, mid);
    quickSort(ivec, mid + 1, end);
}
int main() { 
    vector<int> ivec = {  8,6,9,5,3,2,0,1,4,7,6,9,2,3 };
    quickSort(ivec, 0, ivec.size() - 1);
    for (int i : ivec) { 
        cout << i;
    }
    cout << endl;
}