论文：https://arxiv.org/abs/1608.03665
代码：https://github.com/wenwei202/caffe/tree/scnn

1 核心思想

前面两篇文章https://blog.csdn.net/cdknight_happy/article/details/110953977和https://blog.csdn.net/cdknight_happy/article/details/111051396介绍的都是非结构化的剪枝，只是从每一层中移除了一些不重要的连接，但是本文作者的实验发现在CPU/GPU上，这种非常规的存储访问方式的实际加速效果非常有限。如下图所示，是对于AlexNet应用L1非结构化剪枝前后的速度对比，剪枝后模型准确率的衰减不超过2%：
在这里插入图片描述上图可以表明，即便模型剪枝后稀疏度很大(例如，超过了95%)，但由于权重的分布非常广泛，局部相关性很小，得到的实际加速效果也非常有限。

使用低秩近似进行模型压缩时，一般都是先完成模型的训练，然后模型中的权重矩阵会用多个低秩矩阵的乘积近似，最后再进行模型的微调以提升准确率。低秩近似因为进行了矩阵的分解，可以取得有效的加速。但是，低秩近似只能应用于单个网络层，无法修改网络的结构。

本文作者受三个事实的启发：

模型中包含了冗余的滤波器和连接；
CNN中一般使用的是三维卷积，但其实可以使用任意形状的卷积以消除不必要的计算；
因为梯度爆炸和梯度弥散问题，并不是网络越深效果越好。

提出了结构化稀疏学习(structured sparisity learning,SSL)，通过Group Lasso进行模型的结构化剪枝。

1.1 SSL总体思路

假设DNN的某层是一个四维tensor， W ( l ) ∈ R N l × C l × M l × K l W^{(l)} \in R^{N_l \times C_l \times M_l \times K_l} W(l)∈RNl×Cl×Ml×Kl，L表示模型总的层数。SSL优化总的思路可以写成：
在这里插入图片描述
E D ( W ) E_D(W) ED(W)表示数据上的损失； R ( . ) R(.) R(.)表示非结构化的正则化项； R g ( . ) R_g(.) Rg(.)表示应用于每一层的结构化稀疏项。因为Group Lasso可以将一组参数全部变为0，所以作者用它来实现 R g ( . ) R_g(.) Rg(.)，公式为 R g ( w ) = ∑ g = 1 G ∣ ∣ w ( g ) ∣ ∣ g R_g(w) = \sum_{g=1}^{G}||w^{(g)}||_g Rg(w)=∑g=1G∣∣w(g)∣∣g， w ( g ) w^{(g)} w(g)表示一组参数， ∣ ∣ . ∣ ∣ g ||.||_g ∣∣.∣∣g表示group lasso， ∣ ∣ w ( g ) ∣ ∣ g = ∑ i = 1 ∣ w ( g ) ∣ ( w i ( g ) ) 2 ||w^{(g)}||_g = \sqrt{\sum_{i=1}^{|w^{(g)}|}(w_i^{(g)})^2} ∣∣w(g)∣∣g=∑i=1∣w(g)∣(wi(g))2， ∣ w ( g ) ∣ |w^{(g)}| ∣w(g)∣是 w ( g ) w^{(g)} w(g)中的权重数量。

1.2 在filters、channels、filters shape和depth四个维度应用SSL

group lasso中如何分组，就决定了在哪个维度进行SSL。作者提到了四种维度：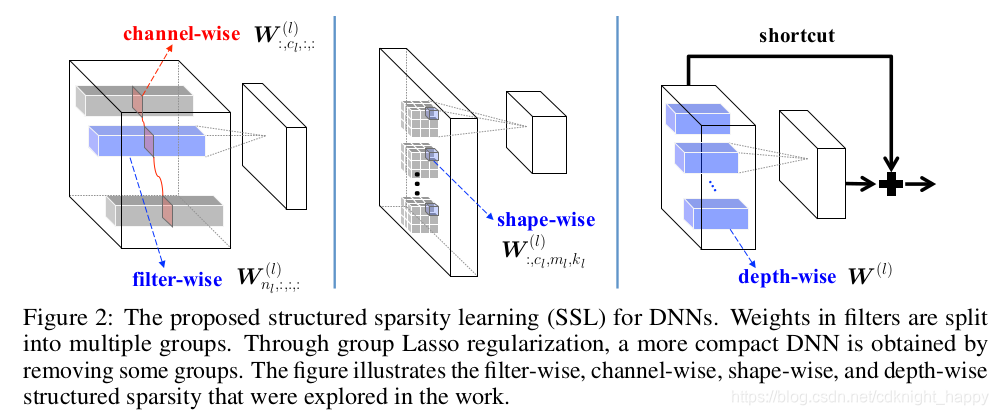
在这里插入图片描述 filter-wise去掉某个filter；channel-wise去掉所有filter的某个channel；shape-wise调整filter的形状；depth-wise整体去掉某个网络层。

下面所列的公式中全部忽略了非结构化稀疏项 R ( . ) R(.) R(.)。

1.2.1 filter & channel SSL

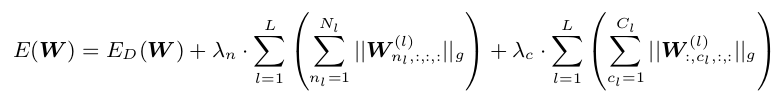
在这里插入图片描述
W n l , : , : , : ( l ) W^{(l)}_{n_l,:,:,:} Wnl,:,:,:(l)表示第 l l l层的第 n l n_l nl个滤波器； W : , c l , : , : ( l ) W_{:,c_l,:,:}^{(l)} W:,cl,:,:(l)表示第 l l l层中所有滤波器的第 c l c_l cl个channel。上面的公式中，是吧filter-wise和channel-wise SSL同步进行，这是因为如果进行了filter SSL，某个filter全部被置为0，计算之后也就生成了一个全为0的输出feature map，filter-wise SSL和channel-wise SSL是互补影响的，因此两者可以同步进行。

1.2.2 shape SSL

使用 W : , c l , m l , k l ( l ) W^{(l)}_{:,c_l,m_l,k_l} W:,cl,ml,kl(l)表示由第 c l c_l cl个channel中所有二维滤波器在 ( m l , k l ) (m_l,k_l) (ml,kl)位置组成的向量，shape SSL是指可以把某些系数裁剪掉，其计算公式为：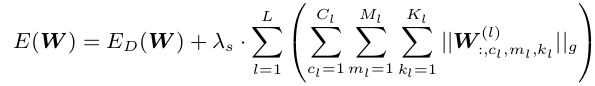
在这里插入图片描述

1.2.3 depth SSL

depth SSL是指可以把某些层裁剪掉，其计算公式为：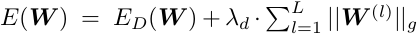
在这里插入图片描述
裁剪掉某层之后，会造成模型的信息传递被中断，所以作者使用了shortcut连接，如Fig. 2所示，如果某层被裁剪掉之后，前面层的信息会通过shortcut直接传输到后面层。

1.2.4 两种稀疏规则的实际实现

对卷积应用2D filter-wise稀疏：3D卷积是2D卷积的组合，进行1.2.1节所述的filter-wise SSL时，可以按照channel进行group lasso，也就是对 W n l , c l , : , : ( l ) W_{n_l,c_l,:,:}^{(l)} Wnl,cl,:,:(l)应用SSL。

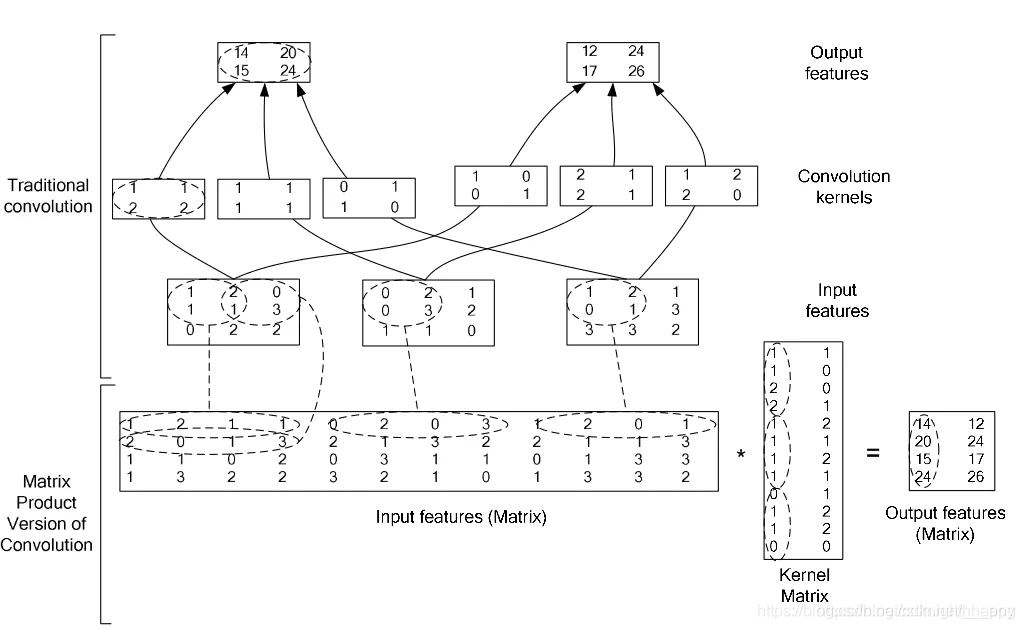
针对GEMM结合使用filter-wise和shape-wise SSL：DNN的实现中，一般都是将卷积运算转成矩阵运算，例如在caffe中，就是通过im2col进行卷积运算，在下面的列子中，将 W n l , : , : , : ( l ) W_{n_l,:,:,:}^{(l)} Wnl,:,:,:(l)转换为了权重矩阵的一列，将 W , : , c l , m l , k l ( l ) W_{,:,c_l,m_l,k_l}^{(l)} W,:,cl,ml,kl(l)转换为了权重矩阵的一行。所以对权重矩阵进行稀疏化，同时移除掉某行和某列，就相当于同时进行filter-wise和shape-wise SSL。

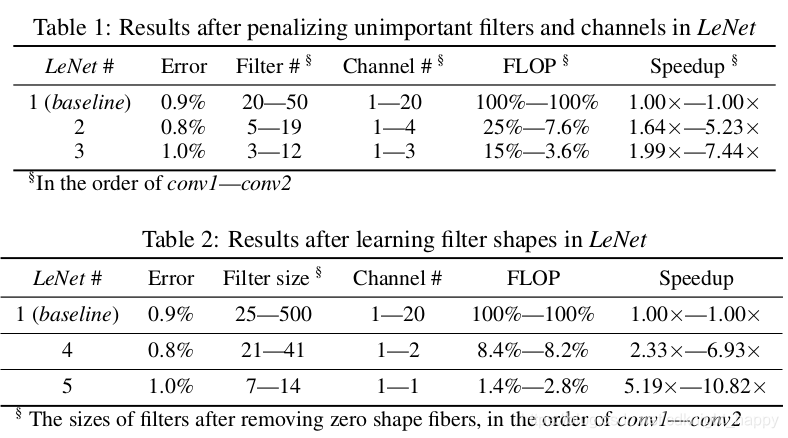
在这里插入图片描述