[Leetcode][第60题][JAVA][第k个排列][回溯][DFS][剪枝]-蒲公英云

[Leetcode][第60题][JAVA][第k个排列][回溯][DFS][剪枝]

忘是亡心i 2022-12-04 02:27 210阅读 0赞

【问题描述】[中等]

在这里插入图片描述

【解答思路】

1. 回溯搜索算法 + 剪枝，直接来到叶子结点

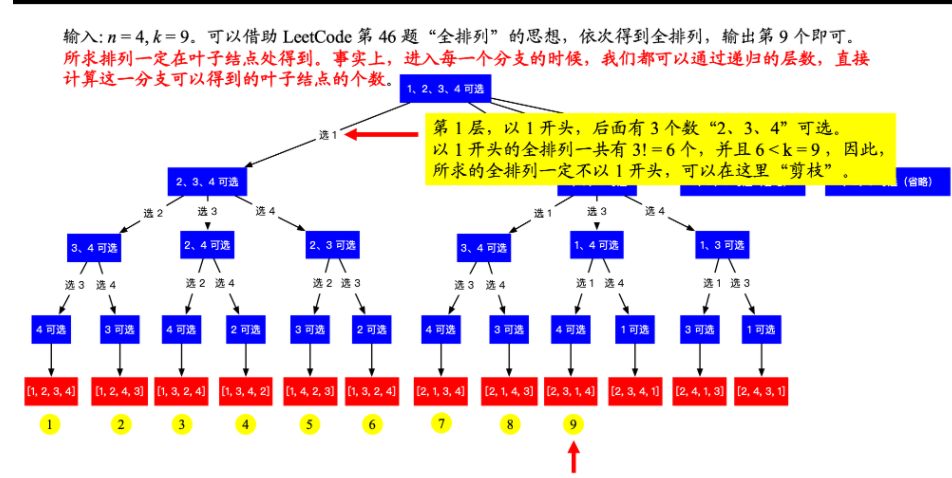
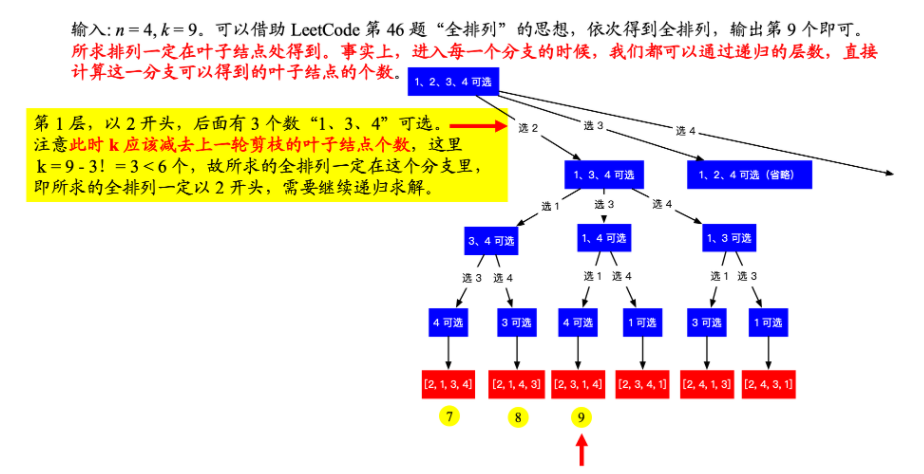
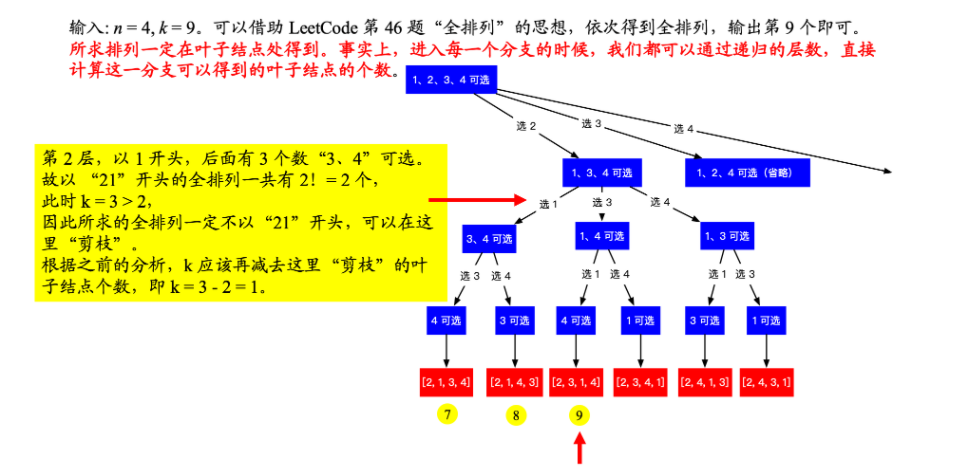
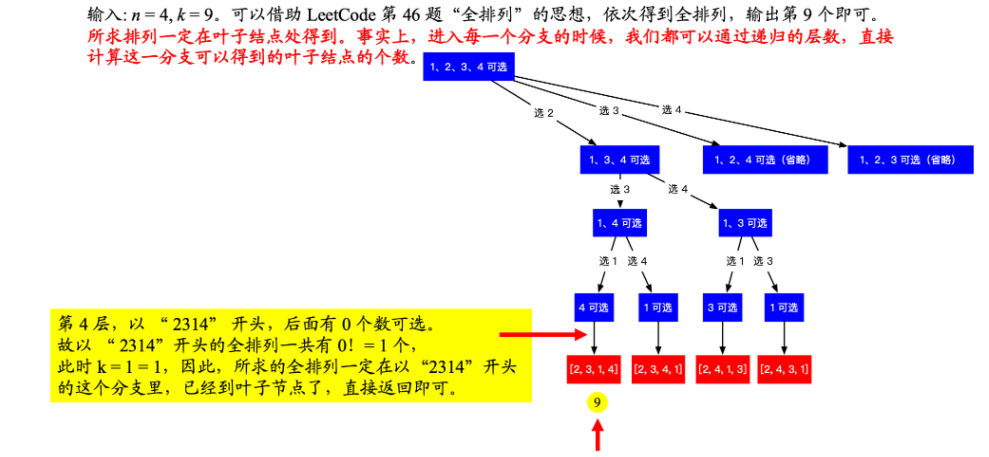
在这里插入图片描述

时间复杂度：O(N^2) 空间复杂度：O(N)
在这里插入图片描述

import java.util.Arrays;
public class Solution { 
    /** * 记录数字是否使用过 */
    private boolean[] used;
    /** * 阶乘数组 */
    private int[] factorial;
    private int n;
    private int k;
    public String getPermutation(int n, int k) { 
        this.n = n;
        this.k = k;
        calculateFactorial(n);
        // 查找全排列需要的布尔数组
        used = new boolean[n + 1];
        Arrays.fill(used, false);
        StringBuilder path = new StringBuilder();
        dfs(0, path);
        return path.toString();
    }
    /** * @param index 在这一步之前已经选择了几个数字，其值恰好等于这一步需要确定的下标位置 * @param path */
    private void dfs(int index, StringBuilder path) { 
        if (index == n) { 
            return;
        }
        // 计算还未确定的数字的全排列的个数，第 1 次进入的时候是 n - 1
        int cnt = factorial[n - 1 - index];
        for (int i = 1; i <= n; i++) { 
            if (used[i]) { 
                continue;
            }
            if (cnt < k) { 
                k -= cnt;
                continue;
            }
            path.append(i);
            used[i] = true;
            dfs(index + 1, path);
            // 注意 1：没有回溯（状态重置）的必要
            // 注意 2：这里要加 return，后面的数没有必要遍历去尝试了
            return;
        }
    }
    /** * 计算阶乘数组 * * @param n */
    private void calculateFactorial(int n) { 
        factorial = new int[n + 1];
        factorial[0] = 1;
        for (int i = 1; i <= n; i++) { 
            factorial[i] = factorial[i - 1] * i;
        }
    }
}
作者：liweiwei1419
链接：https://leetcode-cn.com/problems/permutation-sequence/solution/hui-su-jian-zhi-python-dai-ma-java-dai-ma-by-liwei/

2. 有序数组（链表）模拟

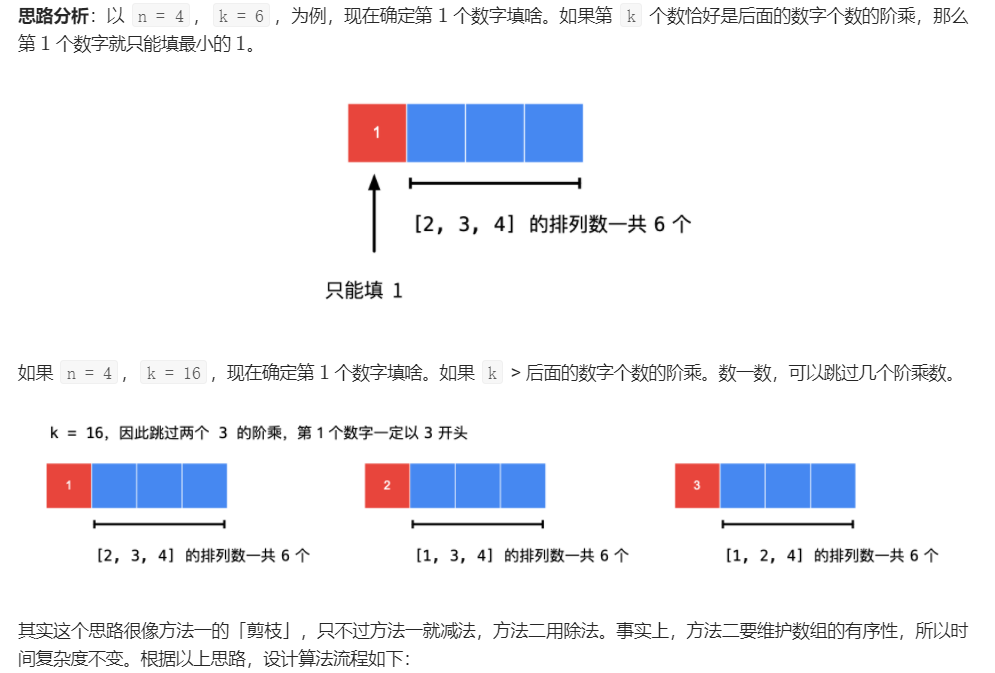
在这里插入图片描述

时间复杂度：O(N2) 空间复杂度：O(N)

import java.util.LinkedList;
import java.util.List;
public class Solution { 
    public String getPermutation(int n, int k) { 
        // 注意：相当于在 n 个数字的全排列中找到下标为 k - 1 的那个数，因此 k 先减 1
        k --;
        int[] factorial = new int[n];
        factorial[0] = 1;
        // 先算出所有的阶乘值
        for (int i = 1; i < n; i++) { 
            factorial[i] = factorial[i - 1] * i;
        }
        // 这里使用数组或者链表都行
        List<Integer> nums = new LinkedList<>();
        for (int i = 1; i <= n; i++) { 
            nums.add(i);
        }
        StringBuilder stringBuilder = new StringBuilder();
        // i 表示剩余的数字个数，初始化为 n - 1
        for (int i = n - 1; i >= 0; i--) { 
            int index = k / factorial[i] ;
            stringBuilder.append(nums.remove(index));
            k -= index * factorial[i];
        }
        return stringBuilder.toString();
    }
}
作者：liweiwei1419
链接：https://leetcode-cn.com/problems/permutation-sequence/solution/hui-su-jian-zhi-python-dai-ma-java-dai-ma-by-liwei/

【总结】

1. 剪枝大法好充分利用条件边界减少回溯

2.回溯思想

【数据结构与算法】【算法思想】回溯算法

3.常规思路超时全排列 dfs传递的是深度不是具体某一个值

相关题目
[Leedcode][JAVA][第46题][全排列][回溯算法]

class Solution { 
    private static String str = "";
    public String getPermutation(int n, int k) { 
        List<String> a =new ArrayList<String>();
        boolean[] used = new  boolean[n];
        int[]num = new int[n];
        for(int i =0 ;i<n;i++){ 
            num[i] = i+1;
        }
        permunte(0,n,num,a,used,k,"");
        return str;
    }
     private void permunte(int depth, int n,int[] num, List<String> a,boolean[] used ,int  k,String s){ 
         if(s.length() == n){ 
             a.add(s);
             if(a.size() == k){ 
                 str = s;
                return ;
            }
         }
           for(int i=0;i<n;i++){ 
                StringBuffer sb = new StringBuffer(s);
                    if(!used[i]){ 
                        used[i] = true;
                        sb.append(num[i]);
                        permunte(depth+1,n,num,a,used,k,sb.toString());
                        used[i] = false;
                        sb.deleteCharAt(sb.length()-1);
                    }
            }
     }
}