494. 目标和

不念不忘少年蓝@ 2022-12-02 01:12 112阅读 0赞

# 题目： #

[494. 目标和][494.]  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3p5eF9seQ_size_16_color_FFFFFF_t_70_pic_center]

# 题解： #

## 1. 题解一：DFS枚举 ##

![在这里插入图片描述][20200828232753982.png_pic_center]

## 2. 题解二：动态规划（首选） ##

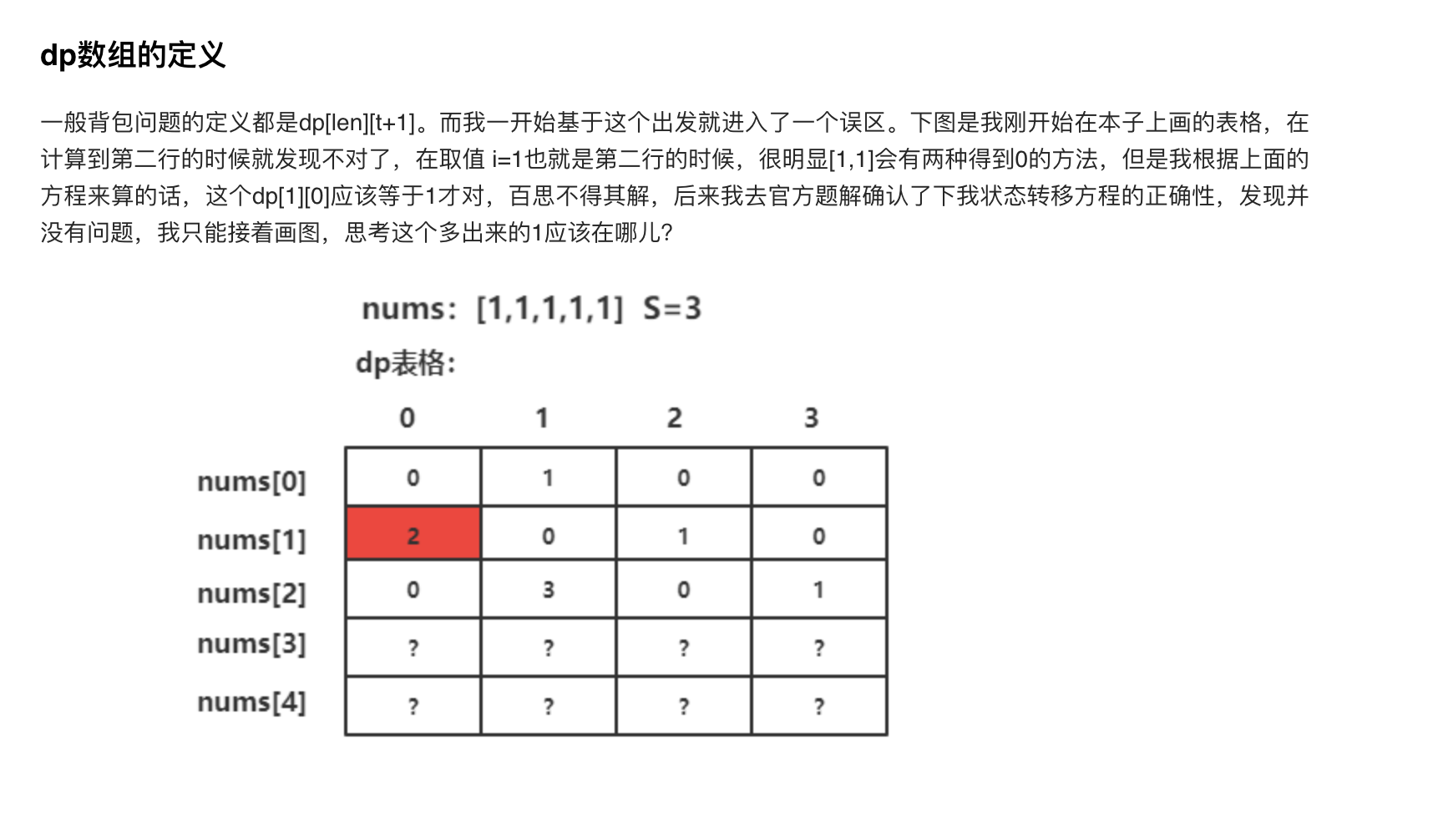
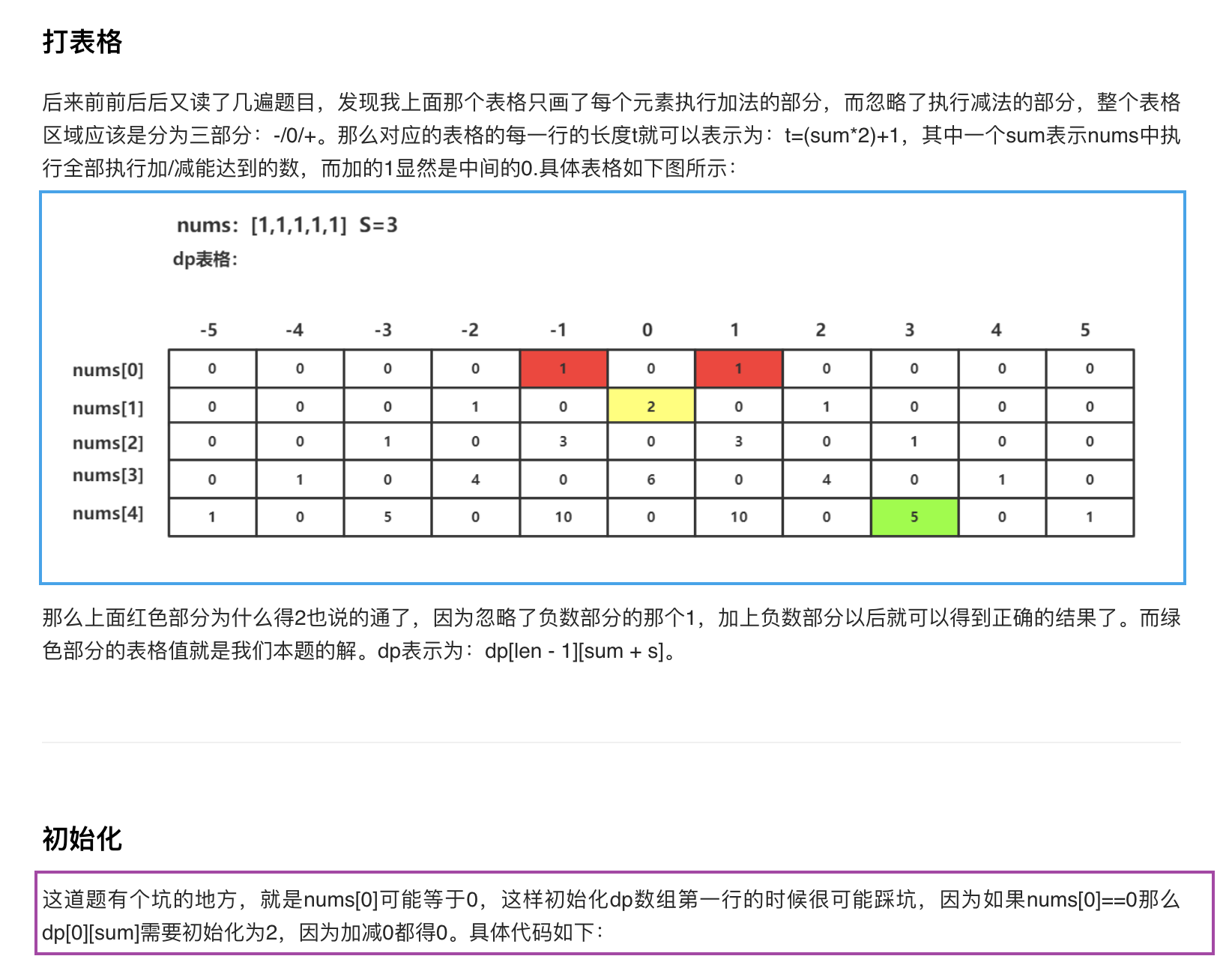
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3p5eF9seQ_size_16_color_FFFFFF_t_70_pic_center 1]  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3p5eF9seQ_size_16_color_FFFFFF_t_70_pic_center 2]  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3p5eF9seQ_size_16_color_FFFFFF_t_70_pic_center 3]

# 代码： #

## 1. 代码一：DFS枚举 ##

public class code494 { 
    
        // 方法一: DFS枚举
        public int count = 0;
    
        public int findTargetSumWays(int[] nums, int S)
        { 
            dfs(nums, S, 0, 0);
            return count;
        }
    
        public void dfs(int nums[], int S, int i, int sum)
        { 
            if(i == nums.length && sum == S)
            { 
                count++;
                return;
            }
            if(i == nums.length)
            { 
                return;
            }
            dfs(nums, S, i + 1, sum + nums[i]);
            dfs(nums, S, i + 1, sum - nums[i]);
        }
        
        public static void main(String[] args) { 
            int nums[] = {  1, 1, 1, 1, 1 };
            int S = 3;
    
            code494 test = new code494();
            int res = test.findTargetSumWays(nums, S);
            System.out.println(res);
        }
    }

## 2. 代码二：动态规划（首选） ##

public class code494 { 
    
        // 方法二: 动态规划
        public int findTargetSumWays(int[] nums, int S) { 
            int sum = 0;
            for(int i = 0; i < nums.length; i++)
            { 
                sum = sum + nums[i];
            }
            // 绝对值范围超过了sum的绝对值范围则无法得到
            if(Math.abs(S) > Math.abs(sum))
            { 
                return 0;
            }
            int len = nums.length;
            // - 0 +
            int target = sum * 2 + 1;
            // dp[i][j]: 从数组 nums 中 0 —— i 的元素(前 i 个元素)进行加减，可以得到 j 的方法数量。
            int dp[][] = new int[len][target];
    
            // 初始化
            if(nums[0] == 0)
            { 
                dp[0][sum] = 2; // 如果 nums[0] == 0 那么 dp[0][sum] 需要初始化为2，因为加减 0 都得0。
            }
            // 初始化表格的第一行，sum表示的是表格中【0】所在的那一列的下标；
            // 而对 nums[0] 执行加减呢，是因为当前 nums[0] 这个数可以执行一次加，也可以执行一次减；
            // 而为什么赋值为 1 呢，是因为当前这个 nums[0] 能够得到对应的值的情况只有一种。
            else
            { 
                dp[0][sum + nums[0]] = 1;
                dp[0][sum - nums[0]] = 1;
            }
            for(int i = 1; i < len; i++)
            { 
                for(int j = 0; j < target; j++)
                { 
                    // 边界处理
                    int left = (j - nums[i]) >= 0 ? j - nums[i]: 0;
                    int right = (j + nums[i]) < target ? j + nums[i]: 0;
                    // nums[i] 这个元素我可以执行加，还可以执行减，那么 dp[i][j] 的结果值就是加/减之后对应位置的和。
                    dp[i][j] = dp[i - 1][left] + dp[i - 1][right];
                }
            }
            return dp[len - 1][sum + S];
        }
        
        public static void main(String[] args) { 
            int nums[] = {  1, 1, 1, 1, 1 };
            int S = 3;
    
            code494 test = new code494();
            int res = test.findTargetSumWays(nums, S);
            System.out.println(res);
        }
    }

# 参考： #

1.  [目标和][Link 1]
2.  [换一下角度，可以转换为典型的01背包问题][01]
3.  [动态规划思考全过程][Link 2]
4.  [C++ dfs和01背包][C_ dfs_01]
5.  [背包打卡题2：0-1背包恰好装满背包的方案数][2_0-1]
6.  [494. 目标和][494. 1]
7.  [Python3 DFS 与 01背包 与 动态规划 三种方法详解][Python3 DFS _ 01_ _ _]
8.  [动态规划击败了98%的java用户][98_java]

[494.]: https://leetcode-cn.com/problems/target-sum/
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3p5eF9seQ_size_16_color_FFFFFF_t_70_pic_center]: /images/20221123/e41388bdb6a5450090885fe0dbb02e7c.png
[20200828232753982.png_pic_center]: /images/20221123/0dc3788b858e4e88b12da543d1540804.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3p5eF9seQ_size_16_color_FFFFFF_t_70_pic_center 1]: /images/20221123/38c52de40a4047d997ac1ad4b63f8ae4.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3p5eF9seQ_size_16_color_FFFFFF_t_70_pic_center 2]: /images/20221123/1cf06f91c0e44c679ab12fd7b20543b2.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3p5eF9seQ_size_16_color_FFFFFF_t_70_pic_center 3]: /images/20221123/1612fd4b4b224eef9830f67d9398b2c6.png
[Link 1]: https://leetcode-cn.com/problems/target-sum/solution/mu-biao-he-by-leetcode/
[01]: https://leetcode-cn.com/problems/target-sum/solution/huan-yi-xia-jiao-du-ke-yi-zhuan-huan-wei-dian-xing/
[Link 2]: https://leetcode-cn.com/problems/target-sum/solution/dong-tai-gui-hua-si-kao-quan-guo-cheng-by-keepal/
[C_ dfs_01]: https://leetcode-cn.com/problems/target-sum/solution/c-dfshe-01bei-bao-by-bao-bao-ke-guai-liao/
[2_0-1]: https://leetcode-cn.com/problems/target-sum/solution/bei-bao-da-qia-ti-20-1bei-bao-qia-hao-zhuang-man-b/
[494. 1]: https://leetcode-cn.com/problems/target-sum/solution/494-mu-biao-he-by-ming-zhi-shan-you-m9rfkvkdad/
[Python3 DFS _ 01_ _ _]: https://leetcode-cn.com/problems/target-sum/solution/python-dfs-xiang-jie-by-jimmy00745/
[98_java]: https://leetcode-cn.com/problems/target-sum/solution/dong-tai-gui-hua-ji-bai-liao-98de-javayong-hu-by-r/