递归优化的这三种方式你知道吗？

痛定思痛。 2022-11-29 12:43 116阅读 0赞

估计找工作的，都会碰到面试官老是问道“递归算法”，感同身受，前段时间面试的时候，就有一家问道这个问题，是非常典型的问题。在前面一篇[世界上有哪些代码量很少，但很牛逼很经典的算法或项目案例？][Link 1]，递归应该算是比较“经典”的算法。

## 1.从 斐波那契数列开始说起 ##

波那契数列指的是这样一个数列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144，是指这样一个数列

递推公式如图：

![format_png][] 递推公式

有没有直接计算的公式？当然有![format_png 1][]

public int Fibo(int n)
    {
        double c = Math.Sqrt(5);
        return (int)((Math.Pow((1 + c) / 2, n) - Math.Pow((1 - c) / 2, n)) / c);
    }

## 1.最常见的递归 ##

第一项和第二项的值均为1，后面每项的值都是前两项值之和，所以我们很多人基本上都会使用递归来实现，常见的算法如下：

public int Fibo(int n)
            {
               if (n == 1 || n == 2)
               {
                    return 1;
               }
               return Fibo(n - 2) + Fibo(n - 1);
            }

但这种做法并不能完全解决问题，因为最大允许的递归深度跟当前线程剩余的栈空间大小有关，事先无法计算。如果实时计算，代码过于复杂，就会影响代码的可读性。所以，如果最大深度比较小，比如 10、50，就可以用这种方法，否则这种方法并不是很实用。

ps：递归代码要警惕重复计算

除此之外，使用递归时还会出现重复计算的问题。刚才我讲的第二个递归代码的例子，如果我们把刚才我讲的第二个递归代码的例子，如果我们把整个递归过程分解一下的话，那就是这样的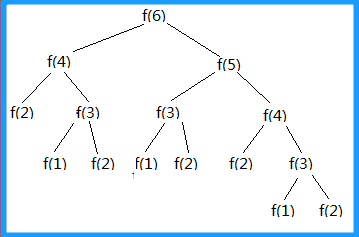：![format_png 2][]`n 越大，这段代码执行效率越低`通过测试一下看他的效率如何

Stopwatch sw = new Stopwatch();
                sw.Start();
                var result = Fibo(40);
                sw.Stop();
                Debug.WriteLine("n=100；result="+result+"；耗时："+sw.ElapsedMilliseconds);

n=10；result=55；耗时：2715
    n=40；result=102334155；耗时：4673

如果n再稍微大一点，所消耗的时间是成指数级增长的，比如n=64的时候，所消耗的时间可能是两三年！不信的话，你可以试试！

我们会发现f(n)这个方法被调用了很多次，而且其中重复率非常之高，也就是说被重复计算了很多次，如果n稍微大一点这棵树会非常庞大。这里我们可以看出，每个节点就需要计算一次，总计算的次数就是该二叉树节点的数量，可见其时间复杂度为O(2n)，是指数级的，其空间复杂度也就是该二叉树的高度，为O(n)。这样来看，我们应该就清楚了，为什么这段代码效率如此低下了吧。

## 2.数组保存法 ##

我们应该避免无数次重复的计算

为了避免无数次重复，可以从n=1开始往上计算，并把每一个计算出来的数据，用一个数组保存，需要最终值时直接从数组中取即可，算法如下：

public int fib(int n) {
        int[] fib = new int[n];
        fib[0] = 1;
        fib[1] = 1;
        for (int i = 2; i < n; i++) {
            fib[i] = fib[i - 2] + fib[i - 1];
        }
        return fib[n - 1];
    }

测试一下结果

n=10；result=55；耗时：0
    n=40；result=102334155；耗时：0
    n=1000000；result=1884755131；耗时：5

毫秒级，几乎忽略不计的，当计算100万时，也就5毫秒

## 3.滚动数组法 ##

尽管上述算法已经很高效了，但我们还是会发现一个问题，其实整个数组中，每次计算时都只需要最新的3个值，前面的值计算完后就不再需要了。比如，计算到第10次时，需要的数组空间只有第8和第9两个空间，前面第1到第7个空间其实就不再需要了。所以我们还可以改进，通过3个变量来存储数据，算法如下：

public int Fibo3(int n)
            {
                int first = 1;
                int second = 1;
                int third = 2;
                for (int i = 3; i <= n; i++)
                {
                    third = first + second;
                    first = second;
                    second = third;
                }
                return third;
            }

时间复杂度仍然为O(n)，而空间复杂度为常量级别3，即空间复杂度为0，所以这种方法是非常高效的。

## 3.尾递归法 ##

首先我们来了解一下什么是尾调用。

> 在计算机科学里，尾调用是指一个函数里的最后一个动作是一个函数调用的情形：即这个调用的返回值直接被当前函数返回的情形。这种情形下该调用位置为尾位置。

/// n 第n个数
     /// first 第n个数
     /// second 第n与第n+1个数的和
     /// @return 返回斐波那契数列值
    public int Fib5(int n, int first, int second) {
        if (n <= 1) {
            return first;
        } else {
            return fib5(n-1,second,first+second);
        }
    }

，也都是通过两个变量保存计算值，传递给下一次进行计算，递归的过程中也是根据n值变化逐步重复运算，和循环差不多，时间复杂度和空间复杂度也都一样,优雅了很多。

我们知道递归调用是通过栈来实现的，每调用一次函数，系统都将函数当前的变量、返回地址等信息保存为一个栈帧压入到栈中，那么一旦要处理的运算很大或者数据很多，有可能会导致很多函数调用或者很大的栈帧，这样不断的压栈，很容易导致栈的溢出。

还有一种优化思路就是矩阵快速幂法，可参考链接 https://blog.csdn.net/computer\_user/article/details/86927209

![format_png 3][]

**回复** **【关闭】**学关闭微信朋友圈广告

**回复** **【实战】**获取20套实战源码

**回复** **【福利】**获取最新微信支付有奖励

**回复** **【被删】**学查看你哪个好友删除了你巧

**回复** **【访客】**学微信查看朋友圈访客记录

**回复** **【卡通】**学制作微信卡通头像

**回复** **【python】**学微获取全套0基础Python知识手册

**回复** **【2019】**获取2019 .NET 开发者峰会资料PPT

[![format_png 4][]][format_png 4 1]

[winform已死？这8个Winform开源项目还有多少人在用？][format_png 4 1]

[![format_png 5][]][format_png 5 1]

[VS Code 1.47 发布！官方版 Settings Sync 终于来了！][format_png 5 1]

[![format_png 6][]][format_png 6 1]

[张善友：最新.NET程序员省份分布排名][format_png 6 1]

[![format_png 7][]][format_png 7 1]

[Pandownload关闭了，百度网盘真的提速高达10Mb/s?][format_png 7 1]

[Link 1]: http://mp.weixin.qq.com/s?__biz=MzIxNjIwNzQ5Mw%3D%3D&chksm=8f883d65b8ffb4739b080285907c08779c0e51cbbb5854af66305352d21514b3c3c8736193ae&idx=1&mid=2649752719&scene=21&sn=2990240e22919d2388995b94b8680c6b#wechat_redirect
[format_png]: /images/20221124/48eb861081ba4a22acca4b40ec1bebcc.png
[format_png 1]: /images/20221124/6552e8735e9548f4b7a2d15079fec96f.png
[format_png 2]: /images/20221124/2b52c129d42244f7bbe697d9c8671917.png
[format_png 3]: /images/20221124/55fd3bd8aef840ac93051f2259482353.png
[format_png 4]: /images/20221124/016361b28be04b629d6f22432a48211a.png
[format_png 4 1]: http://mp.weixin.qq.com/s?__biz=MzIxNjIwNzQ5Mw%3D%3D&chksm=8f8835e1b8ffbcf7e188b0e4de1f33292f3bf6200071571d0a8f14ce95e8f05acfe902c07f0c&idx=1&mid=2649754635&scene=21&sn=124a8ee50f4bf495d81b4f48f17e062b#wechat_redirect
[format_png 5]: /images/20221124/0d8e9f97367e45c48092ace99d44edb8.png
[format_png 5 1]: http://mp.weixin.qq.com/s?__biz=MzIxNjIwNzQ5Mw%3D%3D&chksm=8f883204b8ffbb125a21191c5c8997e47441c0054cecae8324783f1f7a6c9f497ea6f40677a9&idx=1&mid=2649754606&scene=21&sn=98048b18aff01d207a5560ae3ddd657c#wechat_redirect
[format_png 6]: /images/20221124/bcfa7c577a9e4f2f893e74dff1b97107.png
[format_png 6 1]: http://mp.weixin.qq.com/s?__biz=MzIxNjIwNzQ5Mw%3D%3D&chksm=8f883046b8ffb950ed6c0846718efd5645bcaa2e93d14d273a7015d5a9805637923b5d346ab3&idx=1&mid=2649754028&scene=21&sn=3f94a0c5272f8aa2a52ed95c0f324db5#wechat_redirect
[format_png 7]: /images/20221124/33641ff1b65a4a3da8c4cf5ae508d530.png
[format_png 7 1]: http://mp.weixin.qq.com/s?__biz=MzIxNjIwNzQ5Mw%3D%3D&chksm=8f883041b8ffb95751cd9d9b1b0fdd163f22859213fa65023a8472615b9a750942d8aa06b0b1&idx=1&mid=2649754027&scene=21&sn=6235da5f1c2ce47b662d675646cbbeab#wechat_redirect