排序算法原理及实现

ゞ浴缸里的玫瑰 2022-11-16 08:21 141阅读 0赞

### 排序算法原理及实现 ###

*  插入排序
 *   *  原理：
     *  实现：
 *  希尔排序
 *   *  原理：
     *  实现：
 *  选择排序
 *   *  原理：
     *  实现：
 *  冒泡排序
 *   *  原理：
     *  实现：
 *  堆排序
 *   *  原理：
     *  实现：
 *  快速排序
 *  归并排序
 *  排序算法的性能分析

排序，使一串记录，基于比较，按照递增或者递减的排列起来。  
通常意义上的排序，都是原地排序（in place sort）

# 插入排序 #

## 原理： ##

我们将整个区间看做无序区间和有序区间，每次选择无序区间的第一个元素，然后在有序区间的合适位置插入。  
![在这里插入图片描述][20210406194112834.png]

## 实现： ##

public static void insertSort(long[] array) { 
            for (int i = 1; i < array.length; i++) { 
            //[0,i)有序
            //[i,array.length)无序
                long t = array[i];
                int j;
                for (j = i - 1; j >= 0 && array[j] > t; j--) { 
                    array[j + 1] = array[j];
                }
                array[j + 1] = t;
            }
        }

ps：因为左边是有序区间，每次插入需要找到其位置，我们可以使用折半查找的方式找到其所需要插入的位置。

public static void insertSort2(long[] array) { 
            for (int i = 1; i < array.length; i++) { 
                long t = array[i];
                int left = 0;
                int right = i;
                //[left,right)
                while (left < right) { 
                    int mid = (left + right) / 2;
                    if (t >= array[mid]) { 
                        left = mid + 1;
                    } else { 
                        right = mid;
                    }
                }
    
                for (int j = i; j > left; j--) { 
                    array[j] = array[j - 1];
                }
                array[left] = t;
            }
        }

# 希尔排序 #

## 原理： ##

希尔排序的原理可以简单来说，将一组待排的数据，按次序依次分为若干组，然后在每一组中进行插入排序，分组每次减少，当分组为1的时候，再进行一次插入排序。  
如图：相同颜色分为一组，进行插排，然后在分组，继续插排…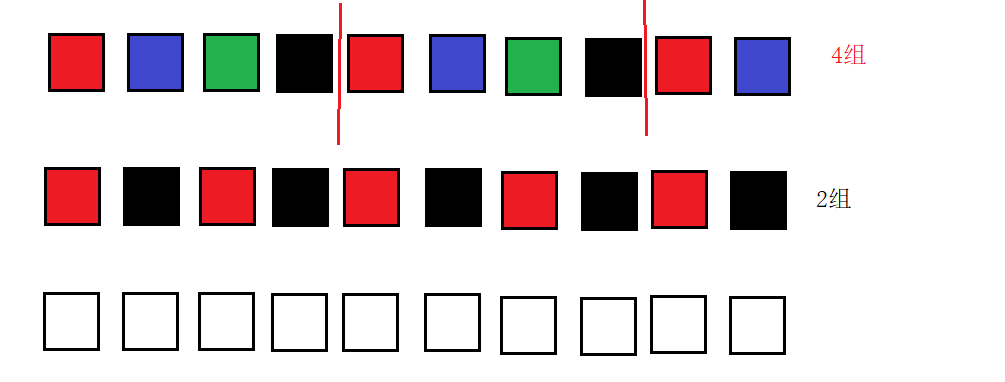  
![在这里插入图片描述][watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl81MjE0MjczMQ_size_16_color_FFFFFF_t_70]

## 实现： ##

public class ShellSort { 
        public static void shellSort(long[] array) { 
            int gap = array.length;
            while (gap > 1) { 
                insertSortGap(array, gap);
                gap = gap / 2;
            }
            insertSortGap(array, 1);
        }
    
        private static void insertSortGap(long[] array, int gap) { 
            for (int i = 1; i < array.length; i++) { 
                long t = array[i];
                int j = i - gap;
                for (; j >= 0 && array[j] > t; j -= gap) { 
                    array[j + gap] = array[j];
                }
                array[j + gap] = t;
            }
        }
    }

# 选择排序 #

## 原理： ##

每一次从无序区间中选择出最大（最小）的一个元素，放入有序区间的最后面（最前面），直到全部排完。

## 实现： ##

public static void selectSort(long[] array) { 
            for (int i = 0; i < array.length - 1; i++) { 
                int max = 0;
                for (int j = 1; j < array.length - i; j++) { 
                    if (array[j] > array[max]) { 
                        max = j;
                    }
                }
                Swap.swap(array, max, array.length - i - 1);
            }
        }

# 冒泡排序 #

## 原理： ##

每走一趟，将最大（最小）的元素放在最后面，走（n-1）趟就能有序。

## 实现： ##

public static void bubbleSort(long[] array) { 
            for (int i = 0; i < array.length - 1; i++) { 
                boolean flg = true;
                for (int j = 0; j < array.length - i - 1; j++) { 
                    if (array[j] > array[j + 1]) { 
                        Swap.swap(array, j, j + 1);
                        flg = false;
                    }
                }
                if (flg){ 
                    break;
                }
            }
        }

# 堆排序 #

## 原理： ##

基本原理和选择排序相同，但是区别就是不通过遍历寻找最大（最小）的元素，而是通过建堆，然后将无序区间最大（最小）的元素找出来。  
（建堆——将头尾交换——向下调整）  
排升序要建大堆，排降序要建小堆

## 实现： ##

public class HeapSort { 
        public static void heapSort(long[] array) { 
            creatHeap(array);
            for (int i = 0; i < array.length - 1; i++) { 
                Swap.swap(array, 0, array.length - i - 1);
                shiftDown(array, array.length - i - 1, 0);
            }
        }
    
        //建堆
        private static void creatHeap(long[] array) { 
            for (int i = (array.length - 2) / 2; i >= 0; i--) { 
                shiftDown(array, array.length, i);
            }
    
        }
    
        //向下调整
        private static void shiftDown(long[] array, int size, int index) { 
            //建小堆
            while (true) { 
                int leftIndex = 2 * index + 1;
                if (leftIndex >= size) { 
                    return;
                }
                int maxIndex = leftIndex;
                int rightIndex = leftIndex + 1;
                if (rightIndex < size && array[rightIndex] > array[leftIndex]) { 
                    maxIndex = rightIndex;
                }
                if (array[maxIndex] < array[index]) { 
                    return;
                }
                long t = array[index];
                array[index] = array[maxIndex];
                array[maxIndex] = t;
                index = maxIndex;
            }
        }
    }

# 快速排序 #

关于快速排序相对较复杂，请点击传送门：

链接：[快速排序][Link 1]

# 归并排序 #

关于归并排序详情，请点击传送门：

链接：[归并排序][Link 2]

# 排序算法的性能分析 #

关于各个算法，时间复杂度、空间复杂度总结分析：

链接：[性能分析][Link 3]

[20210406194112834.png]: /images/20221022/595b6fe69085410a937b2187443c3cc2.png
[watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl81MjE0MjczMQ_size_16_color_FFFFFF_t_70]: /images/20221022/1321375eb0c041c4b44c3d0e62ea142a.png
[Link 1]: https://blog.csdn.net/weixin_52142731/article/details/115485640
[Link 2]: https://blog.csdn.net/weixin_52142731/article/details/115498361
[Link 3]: https://blog.csdn.net/weixin_52142731/article/details/115530273