深度学习知识总结—— 3. 激活函数与非线性输出（Activation function and Nonlinear Output）

红太狼 2022-10-13 05:28 146阅读 0赞

在前面的章节里，分别介绍了声名远扬的梯度下降算法，计算图，以及反向传播。现在我们要思考这样一个问题。对于 y = a x + b y = ax +b y=ax+b这样一个线性模型来说，无论x有多复杂，都无法改变它线性输出的特点。
线性模型对于线性问题的求解是可行，但是我们需要用倒神经元网络的实际应用场景来说，有很多是无法直接套用线性模型来求解的。举个例子来说，对于分类问题，就无法很好的依靠线性模型进行求解。
所以，为了解决这个问题，就有科学家提出在每一层神经元的输出上，根据需要套一个激活函数，从而破坏神经元的线性结构，使它有求解非线形问题的能力。

文章目录

  • 关于激活函数与非线性输出
  • 在线性模型上增加激活函数
  • 常见的几个激活函数
    • Sigmoid 函数
    • tanh 函数
    • ReLu 函数
  • 来做个简单的应用吧
  • 后记

关于激活函数与非线性输出

首先，我们先弄清楚一个问题。在实际的应用场景中输入的参数可能有多个，比如以经典的机器学习样本集鸢尾花为例

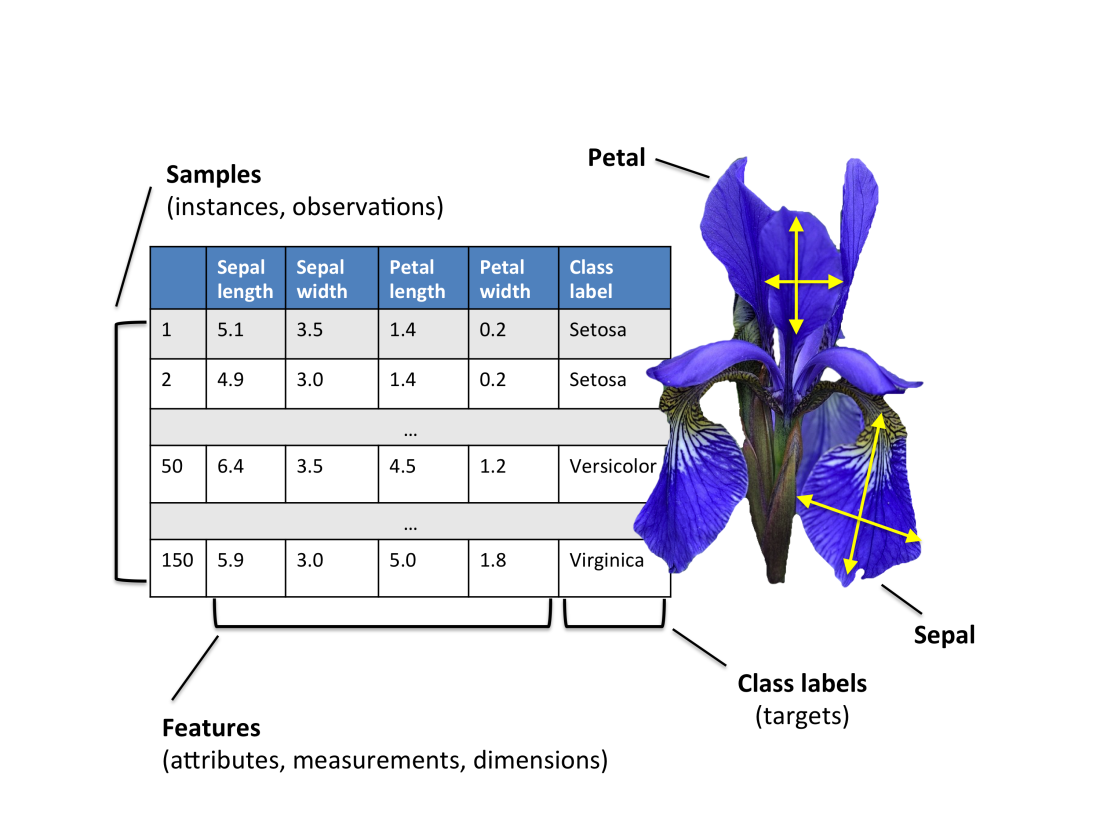
在这里插入图片描述
每个样本就最少包含4个基本属性（Features），以及对鸢尾花的分类(Class label)。由于实际生活中，很多问题不是非黑即白的，具有一定的模糊空间。例如，对于温水和热水，37度如果觉得还算温水，那么38度呢，39度呢。

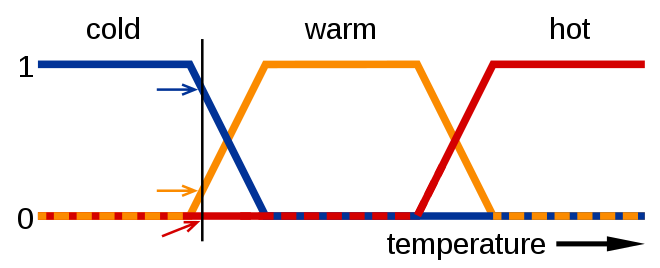
在这里插入图片描述
而对于我们的数据集鸢尾花也有这样的情况。

在这里插入图片描述
这张图是关联性分析，可以看到在以萼片、花瓣大小进行分析品种时，会有“粘黏”的情况。所以可以知道如果线性的对数据进行类别判定，会出现非常大的偏差。所以我们需要对模型进行适当的“弯折”，让它的输出不要那么过于线性。

所以，使用激活函数的目的，就是为了影响计算图每一层的输出，打破输出值与输入参数之间的线性关系。你可以理解为在每一层的输出过程中加入一点“玄学”的元素。

在线性模型上增加激活函数

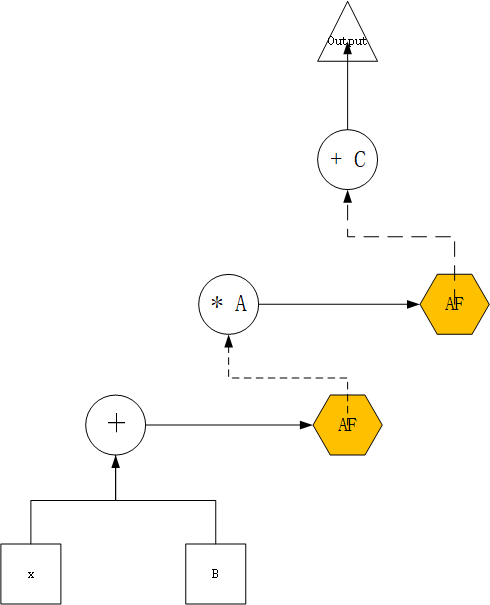
在这里插入图片描述
如果说原来的线性计算模型是这样的：

Created with Raphaël 2.3.0随机输入权重向前传播并更新参数损失函数->符合期望？输出权重向后传播并更新权重yesno

那么增加了激活函数的模型就变成了这样：

Created with Raphaël 2.3.0随机输入权重向前传播并更新参数通过激活函数映射到新函数空间损失函数->符合期望？输出权重向后传播并更新权重yesno

由于激活函数的存在，使得输出不再是简简单单的线性输出，你不必担心由于新增了激活函数后，导致原模型中梯度的消失。事实上你可以类比一下 normalize 这种操作（在图形图像上很常见，比如把原始数据转换成浮点后经过滤波等操作后，为了可视化，需要把处理后的数据重新映射到[0, 255]的区间），梯度经过新函数变换后依然保留。

那么我们常用的激活函数有哪些呢？

常见的几个激活函数

Sigmoid 函数

严格来说，Sigmoid函数不止一个，任何符合 σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1+ e^{-x}} σ(x)=1+e−x1​函数图像的，都可以被归类为Sigmoid函数，这是一种经常被用来做 0-1 分类问题的函数。

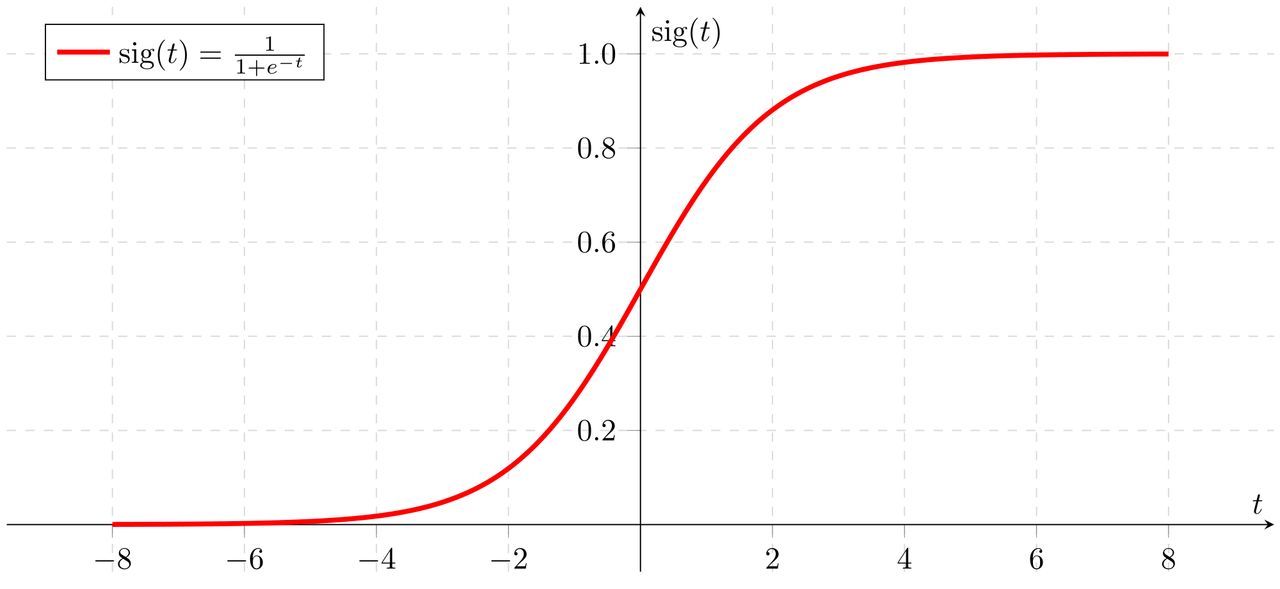
在这里插入图片描述

其函数式写为：

σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1+ e^{-x}} σ(x)=1+e−x1​

除它之外，还有比较相似的tanh函数，其输出图像是：

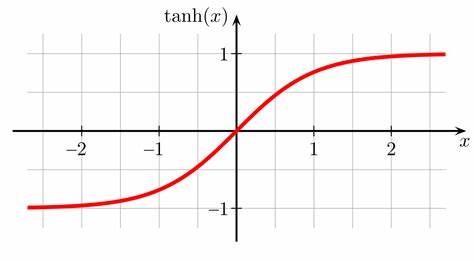
在这里插入图片描述
这一类的都是Sigmoid函数家族，但是一般提到Sigmoid，一般指的就是老大哥 σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1+ e^{-x}} σ(x)=1+e−x1​了。

这类函数的优点：

在于它可导，并且值域在有限范围区间，如 [0, 1]，可以使神经元的输出标准化。

缺点：

  • 容易导致梯度消失：例如它的函数值在趋近 0 和 1 的时候函数值会变得平坦，梯度趋近于 0。
  • 不以零为中心：函数的输出恒为正值，不是以零为中心的，这会导致权值更新时只能朝一个方向更新，从而影响收敛速度。
  • 计算成本高昂：exp() 函数与其他非线性激活函数相比，计算成本高昂。
  • 梯度爆炸：x值在趋近0的左右两边时，会造成梯度爆炸情况。

tanh 函数

属于Sigmoid函数的一种，但是和老大哥所不同，它的取值范围是 [-1, 1]
在这里插入图片描述
其函数式为：

σ ( x ) = e x − e − x e x + e − x \sigma(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} σ(x)=ex+e−xex−e−x​

缺点和Sigmoid函数一样，但是优点是解决了Sigmoid只能在[0, 1]之间的问题，其取值范围是[-1 , 1]

ReLu 函数

有些地方叫它整流函数，它可以对神经元输出进行有针对性的数据过滤作用。比方说，数据经过一定的处理后，输出的值包含符号为正的有效数据和符号为负的噪音数据，为了避免噪音数据输入到下一层的网络，所以可以使用这个函数，过滤需要的数据。

从函数图像上看，它是分段函数，基本的ReLu函数的函数式表达为：

σ ( x ) = { 0 x < 0 x x ≥ 0 \sigma(x) =\left\{\begin{matrix} 0 & x < 0\\ x & x \geq 0\\ \end{matrix}\right. σ(x)={ 0x​x<0x≥0​

当然，这个方向并不固定，根据需要也可以反过来，例如

σ ( x ) = { 0 x > 0 x x ≤ 0 \sigma(x) =\left\{\begin{matrix} 0 & x > 0\\ x & x \leq 0\\ \end{matrix}\right. σ(x)={ 0x​x>0x≤0​
在这里插入图片描述
常见的是最左侧的。但是有时候总有人想适当放一些另外一侧的数据，所以提出了其他的改进形式。

优点：

  • 收敛速度快
  • 能够滤除不需要的噪音
  • 降低运算成本

缺点：

  • 和Sigmoid函数相似，单向性
  • 如果在负轴存在有效数据，由于梯度消失的原因，而无法有效收敛

即便改进型避免了负轴的梯度归零的问题，但是ReLu存在的缺点，实际上只是得到了轻微修正而已，可以说这个系列的激活函数是缺点和优点都十分突出的函数家族。

来做个简单的应用吧

假设我们有这么一张表，这是一张我比较喜欢的辉光管工作时长表，这种前苏联时代的老玩意由于适用寿命都不长，所以如果持续点亮，那么在一定时候就会坏掉。

在这里插入图片描述


















































Duration(Year.) Work
0.1 True
0.3 True
0.5 True
0.7 True
0.9 True
1.1 True
1.3 True
1.5 False
1.7 False
1.9 False

也就是说，当时间到1.5年后，辉光管一定会坏掉，那么问题是1.4年的时候，它坏掉的机率有多大？

我们用Torch来执行一下，首先使用一个线性模型对数据进行预测，并且为了增加一点玄学的成分，用Sigmoid作为激活函数，BCE函数作为损失函数，然后看看预测情况如何

  1. import torch
  3. x_data = torch.Tensor([[0.1], [0.3], [0.5], [0.7], [0.9], [1.1], [1.3], [1.5], [1.7], [1.9]])  # 1 column x 10 rows
  4. y_data = torch.Tensor([[1], [1], [1], [1], [1], [1], [1], [0], [0], [0]])  # 0 - false, 1 - true
  7. class SimpleLogisticModel(torch.nn.Module):
  9.     def __init__(self):
  10.         super().__init__()
  11.         self.linear = torch.nn.Linear(1, 1)
  12.         """ Regression analysis of the data was continued using the linear model """
  14.     def forward(self, x):
  15.         y_predicted = torch.sigmoid(self.linear(x))
  16.         return y_predicted
  19. if __name__ == "__main__":
  20.     # fitting modle
  21.     model = SimpleLogisticModel()
  23.     # LOSS function
  24.     criterion = torch.nn.BCELoss(size_average=False)
  26.     # parameters optimizer
  27.     optimizer = torch.optim.SGD(model.parameters(), lr=0.1)  # stochastic gradient descent
  29.     # training and do gradient descent calculation
  30.     for epoch in range(500):
  31.         # forward
  32.         # y_predict_value = model(x_data)
  33.         y_predicted_value = model.forward(x_data)
  35.         # use MSE to check the deviation
  36.         loss = criterion(y_predicted_value, y_data)
  38.         # print for debug
  39.         print(epoch, loss.item())
  41.         # set calculated gradient to zero
  42.         optimizer.zero_grad()
  44.         # call backward to update the parameters
  45.         loss.backward()
  47.         # optimize parameters
  48.         optimizer.step()
  50.     # finally
  51.     print("omega = ", model.linear.weight.item())
  52.     print("bias = ", model.linear.bias.item())
  54.     # test values
  55.     x_test = torch.Tensor([1.4])
  56.     y_test = model(x_test)
  58.     # print out result
  59.     print("final y = ", y_test.data)

输出结果是：

  1. omega =  -7.137760162353516
  2. bias =  9.893336296081543
  3. final y =  tensor([0.4751])

如果四舍五入，那么y = 0，也就是说1.4年后，坏掉的可能性是53%，其实概率还是挺大的呢～

后记

如果你刚接触Ai框架，你可能看到这里有点懵，这些函数都是干嘛的，有什么用。其实我计划把如何使用这些Ai框架的内容放在后面，这部分属于理论范畴，我们弄明白神经元是怎么工作的先。

另外，关于激活函数就我介绍的这么些吗？其实目前公布的有很多，这里只是提到了一些对于初学者来说常用和简单的类型。在某乎上有这么一个帖子目前总结了目前常用的激活函数总类，你可以去那帖子上面看看。

发表评论

表情：
评论列表 （有 0 条评论，146人围观）

还没有评论，来说两句吧...

相关阅读