二叉树的创建和相关算法

水深无声 2022-08-22 13:25 252阅读 0赞

Center

二叉树是一种非常重要的数据结构，它是分支结构的基础，今天本人将写一篇博客来叙述一下其相关的算法以及二叉树的创建过程！

1：二叉树的创建：

主要有 先序，中序，后序，层序创建几种方式，其中前三种建立在二叉树遍历方式的基础上的。

（1）：先序创建

先序创建就是先创建根节点，随后依次创建其左子树和右子树，我们可以采用递归的方法来实现，因为二叉树本身就是建立在递归算法的基础上的。

（2）：中序和后序创建：

明白了前序创建二叉树的方式，中序和后续我们也可以类比出来，所谓前中后序，就是创建根节点的顺序而已。

（3）：层序遍历和创建：

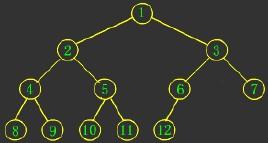
：Center 1

以上图片反映的层序遍历的过程，层序遍历是建立在队列的基础上的，首先如果一颗二叉树非空，让根节点入队，如果根节点的左子树后右子树非空，则根节点出队并打印它的数据域的值，左右子树先后入队（谁不空谁入队），随后就是一个递归的过程了。

可见层序遍历是从上到下，从左到右的一个遍历过程。

所以我们也可以层序创建一个二叉树：首先创建根节点，如果根节点的左孩子和右孩子指针没有指向虚结点，则创建左子树和右子树，也是通过递归的方式来创建的。

二叉树代码：

函数文件 Bittree.c: 

  1. #include "Bittree.h"
  2. #include <stdio.h>
  3. #include <stdlib.h>
  4. #include <assert.h>
  6. tree *Creat(tree* root, tree*(*ptree)(tree *root))
  7. {
  8.     root = ptree(root);
  9.     return root;
  10. }
  11. tree *Tier_creat(tree* root)   //层序创建二叉树    root为根节点
  12. {
  14.     tree *s = NULL;
  15.     datatype data = 0;
  16.     tree *Tree_arr[MAX] = { 0 };       //创建一个存储二叉树结点的队列
  17.     int front = 1;                     //front为队列指针初值
  18.     int rear = 0;                      //rear为队列末尾指针初值
  19.     printf("层数创建二叉树，以-1表示虚结点，-2表示结束！\n");
  20.     scanf("%d", &data);
  21.     while (data != -2)
  22.     {
  23.         s = NULL;
  24.         if (data != -1)
  25.         {
  26.             s =(tree*) malloc(sizeof(tree)* 1);
  27.             s->data = data;
  28.             s->Lchild = NULL;
  29.             s->Rchild = NULL;
  30.         }
  31.         rear++;
  32.         Tree_arr[rear] = s;           //双亲节点入队
  33.         if (rear == 1) root = s;      //如果rear为队头指针，则其队列中存储的为二叉树的根节点
  34.         else
  35.         {
  36.             if (Tree_arr[rear] && s)     //孩子和双亲都不是虚结点
  37.             {
  38.                 if (rear % 2 == 0)   Tree_arr[front]->Lchild = s;        //新节点是左孩子
  39.                 if (rear % 2 == 1)
  40.                 {
  41.                     Tree_arr[front]->Rchild = s;    //新节点是右孩子
  42.                     front++;                        //如果是此时rear指向右孩子，则出队，下一个节点进队
  43.                 }
  44.             }
  45.         }
  46.         scanf("%d", &data);
  47.     }
  48.     return root;
  49. }
  50. tree *DLR_creat(tree* root)    //先序创建二叉树
  51. {
  52.     printf("以-1表示指针域为空，以-2表示结束创建过程\n");
  53.     root = NULL;
  54.     int data = 0;
  55.     printf("请输入数据：");
  56.     scanf("%d", &data);
  57.     if (data == -1)
  58.         return NULL;
  59.     root = (tree*)malloc(sizeof(tree)* 1);
  60.     if (root == NULL)
  61.          {
  62.             printf("创建失败！\n");
  63.             exit(EXIT_FAILURE);
  64.          }
  65.      root->data = data;
  66.      root->Lchild=DLR_creat(root->Lchild);
  67.      root->Rchild = DLR_creat(root->Rchild);
  68.      return root;
  69. }
  70. tree *LDR_creat(tree* root)    //中序创建二叉树
  71. {
  72.     printf("以-1表示指针域为空，以-2表示结束创建过程\n");
  73.     root = NULL;
  74.     int data = 0;
  75.     printf("请输入数据：");
  76.     scanf("%d", &data);
  77.     if (data == -1)
  78.         return NULL;
  79.     root->Lchild = DLR_creat(root->Lchild);
  80.     root = (tree*)malloc(sizeof(tree)* 1);    
  81.     if (root == NULL)
  82.     {
  83.         printf("创建失败！\n");
  84.         exit(EXIT_FAILURE);
  85.     }
  86.     root->data = data;
  87.     root->Rchild = DLR_creat(root->Rchild);
  88.     return root;
  89. }
  90. tree *RLD_creat(tree* root)    //后序创建二叉树
  91. {
  92.     printf("以-1表示指针域为空，以-2表示结束创建过程\n");
  93.     root = NULL;
  94.     int data = 0;
  95.     printf("请输入数据：");
  96.     scanf("%d", &data);
  97.     if (data == -1)
  98.         return NULL;
  99.     root->Lchild = DLR_creat(root->Lchild);
  100.     root->Rchild = DLR_creat(root->Rchild);    
  101.     root = (tree*)malloc(sizeof(tree)* 1);
  102.     if (root == NULL)
  103.     {
  104.         printf("创建失败！\n");
  105.         exit(EXIT_FAILURE);
  106.     }
  107.     root->data = data;
  108.     return root;
  109. }
  110. void Print_Tree(tree *root, void(*ptree)(tree *root))  //遍历二叉树
  111. {
  112.     assert(root);
  113.     if (root == NULL)
  114.     {
  115.         printf("树是空树！\n");
  116.         return;
  117.     }
  118.     else
  119.     {
  120.         ptree(root);
  121.         printf("\n");
  122.     }
  123. }
  124. void DLR_Print(tree *root)      //先序遍历二叉树
  125. {
  127.     if (root != NULL)
  128.     {    
  129.         printf("%d  ", root->data);
  130.         DLR_Print(root->Lchild);
  131.         DLR_Print(root->Rchild);
  132.     }
  133.     return;
  135. }
  136. void LDR_Print(tree *root)      //中序遍历二叉树
  137. {
  139.     if (root != NULL)
  140.     {
  141.         DLR_Print(root->Lchild);
  142.         printf("%d  ", root->data);
  143.         DLR_Print(root->Rchild);
  144.     }
  145.     return;
  146. }
  147. void RLD_Print(tree *root)      //后序遍历二 叉树
  148. {
  150.     if (root != NULL)
  151.     {
  152.         DLR_Print(root->Lchild);
  153.         DLR_Print(root->Rchild);
  154.         printf("%d  ", root->data);
  155.     }
  156.     return;
  157. }
  158. void Tie_Print(tree *root)             //层序遍历二叉树
  159. {
  160.     tree* arry[MAX] = { 0 };
  161.     int rear = 1;
  162.     int front = 0;
  163.     if (root == NULL)
  164.     {
  165.         printf("二叉树为空！\n");
  166.         return;
  167.     }
  168.     else
  169.     {
  170.         arry[0] = root;                    //如果二叉树不为空，根节点先入队。
  171.         while (front < rear)               //循环条件   队列非空
  172.         {
  173.             if (arry[front])
  174.             {
  175.                 printf("%d ", arry[front]->data);
  176.                 arry[rear++] = arry[front]->Lchild;
  177.                 arry[rear++] = arry[front]->Rchild;
  178.                 front++;
  179.             }
  180.             else
  181.             {
  182.                 front++;
  183.             }
  184.         }
  185.     }
  186. }
  188. int Deep_tree(tree *root)     //求二叉树的深度
  189. {
  190.     assert(root);
  191.     int left = 0;
  192.     int right = 0;
  193.     int deep = 0;
  194.     if (root != NULL)
  195.     {
  196.         left=Deep_tree(root->Lchild);             //求左子树深度
  197.         right = Deep_tree(root->Rchild);          //求右子树深度
  198.         deep = left > right ? (left + 1) : (right + 1);
  199.     }
  200.     return deep;
  201. }
  202. int Node_du(tree *root)      //求某个节点的度
  203. {
  204.     assert(root);
  205.     int ret = 0;
  206.     if (root == NULL)
  207.         return 0;
  208.     else
  209.     {
  210.         if (root->Lchild != NULL)
  211.             ret++;
  212.         if (root->Rchild != NULL)
  213.             ret++;
  214.         return ret;
  215.     }
  216. }
  218. int tree_Node(tree *root)
  219. {
  220.     assert(root);
  221.     int ret = 0;
  222.     if (root == NULL)
  223.         return 0;
  224.     if (root->Lchild == NULL&&root->Rchild == NULL)        //叶子节点
  225.         return 1;
  226.     ret =1+ tree_Node(root->Lchild) + tree_Node(root->Rchild);
  227.     return ret;
  228. }
  230. tree* search_Node(tree *root, datatype data)                //查找值为data的节点
  231. {
  232.     assert(root);
  233.     tree *p=NULL;
  234.     if (root == NULL)
  235.     {
  236.         printf("树是空树！\n");
  237.         return NULL;
  238.     }
  239.     else
  240.     {
  241.         if (root->data == data)
  242.             return root;
  243.         if (root->Lchild != NULL)
  244.         {
  245.             p = search_Node(root->Lchild,data);
  246.             if (p != NULL)
  247.                 return p;
  248.         }
  250.         if (root->Rchild != NULL)
  251.         {
  252.             p = search_Node(root->Rchild,data);
  253.             if (p != NULL)
  254.                 return p;
  255.         }
  256.         return NULL;   //没找到返回空
  257.     }
  258. }
  260. void Deal_tree(tree *root)   //释放内存
  261. {
  262.     assert(root);
  263.     if (root == NULL)
  264.         return;
  265.     Deal_tree(root->Lchild);
  266.     Deal_tree(root->Rchild);
  267.     free(root);
  268.     root = NULL;
  269. }

头文件 Bittree.h 

  1. #ifndef __BITTREE_H__
  2. #define __BITTREE_H__
  3. #define _CRT_SECURE_NO_WARNINGS
  4. #define MAX  100
  5. typedef int datatype;
  6. typedef struct Bittree
  7. {
  8.     datatype data;
  9.     struct Bittree *Lchild;
  10.     struct Bittree *Rchild;
  12. }tree;
  13. typedef struct
  14. {
  15.     datatype Elem_data[MAX];
  16.     int length;
  17. }Tree_arry;
  18. tree *Tier_creat(tree* root);   //层序创建二叉树    root为根节点
  19. tree *DLR_creat(tree* root);    //先序创建二叉树
  20. tree *LDR_creat(tree* root);    //中序创建二叉树
  21. tree *RLD_creat(tree* root);    //后序创建二叉树
  22. tree *Creat(tree* root,tree*(*ptree)(tree *root));     //创建二叉树
  23. void Print_Tree(tree *root, void(*ptree)(tree *root));  //遍历二叉树
  24. void DLR_Print(tree *root);      //先序遍历二叉树
  25. void LDR_Print(tree *root);      //中序遍历二叉树
  26. void RLD_Print(tree *root);      //后序遍历二叉树
  27. void Tie_Print(tree *root);      //层序遍历二叉树
  28. int Deep_tree(tree *root);       //求二叉树的深度
  29. int Node_du(tree *root);          //求某个节点的度
  30. int tree_Node(tree *root);       //求树的节点的个数
  31. tree* search_Node(tree *root, datatype data);                //查找值为data的节点
  32. void Deal_tree(tree *root);       //释放内存
  34. #endif __BITTREE_H__

测试文件test.c:

  1. #include "Bittree.h"
  2. #include <stdio.h>
  3. #include <stdlib.h>
  4. void Init()
  5. {
  6.     printf("1:二叉树的创建\n");
  7.     printf("2:二叉树的遍历\n");
  8.     printf("3:二叉树的深度查询\n");
  9.     printf("4:二叉树的某一个节点的度的查询\n");
  10.     printf("5:清空二叉树\n");
  11.     printf("0:退出\n");
  12. }
  13. void Init_Print()
  14. {
  15.     printf("0：层序遍历二叉树.\n");
  16.     printf("1：先序遍历二叉树.\n");
  17.     printf("2：后序遍历二叉树.\n");
  18.     printf("3：中序遍历二叉树.\n");
  19. }
  20. void Init_Creat()
  21. {
  22.     printf("0：层序创建二叉树.\n");
  23.     printf("1：先序创建二叉树.\n");
  24.     printf("2：后序创建二叉树.\n");
  25.     printf("3：中序创建二叉树.\n");
  26. }
  27. void  test()
  28. {
  29.     int ret;
  30.     int key=0;
  31.     int choose;
  32.     datatype data=0;
  33.     tree *root = NULL;
  34.     tree *node = NULL;
  35.     tree* (*Tree_C[4])(tree *root) = { 0 };   //函数指针数组存放二叉树的创建方式
  36.     void(*Tree_p[4])(tree *root) = { 0 };   //函数指针数组存放二叉树的遍历方式
  37.     Tree_C[0] = Tier_creat;
  38.     Tree_C[1] = DLR_creat;
  39.     Tree_C[2] = LDR_creat;
  40.     Tree_C[3] = RLD_creat;
  41.     Tree_p[0] = Tie_Print;
  42.     Tree_p[1] = DLR_Print;
  43.     Tree_p[2] = LDR_Print;
  44.     Tree_p[3] = DLR_Print;
  45.     while (1)
  46.     {
  47.         printf("请输入你的选择：");
  48.         scanf("%d", &key);
  49.         switch (key)
  50.         {
  51.         case 0:
  52.             printf("Program Over!!\n");
  53.             exit(EXIT_FAILURE);
  54.             break;
  55.         case 1:
  56.             Init_Creat();
  57.             do
  58.             {
  59.                 printf("请输入你的选择：");
  60.                 scanf("%d", &choose);
  61.             } while (choose <= 0 && choose >= 3);
  62.             root = Creat(root, Tree_C[choose]);
  63.             break;
  64.         case 2:
  65.             Init_Print();
  66.             do
  67.             {
  68.                 printf("请输入你的选择：");
  69.                 scanf("%d", &choose);
  70.             } while (choose <= 0 && choose >= 3);
  71.             Print_Tree(root, Tree_p[choose]);
  72.             break;
  73.         case 3:
  74.             ret = Deep_tree(root);
  75.             printf("二叉树的深度为：%d\n", ret);
  76.             break;
  77.         case 4:
  78.             printf("请输入你要查询节点所保存的数据：");
  79.             scanf("%d", &data);
  80.             node=search_Node(root, data);
  81.             if (node == NULL)
  82.             {
  83.                 printf("你所要查询的节点不存在！\n");
  84.                 exit(EXIT_FAILURE);
  85.             }
  86.             ret = Node_du(node);
  87.             printf("数据为%d的节点的度为：%d\n",data, ret);
  88.             break;
  89.         case 5:
  90.             Deal_tree(root);
  91.             printf("清空成功！\n");
  92.             break;
  93.         }
  94.     }
  95. }
  97. int main()
  98. {
  99.     Init();
  100.     test();
  101.     system("pause");
  102.     return 0;
  103. }

如果上述叙述有相关问题请大家能指出，本人邮箱：597995302@qq.com

发表评论

表情：
评论列表 （有 0 条评论，252人围观）

还没有评论，来说两句吧...

相关阅读

    相关 二叉树相关的算法题思想

    二叉树是面试经常会考到的一个知识点，关于二叉树延伸的应用也很广泛。二叉树的核心是递归，但我们在遇到二叉树相关的问题时，如果纠结于递归这个点，很可能陷进去，毕竟人的大脑装不下那么

    落日映苍穹つ落日映苍穹つ/ 0 赞/ 236 阅读

    相关 二叉树的创建和相关算法

    ![Center][] 二叉树是一种非常重要的数据结构，它是分支结构的基础，今天本人将写一篇博客来叙述一下其相关的算法以及二叉树的创建过程！ 1：二叉树的创建： 主要有

    水深无声水深无声/ 0 赞/ 253 阅读

    相关 二叉树的创建

    二叉树的层序创建 创建步骤： 概括：队列里面出一个元素，输入两个元素作为这个元素的左右结点，然后将这两个元素中不为0的元素接着入队列 1. 先输入第一个数据，如果第

    电玩女神电玩女神/ 0 赞/ 304 阅读

    相关 iOS 二叉树相关算法实现

    什么是二叉树？ 在计算机科学中，二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”和“右子树”，左子树和右子树同时也是二叉树。二叉树的子树有左右之分，并且次

    桃扇骨桃扇骨/ 0 赞/ 373 阅读