完全二叉树/ 满二叉树/二叉树遍历（前序、中序、后序、层序遍历）-蒲公英云

完全二叉树/ 满二叉树/二叉树遍历（前序、中序、后序、层序遍历）

1.概念

在计算机科学中，二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有2^{i-1}个结点；深度为k的二叉树至多有2^k-1个结点；对任何一棵二叉树T，如果其终端结点数为n_0，度为2的结点数为n_2，则n_0=n_2+1。一棵深度为k，且有2^k-1个节点称之为满二叉树；深度为k，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中，序号为1至n的节点对应时，称之为完全二叉树。

二叉树在图论中是这样定义的：二叉树是一个连通的无环图，并且每一个顶点的度不大于3。有根二叉树还要满足根结点的度不大于2。有了根结点之后，每个顶点定义了唯一的父结点，和最多2个子结点。然而，没有足够的信息来区分左结点和右结点。如果不考虑连通性，允许图中有多个连通分量，这样的结构叫做森林。

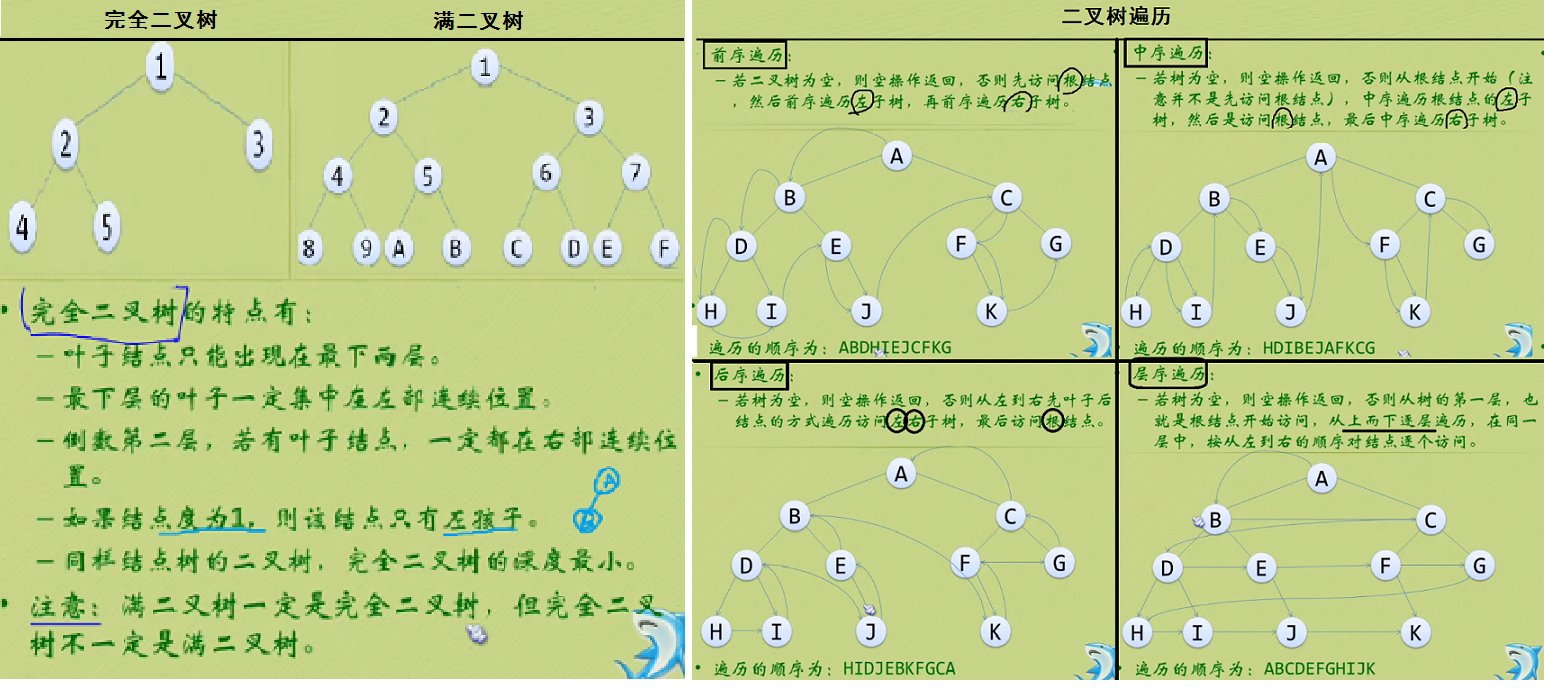
(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

Center

2.代码

//Implementation code for Binary Tree
//功能：按照约定，以前序遍历的方法输入数据，输出数据所在层数
//递归依次赋值:
//根结点 - 左结点 - 右结点（前序遍历法）
//左结点 - 根结点 - 右结点（中序遍历法）
//左结点 - 右结点 - 根结点（后序遍历法）
#include <stdio.h>
#include <stdlib.h>
//#include <string>
typedef char ElemType;
typedef struct BiTNode           //定义二叉树结点
{
    char data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
char string[100];
//创建一颗二叉树，约定用户遵循的前序遍历方式输入数据
void CreateBiTree(BiTree *T)
{
    char c;
    scanf("%c", &c);
    if (' ' == c)
    {
        *T = NULL;               //递归终止条件
    }
    else
    {
        *T = (BiTNode*)malloc(sizeof(BiTNode));
        (*T)->data = c;
        //递归依次赋值 此处：根结点-左结点-右结点（前序遍历法）
        CreateBiTree(&(*T)->lchild);
        CreateBiTree(&(*T)->rchild);
    }
}
void visit(char c, int level)
{
    printf("%c 位于第 %d 层 \n", c, level);
}
//遍历二叉树
//参数  T  : 要遍历的二叉树
//参数level: 遍历开始的层数
void PreOrderTraverse(BiTree T, int level)
{    
    if (T)                       //遍历终止条件 NULL
    {
        visit(T->data, level);   //递归：根 - 左 - 右
        PreOrderTraverse(T->lchild, level + 1);
        PreOrderTraverse(T->rchild, level + 1);
    }
}
int main()
{
    int level = 1;
    BiTree T = NULL;
    CreateBiTree(&T);
    PreOrderTraverse(T, level);
    return 0;
}