【数据结构与算法】二叉树的遍历（递归遍历、非递归遍历、层序遍历）-蒲公英云

导读：

二叉树递归遍历
二叉树非递归遍历
层次遍历

二叉树是一种非常重要的数据结构，很多其他数据结构都是基于二叉树的基础演变过来的。二叉树的遍历有前序、中序、后序三种，由于数的本身就是就是递归定义的，因此可以采用递归方法遍历但其开销也较大。若采用非递归实现遍历，则需要采用栈实现，递归本身也是用栈实现的。而二叉树的层序遍历是按照每一层进行遍历，很明显需要用队列来辅助实现。下面先介绍二叉树的三种递归遍历，然后再介绍三种非递归遍历，最后介绍层序遍历。

二叉树的定义如下：

public class BTNode {
    public int data;
    public BTNode left   = null;    //左孩子节点
    public BTNode right  = null;    //右孩子节点
    public BTNode() { }
    public BTNode(int data) {
        this.data = data;
    }
}

一、二叉树前序、中序、后序的递归实现

1、前序遍历：根节点—左孩子—右孩子

/*
     * 前序递归遍历二叉树
     */
    public static void preOrder(BTNode tree) {
        if (tree != null) {
            System.out.print(tree.data + " ");
            preOrder(tree.left);
            preOrder(tree.right);
        }
    }

2、中序遍历：左孩子—根节点—右孩子

/*
     * 中序递归遍历
     */
    public static void inOrder(BTNode tree) {
        if(tree != null) {
            inOrder(tree.left);
            System.out.print(tree.data+" ");
            inOrder(tree.right);
        }
    }

3、后序遍历：左孩子—根节点—右孩子

/*
     * 后序递归遍历
     */
    public static void postOrder(BTNode tree) {
        if(tree != null) {
            postOrder(tree.left);
            postOrder(tree.right);
            System.out.print(tree.data+" ");
        }
    }

二、二叉树前序、中序、后序的非递归实现

以下面的二叉树为例，来分析非递归的实现过程。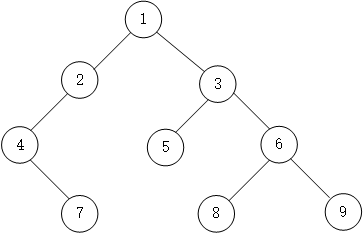
这里写图片描述

遍历的结果：
前序遍历： 1 2 4 7 3 5 6 8 9
中序遍历： 4 7 2 1 5 3 8 6 9
后序遍历： 7 4 2 5 8 9 6 3 1

【Tips】：对于每个节点，都当作根节点的情况来分析。

1、前序遍历的非递归实现
实现思路如下：
对于任一节点p：
（1）如果p不为空，则输出节点p，然后将其入栈，让p指向其左孩子节点；
（2）如果p为空，如果栈非空则让栈顶元素出栈，但不输出，让出栈元素指向其右孩子节点。

遍历过程如下：（刚开始p指向根节点1）
（1）节点1非空，则输出节点1，将节点1入栈，让p指向节点1的左孩子节点2；（栈中元素：1）
（2）节点2非空，则输出节点2，将节点2入栈，让p指向节点1的左孩子节点4；（栈中元素：1 2）
（3）节点4非空，则输出节点4，将节点4入栈，让p指向节点4的左孩子节点；（栈中元素：1 2 4）
（4）节点4的左孩子节点为空，则取出栈顶元素，即节点4出栈，让p指向节点4的右孩子节点7；（栈中元素：1 2）
（5）节点7非空，则输出节点7，将节点7入栈，让p指向节点7的左孩子节点；（栈中元素：1 2 7）
（6）节点7的左孩子节点为空，则取出栈顶元素节点7，让p指向节点7的右孩子节点；（栈中元素：1 2）
（7）节点7的右孩子节点为空，则取出栈顶元素节点2，由于节点2的右孩子也为空，继续取出栈顶元素节点1，让p指向节点1的右孩子；（栈中元素：null）
（8）此时按照上面的规则遍历节点1的右子树……

至此可以得到前序遍历结果： 1 2 4 7 3 5 6 8 9

代码如下：

/*
     * 前序非递归遍历二叉树
     */
    public static void preOrder2(BTNode tree) {
        Stack<BTNode> stack = new Stack<>();    //定义一个空栈，用于保存遍历过的元素
        BTNode curr = tree;        //定义指向当前节点的节点
        //直到当前节点curr为null且栈空时，循环结束 
        while(curr != null || !stack.isEmpty()) {
            if (curr != null) {        //当前节点不为空则遍历该节点
                System.out.print(curr.data + " ");
                stack.push(curr);
                curr = curr.left;
            } else {    //当前节点为空则出栈，遍历右孩子节点
                curr = stack.pop();
                curr = curr.right;
            }
        }
    }

2、中序遍历的非递归实现
中序的遍历过程和前序一样，只是节点的输出位置不一样。

代码如下：

/*
     * 中序非递归遍历。（遍历思路和前序差不多，只是输出位置不一样）
     */
    public static void inOrder2(BTNode tree) {
        Stack<BTNode> stack = new Stack<>();
        BTNode curr = tree;
        while (curr != null || !stack.isEmpty()) {
            if (curr != null) {        //该节点不为空则将节点入栈，并指向其左孩子节点
                stack.push(curr);
                curr = curr.left;
            } else {  //节点为空则从栈中取出元素，输出，并指向其右孩子节点
                curr = stack.pop();
                System.out.print(curr.data + " ");
                curr = curr.right;
            }
        }
    }

3、后序遍历的非递归实现
后序遍历的非递归是三种非递归实现中比较复杂的，关键点在于对于一个节点，需要分别考虑该节点是左孩子节点还是右孩子节点。如果是左孩子节点，则需要先遍历父节点的右子树，再遍历父节点；如果是右孩子节点，则直接遍历其父节点。

实现思路如下：
（1）若树非空，则将树的根节点入栈，并依次判断节点是否有左孩子，若有则全部入栈；
若栈非空，则循环以下步骤，
（2）取出栈顶元素p；
（3）如果p的右孩子节点为空，或者p的右孩子节点上次已经访问，则输出节点p；
（4）否则，暂时不能访问该节点，将其入栈，并指向其右孩子，将右孩子的左子树的左孩子节点全部入栈；

代码如下：

/*
     * 后序非递归遍历
     */
    public static void postOrder2(BTNode tree) {
        Stack<BTNode> stack = new Stack<>();
        BTNode curr = tree;
        BTNode lastVisited = null;      //记录上次访问的节点
        //把curr移到左子树的最下边
        while(curr != null) {
            stack.push(curr);
            curr = curr.left;
        }
        while(!stack.isEmpty()) {
            curr = stack.pop();
            //访问根节点的两种情况：1，右孩子节点为空；2，右孩子节点是上次访问的节点
            if (curr.right == null || curr.right == lastVisited) {
                System.out.print(curr.data + " ");
                lastVisited = curr;        //修改最近被访问的节点
            } else {  //右子树没有被访问且不为空
                //由于根节点存在右子树没有访问，则根节点需再次入栈
                stack.push(curr);
                //进入右子树
                curr = curr.right;
                while(curr != null) {
                    stack.push(curr);
                    curr = curr.left;
                }
            }
        }
    }

三、层序遍历

层序遍历由于其层级的关系，遍历的过程也就比较容易，主要是从左到右，自上而下，依次将二叉树的各节点入队。

实现思路如下：
（1）若树非空，先将树的根节点入队；
若队列非空，则循环以下步骤，
（2）取出队头元素并输出；
（3）若该队头元素有左孩子，则将其左孩子入队；
（4）若该队头元素有右孩子，则将其右孩子入队。

代码如下：

/*
     * 层序遍历
     */
    public static void levelOrder(BTNode tree) {
        LinkedList<BTNode> queue = new LinkedList<>();    //用链表来定义一个队列
        if (tree != null) {
            queue.offer(tree);    //根结点入队
            while(!queue.isEmpty()) {
                BTNode p = queue.poll();    //取出队头元素
                System.out.print(p.data + " ");
                if (p.left != null) {    //若左孩子不为空，则入队列
                    queue.offer(p.left);
                }
                if (p.right != null) {    //若右孩子不为空，则入队列
                    queue.offer(p.right);
                }
            }
        }
    }

【参考资料】

[1] 苏叔叔，二叉树前序、中序、后序遍历非递归写法的透彻解析。http://blog.csdn.net/zhangxiangdavaid/article/details/37115355
[2] 兰亭风雨，【数据结构与算法】二叉树递归与非递归遍历。http://blog.csdn.net/ns_code/article/details/12977901