python实现二叉搜索树

深碍√TFBOYSˉ_ 2022-05-30 08:51 196阅读 0赞

class Node(object):
        def __init__(self,data=None):
            self._left=None #左节点
            self._right=None #右节点
            self._data=data
        #一系列get set方法
        def set_left(self,node):
            self._left=node
        def set_right(self,node):
            self._right=node
        def get_left(self):
            return self._left
        def get_right(self):
            return self._right
        def set_data(self,data):
            self._data=data
        def get_data(self):
            return self._data
    
    class Binary_tree(object):
        def __init__(self,root):#这个根要是Node的对象
            self.__in_order=[]#中序遍历的列表
            self.__pre_order=[]#前序遍历的列表
            self.__post_order=[]#后序遍历的列表
            self.__root=root
        #下面带有help的都是私有函数
        def __preorder_help(self,root):#利用递归进行前序遍历
            if root:
                self.__pre_order.append(root.get_data())
                self.__preorder_help(root.get_left())
                self.__preorder_help(root.get_right())
            return self.__pre_order
        def __inorder_help(self,root):#利用递归进行中序遍历
            if root:
                self.__inorder_help(root.get_left())
                self.__in_order.append(root.get_data())
                self.__inorder_help(root.get_right())
            return self.__in_order
        def __postorder_help(self,root):#利用递归进行后序遍历
            if root:
                self.__postorder_help(root.get_left())
                self.__postorder_help(root.get_right())
                self.__post_order.append(root.get_data)
            return self.__post_order
        def preorder(self):
            return self.__preorder_help(self.__root)
        def inorder(self):
            return self.__inorder_help(self.__root)
        def postorder(self):
            return self.__postorder_help(self.__root)
    #貌似纯二叉树没什么卵用，就不写示列了。
    #二叉搜索树就不一样了，下面会有示列。
    
    class BSTNode(Node):
        def __init__(self,data=None):
            Node.__init__(self,data=data)#这继承不像c++,不会默认调用父类的构造函数，需要像这样写
            self.__in_order=[]#中序遍历的列表
            self.__pre_order=[]#前序遍历的列表
            self.__post_order=[]#后序遍历的列表
        def insert(self,data):
            if data<self._data:#比此数据小就插左边，否则就插右边
                if self._left:
                    return self._left.insert(data)
                else:
                    self._left=BSTNode(data)
            else:
                if self._right:
                    return self._right.insert(data)
                else:
                    self._right=BSTNode(data)
        @staticmethod#静态方法
        def min_val_bst_node(bst_node):
            current=bst_node
            while current._left is not None:
                current=current._left
            return current
        def delete(self,data):
            if self is None:#发现没有这个数据时做以下处理
                return None
            if data<self._data:#要删的数据比此数据小，就从左子树删起
                self._left=self._left.delete(data)
            elif data>self.get_data():#要删的数据比此数据大，从右子树删起
                self._right=self._right.delete(data)
            else:#要删的就是此数据
                if self._left is None:#当左子树为空时，返回右子树，那么这个数据就删掉了，返回上层的时候，它的父节点与右子树相连
                    temp=self._right
                    return temp
                elif self._right is None:#当右子树为空，与上面相似
                    temp=self._left
                    return temp
            #如果左右子树都不为空时，把右子树的最左节点（最小结点）和此结点的数据替换
            temp = self.min_val_bst_node(self._right)
            self._data=temp._data
            self._right=self._right.delete(temp._data)
            return self
        def find(self,data):
            if data==self.get_data():
                return True
            elif data<self.get_data():#小就往左子树找，大就往右子树找
                if self._left:
                    return self._left.find(data)
                else:
                    return False
            else:
                if self.get_right():
                    return self._right.find(data)
                else:
                    return False
        #下面这些函数与纯二叉树的类似
        def inorder(self,root):
            if root:
                self.inorder(root._left)
                self.__in_order.append(root._data)
                self.inorder(root._right)
            return self.__in_order
    
        def preorder(self,root):
            if root:
                self.__pre_order.append(root._data)
                self.preorder(root._left)
                self.preorder(root._right)
            return self.__pre_order
        def postorder(self,root):
            if root:
                self.postorder(root._left)
                self.postorder(root._right)
                self.__post_order.append(root._data)
            return self.__post_order
    
    class BST(object):
        def __init__(self):
            self.__root=None
        def insert(self,data):
            if self.__root:
                self.__root.insert(data)
            else:
                self.__root = BSTNode(data)
    
        def delete(self,data):
            if self.__root:
                return self.__root.delete(data)
    
        def find(self,data):
            if self.__root:
                return self.__root.find(data)
            else:
                return False
    
        def preorder(self):
            if self.__root:
                return self.__root.preorder(self.__root)
        def inorder(self):
            if self.__root:
                return self.__root.inorder(self.__root)
    
        def postorder(self):
            if self.__root:
                return self.__root.postorder(self.__root)
    
        def __numbers_of_nodes_help(self,root):
            if root:
                return self.__numbers_of_nodes_help(root._left)+self.__numbers_of_nodes_help(root._right)+1
            else:
                return 0
        def numbers_of_nodes(self):
            return self.__numbers_of_nodes_help(self.__root)
    
    my_list=[8,5,10,2,6,9,11]
    bst=BST()
    for e in my_list:
        bst.insert(e)
    print("中序遍历：",bst.inorder())
    print("后序遍历：",bst.postorder())
    print("前序遍历：",bst.preorder())
    print("结点数：",bst.numbers_of_nodes())
    #剩下的功能可以自己尝试

输出：

中序遍历： [2, 5, 6, 8, 9, 10, 11]
    后序遍历： [2, 6, 5, 9, 11, 10, 8]
    前序遍历： [8, 5, 2, 6, 10, 9, 11]
    结点数： 7

对了，那个二叉搜索树的图是这样的：

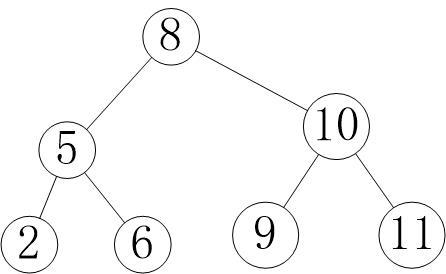
![20180308180045166][]

[20180308180045166]: /images/20220530/2c1385390abc4a8eb8eb15522559b456.png