基于经纬度的空间距离计算--空间统计

小灰灰 2022-05-23 06:28 192阅读 0赞

# 空间统计–基于经纬度的空间距离计算 #

设空间划分为若干区块，每个区块给一个标号z ，如 1,2,...,Z  1 , 2 , . . . , Z ,其区号可根据邮政编码、医院ID号划分。设空间区块 i,j  i , j 的坐标或经纬度为(xi,yi)(xj,yj)  ( x i , y i ) ( x j , y j )  之间的距离为 Lij  L i j  ，则在平面坐标 系下可用两点间距离公式计算，若是较大区域，则应使用地图的经纬度球面距离公式来计算。  
计算具体分析：  
已知两点经纬度，求取两点距离，当距离不远时，可用平面近似算法。设经度 为a度，纬度为b度，A 点经纬度为A=(a1,b1  a 1 , b 1 ),B点经纬度为A=(a2,b2  a 2 , b 2 ),则AB两点沿东西方向上的距离为：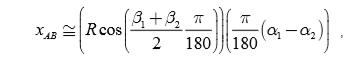  
![这里写图片描述][70]  
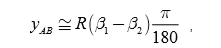
AB两点沿南北方向上的距离：![这里写图片描述][70 1]  
![这里写图片描述][70 2]  
其中R为地球半径，可取6371.004千米或 6371km （地球赤道半径 6378.140 千米地球极地半径 6356.755 千米）。 AB 两点的直线距离可估算为 :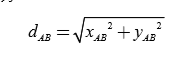  
![这里写图片描述][70 3]

以下为JAVA实现已知两点经纬度求地理直线距离：

//已知两点经纬度求地理直线距离
    public static void main(String[] args) {  
    
        //地球半径   
        double R=6378137.0;   
        //模拟数据  
        double lat1=109.99309;  
        double log1=39.81625;  
        double lat2=109.99456;  
        double log2= 39.81595;  
        //将角度转化为弧度  
        double radLat1=(lat1*Math.PI/180.0);  
        double radLat2=(lat2*Math.PI/180.0);  
        double radLog1=(log1*Math.PI/180.0);  
        double radLog2=(log2*Math.PI/180.0);  
        //纬度的差值  
        double a=radLat1-radLat2;  
        //经度差值  
        double b=radLog1-radLog2;  
        //弧度长度  
        double s=2*Math.asin(Math.sqrt(Math.pow(Math.sin(a/2), 2)+Math.cos(radLat1)*Math.cos(radLat2)*Math.pow(Math.sin(b/2), 2)));  
        //获取长度  
        s=s*R;  
        //返回最接近参数的 long。结果将舍入为整数：加上 1/2  
        s=Math.round(s*10000)/10000;  
        System.out.println(s);  
    }

结果为：  
![这里写图片描述][70 4]

[70]: /images/20220523/7aad76447a65454ca6d6c326ad05135d.png
[70 1]: /images/20220523/95a7168f9e0c4985a67b280429f9a5d2.png
[70 2]: /images/20220523/e9569192b4a8480dbbf53fe3d001e2a4.png
[70 3]: /images/20220523/cf53c982c7ff44d18b4d369739ad6f0d.png
[70 4]: /images/20220523/c3ee171547c845aea41eb7e31c49f877.png