二叉树三种遍历方式(递归和非递归)-蒲公英云

树形结构是一类重要的非线性数据结构。其中以树和二叉树是最为常用。

二叉树有四种遍历顺序：先序遍历(前序遍历)，中序遍历，后序遍历，层序遍历。

这三种遍历的方式其实是由遍历的根结点的顺序来定义的。

先序遍历：先访问根结点，再遍历它的左子树，最后遍历它的右子树。

中序遍历：先遍历左子树，然后访问根结点，最后遍历它的右子树。并且在遍历左右子树的时候。仍然是先遍历左子树，然后访问根节点，最后遍历右子树。

后序遍历：先遍历左子树，然后遍历右子树，最后访问根结点。在遍历左右子树的时候同样要先遍历左子树，然后遍历右子树，最后访问根节点。

层序遍历：从上往下逐层进行遍历。

来看一个例子：

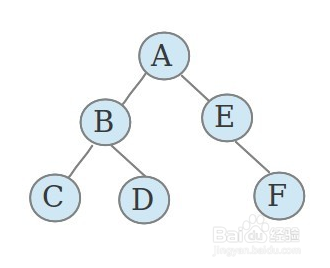
先定义二叉树的每个结点的数据域和指针域：

struct node{
    int v; //数据域
    node *lson; //当前节点的左子结点
    node *rson;//当前节点的右子结点
};

上图所示就是一棵二叉树，那么现在来遍历这棵二叉树。

先序遍历：根据前面所述先序遍历的定义，就会先遍历A，输出A，然后遍历A的左子结点B，输出B，此时又会将B看成一棵新的二叉树的根结点，再遍历B的左子结点C，输出C，发现C没有任何子结点了，就会回到B，再遍历B的右子结点D，输出D，发现D没有任何子结点了，然后回到A，再遍历A的右子结点，输出E，然后发现E没有左子结点，回到E，继续遍历E的右子结点F，输出F，最后发现F没有任何子结点了，至此，先序遍历结束，所得到的结果就是ABCDEF。

中序遍历：先来到根结点A，然后遍历它的左子树，来到结点B，再遍历B的左子树，到结点C，继续遍历C的左子树，发现没有，然后返回到结点C，输出C，再遍历C的右子树，发现也没有，然后回到结点B，输出B，再遍历B的右子树，来到结点D，继续遍历D的左子树，没有，然后回到D，输出D，再遍历D的右子树也没有，然后回到D，B的左右子树已遍历完，再返回上一层到结点A，此时，A的左子树已经全部遍历完，所以访问根结点，输出A，再开始遍历A的右子树，来到E，遍历E的左子树，发现为空，返回E，输出E，再遍历E的右子树，到F，遍历F的左子树，发现为空，返回到F，输出F，再遍历F的右子树，同样为空，又返回F，然后E的子树也遍历完，返回A，至此，中序遍历结束，所得到的结果是CBDAEF。

后序遍历：先到根结点A，然后遍历它的左子树，来到结点B，再遍历B的左子树，到结点C，继续遍历C的左子树，发现没有，然后返回到结点C，再遍历C的右子树，发现也没有，然后返回到结点C，输出C，再遍历B的右子树，来到结点D，继续遍历D的左右子树，发现均为空，于是返回到D，输出D，B的左右子树遍历完，又返回到B，输出B，A的左子树已遍历完，然后遍历A的右子树，到结点E，遍历E的左子树，发现为空，返回到E，再遍历E的右子树，来到F，遍历F的左右子树，发现均为空，返回到F，输出F，然后E的左右子树均已遍历完，有返回到E，输出E，此时A的左右子树已遍历完，回到A，输出A，至此，后续遍历结束，得到的结果为CDBFEA。

层序遍历：从上往下从左往右依次遍历，结果就是ABECDF。

接下来给出三种遍历方式的递归版代码：

先序遍历：

void preOrder(node *root)
{
    if(root == NULL) return;
    cout<<root->v<<" ";
    preOrder(root->lson);
    preOrder(root->rson);
}

中序遍历：

void inOrder(node *root)
{
    if(root == NULL) return;
    inOrder(root->lson);
    cout<<root->v<<" ";
    inOrder(root->rson);
}

后序遍历：

void posOrder(node *root)
{
    if(root == NULL) return;
    posOrder(root->lson);
    posOrder(root->rson);
    cout<<root->v<<" ";
}

下面给出三种遍历方式的非递归版：

先序遍历：

1.申请一个空栈，将祖先结点压入栈中。

2.弹出栈顶元素，因为是先序遍历，所以直接输出这个栈顶元素。因为是先序遍历的遍历顺序是根—>左—>右，但是因为栈是先进后出，所以应该先推入右子结点，再推入左子结点(如果有左子结点和右子结点的话)。

3.不断重复第2步，直到栈为空。

void preOrder(node *root)
{
    stack<node*>sk;
    while(!sk.empty()) sk.pop();
    sk.push(root);
    while(!sk.empty()){
        node *cur = sk.top();//栈顶元素是当前的结点
        sk.pop();//弹出栈顶元素
        cout<<cur->v<<" ";
        if(cur->rson!=NULL) sk.push(cur->rson);
        if(cur->lson!=NULL) sk.push(cur->lson);
    }
}

中序遍历：

1.申请一个空栈，将祖先结点压入栈中。

2.如果当前结点不为空，就将结点压入栈，然后让结点变为当前结点的左子结点。如果当前结点为空，就取出栈顶元素并打印，然后弹出栈顶元素，再让当前结点变为当前结点的右子结点。

3.不断重复第2步，直到栈空并且当前结点为空的时候。

void Inorder(node *root)
{
    stack<node*>sk;
    while(!sk.empty()) sk.pop();
    while(!sk.empty() || root!=NULL){
        if(root == NULL){
            node *cur = sk.top();
            sk.pop();
            cout<<cur->v<<" ";
            root = cur->rson;
        }else{
            sk.push(root);
            root = root->lson;
        }
    }
}

后序遍历：

1.创建两个空栈，一个栈保存结点元素，一个栈保存输出的答案。

2.如果栈不为空，就弹出存结点元素的栈顶记为cur，然后将栈顶元素出栈，并且将cur压入存储答案的栈中，如果cur有左子结点就将左子结点压入存结点元素的栈中，如果有右子结点，也将右子结点压入这个栈中。

3.重复第2步，直到栈空。

void posOrder(node *root)
{
    stack<node*>sk; //保存结点元素
    stack<node*>res; //保存输出的元素
    while(!sk.empty()) sk.pop();
    while(!res.empty()) res.pop();
    sk.push(root);
    while(!sk.empty()){
        node *cur = sk.top();
        sk.pop();
        res.push(cur);
        if(cur->lson != NULL) sk.push(cur->lson);
        if(cur->rson != NULL) sk.push(cur->rson);
    }
    while(!res.empty()){
        cout<<res.top()->v<<" ";
        res.pop();
    }
}