数据结构与算法简述递归算法-蒲公英云

数据结构与算法简述递归算法

港控/mmm° 2022-03-31 13:58 345阅读 0赞

递归就是函数（方法）不断调用自身，直到得到想要的结果。

其思路是把一个大问题转化为规模很小的子问题，这些子问题性质一样，可以采用同一种方式处理，通过解决小问题来达到解决大问题的目的。

典型使用递归的有计算阶乘，汉诺塔问题等，递归有三要素：1明确的终止条件，不能一直递归下去，2终止处理办法，3能提取重复的逻辑，简单化问题。

计算阶乘

/**
 * 递归
 * 阶乘
 */
public class Factorial {
    /**
     * 计算n的阶乘
     */
    public int factorial(int n) {
        if(n == 1) {
            return 1;
        }
        return n * factorial(n-1);
    }
    public static void main(String[] args) {
        Factorial f = new Factorial();
        System.out.println(f.factorial(4));
    }
}

汉诺塔问题

源于印度古老历史，三根柱子，有n个从小到大的圆盘放在一根柱子上，把所有圆盘移动到另外一个柱子上，并且有如下要求，每次只能移动一个，大圆盘不能在小圆盘之上，移动完之后状态和最初状态一直，上到下是从小到大的次序。

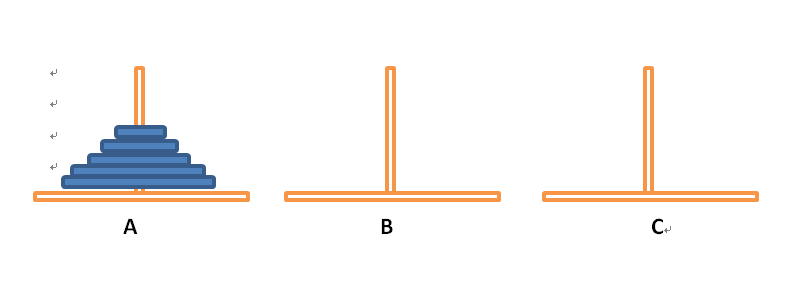
watermark_type_ZmFuZ3poZW5naGVpdGk_shadow_10_text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L2EyODEyNDYyNDA_size_16_color_FFFFFF_t_70

使用递归的分而治之思想来解决问题，假设A柱有n个盘子，先把较小n-1个盘子当成一个整体转移到B柱，再把最后一个盘子移到C柱，依次递归循环下去，C柱为目标柱dest，A和B依次为源柱、临时柱，动态切换

代码实现

/**
 * 递归实现汉诺塔
 */
public class Towers {
    /**
     * 汉诺塔
     * @param topN  待移动圆盘数量
     * @param src     源头柱
     * @param temp    临时柱
     * @param dest    目标柱
     */
    private static void transfer(int topN, String src, String temp, String dest) {
        if(topN == 1) {
            System.out.println(topN + "从" + src + "移动到" + dest);
        } else {
            //把topN-1当成整体，移动到temp柱上
            transfer(topN-1, src, dest, temp);
            //把最大盘移到dest柱上
            System.out.println(topN + "从" + src + "移动到" + dest);
            //把topN-1移动到dest柱上
            transfer(topN-1, temp, src,  dest);
        }
    }
    public static void main(String[] args) {
        transfer(6, "A", "B", "C");
    }
}

背包问题

给定一些大小不一的物品和一个一定容量的背包，如何选择物品把背包刚好装满

/**
 * 背包问题
 */
public class Bags {
    public static void bags(int target,int[] t,int nowIndex,List<Integer> result) {
        if(nowIndex > t.length-1) {    //终止递归
            return;
        }
        if(t[nowIndex] > target) {    //物品比背包大，直接略过
            bags(target, t, nowIndex + 1, result);
        }else if(t[nowIndex] < target){    //物品小于背包，把物品放入背包，减小空余容量，轮询下一物品
            result.add(t[nowIndex]);
            bags(target-t[nowIndex], t, nowIndex+1, result);
        }else{    //物品和背包空余容量大小相等，背包刚好装满，输出结果
            result.add(t[nowIndex]);
            System.out.println(result.toString());
        }
    }
    public static void main(String[] args) {
        int[] t = {11,8,7,5,20,6,9,7};
        for (int i = 0; i < t.length; i++) {
            bags(20, t, i, new ArrayList<>());
        }
    }
}