激活函数知识点汇总-蒲公英云

文章目录

- - 1. 使用激活函数的原因
  - 1. 什么函数才能成为激活函数
  - 3.常用的激活函数
  - - 3.1 sigmoid函数
    - 3.2 tanh 函数
    - 3.3 relu函数
    - 3.4 Elu函数
    - 3.5 Prelu、Leaky ReLU函数
    - 3.6 自归一化激活函数 SELU
  - 1. 如何解决tanh、sigmoid进入非线性饱和区的问题

1. 使用激活函数的原因

没有激活函数，无论神经网络有多少层，输出都是输入的线性组合。
激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

2. 什么函数才能成为激活函数

非线性函数：不管无论神经网络有多少层，输出都是输入的线性组合。退化为线性模型
函数几乎处处可微：保证梯度的可计算性
计算简单：relu比指数型激活函数计算量少
非饱和性：饱和时指某些区间的梯度为零，，relu
单调性：使得梯度方向不会经常改变，从而使训练更容易收敛。
输出范围有限：有限输出使得对一些比较大的输入也有较平稳的表现，这是早期sigmoid比较常用的原因

3.常用的激活函数

3.1 sigmoid函数

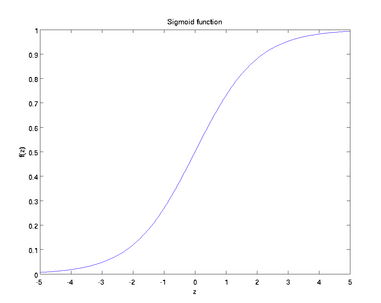在这里插入图片描述 f ( z ) = 1 1 + e x p ( − z ) f (z) = \frac{1}{1+exp(-z)} f(z)=1+exp(−z)1

sigmoid的优点

输出值有限，在0-1之间,有限输出使得对一些比较大的输入也有较平稳的表现
函数光滑可微，导数计算方便

sigmoid的缺点

存在非线性饱和区，容易在方向传播时引起梯度弥散
涉及指数的计算，运算量大，速度不如relu

3.2 tanh 函数

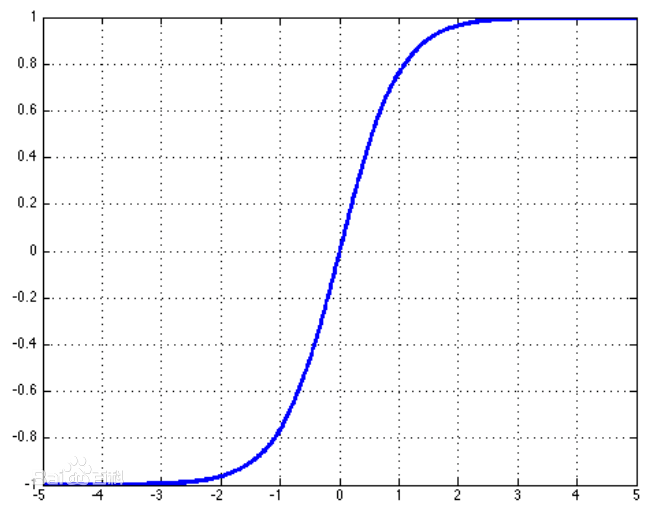在这里插入图片描述 f ( z ) = e z − e − z e z + e − z f (z) = \frac{e^{z}-e^{-z}}{e^{z}+e^{-z}} f(z)=ez+e−zez−e−z

tanh函数的优点

函数光滑可微，导数计算方便
输出值正负对称，稳定在[-1, 1]
具有在0附近梯度较大，有利于区别小的特征差异
tanh函数的缺点
存在非线性饱和区，容易在方向传播时引起梯度弥散
涉及指数的计算，运算量大，速度不如relu

3.3 relu函数

在这里插入图片描述
r e l u （ x ） = m a x ( x , 0 ) relu（x） = max ( x, 0 ) relu（x）=max(x,0)

relu的优点

第一，relu速度更快。采用sigmoid等函数，算激活函数时候（指数运算），计算量大，反向传播求误差梯度时，求导涉及除法，计算量相当大，而采用Relu激活函数，整个过程的计算量节省很多。
第二，对于深层网络，由于sigmoid、tanh函数只在0附近的梯度较大，当趋向两边无穷远时，梯度很小。因此在反向传播时，很容易就出现梯度消失的情况（在sigmoid函数接近非线性饱和区时，变换太缓慢，导数趋于0，这种情况会造成信息丢失），从而无法完成深层网络的训练
第三，Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。

relu的缺点

由于relu函数在负半轴的输出恒为0，这导致relu函数在训练时可能使部分神经元永远不会对数据由激活现象，这个神经元的梯度永远为零，变成一个dead cell。
函数值只能取正值。w的更新方向受到限制，只能往一三象限更新，当最优解在第四象限时，只能更新不能一步到达，只能沿梯子步到达。
也有非线性饱和区问题

注意：如果学习率很大，神经元都”dead”的占比就更多。

3.4 Elu函数

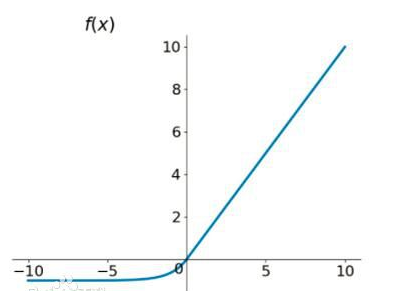
在这里插入图片描述

f ( z ) = { z z > = 0 α ( e z − 1 ) z < 0 f(z) = \left\{\begin{matrix} z& z>=0& \\ \alpha(e^{z}-1) & z<0 & \\end\{matrix\}\\right. f(z)=\{ zα(ez−1)z>=0z<0

优点：
elu函数堆relu进行了改进，使得在输入为负数的情况下，有一定输出。这样可以消除ReLU部分神经元dead的问题。
缺点：

也会陷入非线性饱和区
指数运算复杂度比较高

3.5 Prelu、Leaky ReLU函数

在这里插入图片描述

r e l u （ x ） = α m a x ( x , 0 ) relu（x） = \alpha max ( x, 0 ) relu（x）=αmax(x,0)
优点：

PReLU也是针对ReLU的一个改进型，relu直接乘以一个很小的参数，可以避免ReLU死掉的问题。
相比于ELU，PReLU在负数区域内是线性运算，斜率虽然小，但是不会趋于0，运算量小。
参数α一般是取0~1之间的数，当α=0.01时，成为Leaky ReLU。

3.6 自归一化激活函数 SELU

S E L U ( z ) = λ { z z > = 0 α ( e z − 1 ) z < 0 SELU(z) =\lambda \left\{\begin{matrix} z& z>=0& \\ \alpha(e^{z}-1) & z<0 & \\end\{matrix\}\\right. SELU(z)=λ\{ zα(ez−1)z>=0z<0

优点：

针对ELU的一个改进型，当选取 λ = 1.0506 , α = 1.67326 \lambda = 1.0506, \alpha = 1.67326 λ=1.0506,α=1.67326时，那么SELU(z) 的期望为0，方差为1. 文章中证明，如果使用SELU激活函数，并且初始化权重也为均值为0，方差为1，那么模型具有自归一化属性。自归一化可以在不加入BN的情况下，将每层的数据分布都变成均值为0，方差为1。这样可以：
- 防止过拟合，
- 解决了其他激活函数进入非线性饱和区带来的梯度弥散问题
- 加速模型收敛