C语言实现二叉树的递归遍历与非递归遍历

末蓝、 2022-02-25 15:48 270阅读 0赞

本文实现了对二叉树的递归遍历和非递归遍历，当然还包括了一些栈操作。

二叉树的遍历本质上其实就是入栈出栈的问题，递归算法简单且容易理解，但是效率始终是个问题。非递归算法可以清楚的知道每步实现的细节，但是乍一看不想递归算法那么好理解，各有各的好处吧。接下来根据下图讲讲树的遍历。

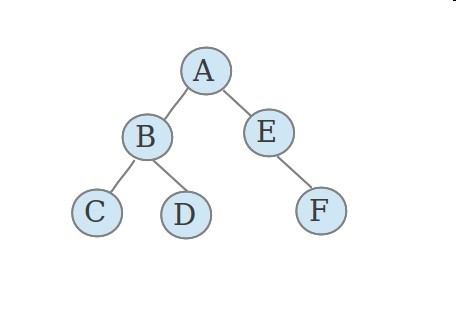
![20130507202022904][]

1、先序遍历：先序遍历是先输出根节点，再输出左子树，最后输出右子树。上图的先序遍历结果就是：ABCDEF

2、中序遍历：中序遍历是先输出左子树，再输出根节点，最后输出右子树。上图的中序遍历结果就是：CBDAEF

3、后序遍历：后序遍历是先输出左子树，再输出右子树，最后输出根节点。上图的后序遍历结果就是：CDBFEA

其中，**后序遍历的非递归算法**是最复杂的，我用了一个标识符isOut来表明是否需要弹出打印。因为只有当节点的左右子树都打印后该节点 才能弹出栈打印，所以标识isOut为1时打印，isOut初始值为0，这主要是为了处理非叶子节点。由后序遍历的原理决定，左右子树都被打印该节点才能打印，所以该节点肯定会被访问2次，第一次的时候不要打印，第二次打印完右子树的时候打印。叶子节点打印完后将isOut置为1。（纯粹是自己想的，应该还有逻辑更简单的算法）

isOut处理具体如下：

*  所有节点入栈的时候初始化为0；
 *  叶子节点打印输出后将isOut置为1；
 *  非叶子节点分两种情况。如果存在左子树，则输出左子树后将isOut置为1，此时指针已获得其右子树节点；如果不存在左子树，则将isOut置为1，此时指针已获得其右子树节点；在代码中分别体现在 if ( (p->lchild) && (p->lchild->isOut == 1) ) \{//如果存在左子树,并且左子树已经遍历完，则说明该节点已经入栈，不用再次Push,直接走向右子树  
    p->isOut = 1;  
    p = p->rchild;  
    \}和 if (!StackEmpty(s))  
    \{  
    GetTop(s,p);  
    if ( p->lchild == NULL )  
    p->isOut = 1; //右子树已输出，将父节点isOut置1  
    \}；
 *  遇到isOut=1的时候，说明左右子树都已输出，所以该节点也出栈打印出来。

以中序遍历为例，看看栈的内容是如何变化的：

![20130507203551093][]

具体的代码实现如下：

#include<stdio.h>
    #include<stdlib.h>
    
    #define STACKINITSIZE 100
    #define STACKINCREASESIZE 20
    
    typedef char ElemType;
    //树结构
    typedef struct tree
    {
        ElemType data;
        struct tree * lchild;
        struct tree * rchild;
        unsigned int isOut;   //专为后序遍历设置的，0为不需要被输出，1为需要被输出
    }TreeNode,*Tree;
    
    //栈结构
    typedef struct stack
    {
        Tree * base;
        Tree * top;
        int stacksize;
    }Sqstack;
    
    
    /*****************栈的操作声明********************/
    
    //初始化栈
    void InitStack( Sqstack &s );
    //元素入栈
    void Push( Sqstack &s, Tree e );
    //获得栈顶元素
    void GetTop( Sqstack s, Tree &e );
    //弹出栈顶元素
    void Pop( Sqstack &s, Tree &e );
    //判断栈是否为空，为空返回1，否则返回0
    int StackEmpty( Sqstack s );
    
    /*****************栈的操作声明********************/
    
    
    /*****************树的操作声明********************/
    //创建树,以先序序列建立树
    void CreateTree(Tree &t);
    //递归先序遍历
    void PreOrder(Tree t);
    //非递归先序遍历
    void PreOrder1(Tree t);
    //递归中序遍历
    void InOrder(Tree t);
    //非递归中序遍历
    void InOrder1(Tree t);
    //递归后序遍历
    void PostOrder(Tree t);
    //非递归后序遍历
    void PostOrder1(Tree t);
    /*****************树的操作声明********************/
    
    int main()
    {
        Tree T;
        printf("\n按先序序列输入结点序列，'#'代表空：");
        CreateTree(T);
    
        printf("\n非递归先序遍历的结果：");
        PreOrder1(T);
        printf("\n递归先序遍历的结果：  ");
        PreOrder(T);
    
        printf("\n非递归中序遍历的结果：");
        InOrder1(T);
        printf("\n递归中序遍历的结果：  ");
        InOrder(T);
    
        printf("\n非递归后序遍历的结果：");
        PostOrder1(T);
        printf("\n递归后序遍历的结果：  ");
        PostOrder(T);
        printf("\n");
    
    }
    
    
    /*****************栈的操作定义********************/
    
    //初始化栈
    void InitStack( Sqstack &s )
    {
        s.base = (Tree *)malloc(STACKINITSIZE*sizeof(Tree));
        if ( !s.base )
        {
        printf("InitStack内存分配出错\n");
        }    
        s.top = s.base;
        s.stacksize = STACKINITSIZE;
    }
    
    //元素入栈
    void Push( Sqstack &s, Tree e )
    {
        if ( s.top - s.base >= s.stacksize )
        {
        s.base = (Tree *)realloc(s.base,(s.stacksize+STACKINCREASESIZE)*sizeof(Tree));
        if ( !s.base )
            {
            printf("Push内存分配出错\n");
            return ;
            }
        
         s.top = s.base + s.stacksize;
        s.stacksize += STACKINCREASESIZE;
        }
        e->isOut = 0;
        *s.top++ = e;
    }
    
    //获得栈顶元素
    void GetTop( Sqstack s, Tree &e )
    {
        e = *(s.top - 1);
    }
    
    //弹出栈顶元素
    void Pop( Sqstack &s, Tree &e )
    {
        if ( s.top == s.base )
        {
        printf("栈为空\n");
        return ;
        }
        e = *(--s.top);
    }
    
    //判断栈是否为空，为空返回1，否则返回0
    int StackEmpty( Sqstack s )
    {
        if ( s.top == s.base )
        return 1;
        return 0;
    }
    
    /*****************栈的操作定义********************/
    
    
    
    /*****************树的操作定义********************/
    //创建树,以先序序列建立树
    void CreateTree(Tree &t)
    {
        char ch;
        scanf("%c",&ch);
        if ( ch == '#' )
        t = NULL;
        else
        {
        t = (Tree)malloc(sizeof(TreeNode));
            if ( !t )
        {
            printf("分配内存出错！");
            return ;
        }
        t->data = ch;
        CreateTree(t->lchild);
        CreateTree(t->rchild);
        }
    }
    
    
    //递归先序遍历
    void PreOrder(Tree t)
    {
        if ( t )
        {
        printf("%c",t->data);
        PreOrder(t->lchild);
        PreOrder(t->rchild);
        }
    }
    
    //非递归先序遍历
    void PreOrder1(Tree t)
    {
        Tree p = t;
        Sqstack s;
        InitStack(s);
    
        while ( p || !StackEmpty(s) )
        {
        if ( p )
        {
            printf("%c",p->data);
            Push(s,p);
            p = p->lchild;    
        }
        else
        {
            Pop(s,p); 
            p = p->rchild;
        }
        }
    
    }
    
    
    //递归中序遍历
    void InOrder(Tree t)
    {
        if ( t )
        {
        InOrder(t->lchild);
        printf("%c",t->data);
        InOrder(t->rchild);
        }
    }
    
    
    //非递归中序遍历
    void InOrder1(Tree t)
    {
        Tree p = t;
        Sqstack s;
        InitStack(s);  
        
        while ( p || !StackEmpty(s) )
        {
        if ( p )
            {
            Push(s,p);
            p = p->lchild;
        }    
        else
        {
            Pop(s,p);
            printf("%c",p->data);
            p = p->rchild;
        } 
        }
    }
    
    //递归后序遍历
    void PostOrder(Tree t)
    {
        if ( t )
        {
        PostOrder(t->lchild);
         PostOrder(t->rchild);
        printf("%c",t->data);
        }
    }
    
    
    //非递归后序遍历
    void PostOrder1(Tree t)
    {
        t->isOut = 0;
        Tree p = t;
        Sqstack s;
        InitStack(s); 
    
        while ( p || !StackEmpty(s) )
        {
        if ( p )
            {
            if ( p->isOut )
                {//左右子树都已输出，则该节点也输出        
                Pop(s,p);
                printf("%c",p->data);
            if (!StackEmpty(s))
                    GetTop(s,p); //得到弹出节点元素的父节点
                else
                p = NULL;
            }
            else
            {    
                if ( (p->lchild) && (p->lchild->isOut == 1) )
                {//如果存在左子树,并且左子树已经遍历完，则说明该节点已经入栈，不用再次Push,直接走向右子树          
                p->isOut = 1;
                p = p->rchild;   
                  }
                else
                {
                Push(s,p);
                p = p->lchild;
                }          
            }
            }
            else
            {
            if (!StackEmpty(s))
                GetTop(s,p); 
            else
            p = NULL;
    
            if ( p->rchild )
            {
                p = p->rchild;
            }
            else
            {
               Pop(s,p);
                printf("%c",p->data);
                p->isOut = 1;
                if (!StackEmpty(s))
                {
                GetTop(s,p);
                if ( p->lchild == NULL )
                    p->isOut = 1; //右子树已输出，将父节点isOut置1
            }
                else
                p = NULL;
            }
            
            }
        }
        
    }

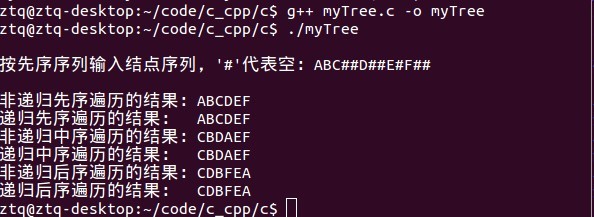
运行结果如下：

![20130508220440152][]

[20130507202022904]: /images/20220225/bf34b404f0a5471483152868c6462f3e.png
[20130507203551093]: /images/20220225/b55e7a2d4b3d4443b67f2d149046fcd6.png
[20130508220440152]: /images/20220225/1f21c564122141db9443ff1403f2b137.png