动态规划最长递增子序列-蒲公英云

动态规划最长递增子序列

小咪咪 2021-10-01 09:00 426阅读 0赞

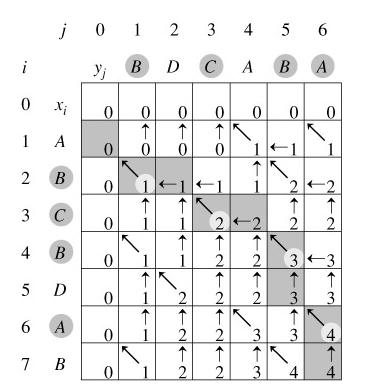
方法一：最长公共子序列法

将问题转换成求递增排序的数组与原数组的最长公共子序列。
不知道如何排序？看这里：七大排序算法总结
不知道什么是最长公共子序列？看这里: 最长公共子序列问题总结

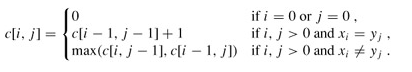
方法二：动态规划法

通过递推思路解决问题。要求长度为i的序列的Ai{a1,a2,……,ai}最长递增子序列，需要先求出序列Ai-1{a1,a2,……,ai-1}中以各元素(a1,a2,……,ai-1)作为最大元素的最长递增序列，然后把所有这些递增序列与ai比较，如果某个长度为m序列的末尾元素aj(j<i)比ai要小，则将元素ai加入这个递增子序列，得到一个新的长度为m+1的新序列，否则其长度不变，将处理后的所有i个序列的长度进行比较，其中最长的序列就是所求的最长递增子序列。

lis数组存储各元素作为最大元素的最长递增序列长度
pre前驱元素数组，记录当前以该元素作为最大元素的递增序列中该元素的前驱节点

import java.util.Stack;
public class test03231626 {
    public static int lis(int [] array)
    {
        int []lis = new int[array.length];
        int[] pre=new int[array.length];
        for(int i =0;i<array.length;i++)
        {
            lis[i]=1;
            pre[i]=i;
        }
         for (int j=1; j<array.length; j++) {  
                for (int i=0; i<j; i++) {  
                    if (array[j]>array[i] && lis[j]<lis[i]+1){ //注意array[j]<array[i]+1这个条件，不能省略。  
                        lis[j] = lis[i] + 1; //计算以array[j]结尾的序列的最长递增子序列长度  
                        pre[j]=i;
                    }  
                }  
            }  
        int max=0,index = 0;
        for(int k=0;k<lis.length;k++)
        {
            if(lis[k]>max){
                max=lis[k];
                index=k;
            }
        }
        System.out.println("最长递增子序列长度："+max);
        Stack<Integer> stack=new Stack<Integer>();  
        while(index!=pre[index]){
            //System.out.print(array[index]+" ");   
            stack.push(array[index]);
            index=pre[index];       
        }
        if(index==pre[index])
        //  System.out.print(array[index]+" ");
            stack.push(array[index]);
        while(!stack.isEmpty())
            System.out.print(stack.pop()+" ");          
        return max;
    }
    public static void main(String[] args){
        int[] array={35, 36, 39, 3, 15, 27, 6, 42};
        lis(array);
    }
}